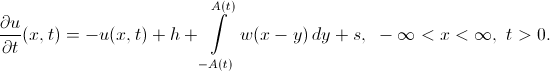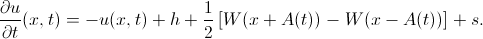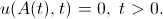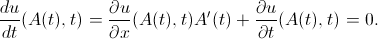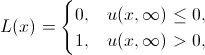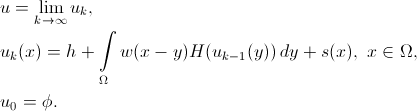この記事では、迷路を生成する1つの珍しいアプローチについて説明します。 これは、大脳皮質のAmaryニューロン活動のモデルに基づいています。大脳皮質は、ニューラルネットワークの連続的な類似体です。 特定の条件下では、写真に示すような非常に複雑な形状の美しい迷路を作成できます。
この記事では、迷路を生成する1つの珍しいアプローチについて説明します。 これは、大脳皮質のAmaryニューロン活動のモデルに基づいています。大脳皮質は、ニューラルネットワークの連続的な類似体です。 特定の条件下では、写真に示すような非常に複雑な形状の美しい迷路を作成できます。
多くの分析といくつかのプライベートデリバティブがあります。 コードが添付されています。
カットをお願いします!
はじめに
読者の多くは、すでに何らかの形で迷路を生成する問題に直面しており、頂点が迷路のセルであり、エッジが隣接するセル間の通路を表すグラフで最小スパニングツリーを見つけるためにPrimaおよびKruskalアルゴリズムを使用して解決されることが多いことを知っています。 私たちはグラフ理論から...計算神経生物学に向けて大胆な一歩を踏み出します。
20世紀の間に、科学者は単一のニューロン(神経系の細胞)とその相互作用の数学モデルを構築しました。 1975年、S。アマリは大脳皮質の連続モデルの光を紹介しました。 その中で、神経系は連続した媒体とみなされ、その各点には「ニューロン」があり、その膜の電位によって特徴付けられ、隣接するニューロンおよび外部刺激と電荷を交換することによって電位を変化させます。 アマリのモデルは、人間の視覚の多くの現象、特に精神活性物質によって引き起こされる幻視を説明することで有名です。
Amariのモデルは、最も単純な形式で、1つの積分微分方程式のコーシー問題です。
ここでは説明なしで行うことはできません:
 その時点でのニューロンの膜の電位の実際の値です
その時点でのニューロンの膜の電位の実際の値です  時間に
時間に  。
。 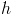 -残りの可能性(実際の定数)。
-残りの可能性(実際の定数)。 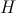 -ヘビサイドステップ関数:
-ヘビサイドステップ関数: 
 -重み関数。
-重み関数。  -外的刺激物。
-外的刺激物。  -最初の瞬間の電位の分布。
-最初の瞬間の電位の分布。  -領域の任意の点
-領域の任意の点  電位が決定されます。 迷路の2次元画像を生成する予定なので、
電位が決定されます。 迷路の2次元画像を生成する予定なので、  実際の平面全体を考慮します。
実際の平面全体を考慮します。 - プライベートデリバティブ
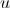 左側の時間的には、電位の瞬間的な変化を示します
左側の時間的には、電位の瞬間的な変化を示します 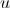 。 右側の部分は、この変更のルールを設定します。
。 右側の部分は、この変更のルールを設定します。 - 右側の最初の2つの用語は、刺激がない場合、電位値が安静時電位の値になる傾向があることを意味します。
- 次の用語は、隣接するニューロンの影響を考慮しています。 ヘビサイド関数は、ニューロンの活性化機能の役割を果たします。ニューロンは、電位がゼロよりも大きい場合にのみ、近傍に影響を与え始めます。 このようなニューロンをさらにアクティブと呼び、正のポテンシャルを持つポイントのセットをアクティビティのエリアと呼びます。 安静時ニューロンがアクティブであってはならないこと、つまり、安静電位が正であってはならないことは明らかです。 アクティブな隣人は、興奮性と抑制性の2つのグループに分けることができます。 興奮性ニューロンは隣人の可能性を高め、抑制性ニューロンは減少します。 同時に、興奮剤は小さな近所で強力な活動の爆発を引き起こし、抑制的なものは大きな半径の近くで徐々に活動を消します。 この事実は、重み関数の選択に反映されています。
 「メキシカンハット」の形:
「メキシカンハット」の形: 
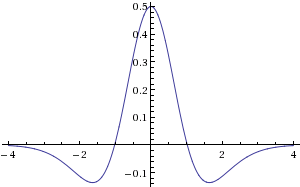
- 方程式の右側の最後の項では、外部刺激の作用が考慮されます。 たとえば、脳の視覚皮質の場合、自然な刺激は網膜から受信した信号です。 刺激は、非負の定常(時間独立)関数によって与えられると仮定します。
私たちは自分自身に質問します:モデルパラメータを選択することは可能ですか?
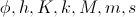 そのため、その定常解(
そのため、その定常解(  )迷路のイメージでしたか?
)迷路のイメージでしたか?
Amariモデルソリューションのプロパティ
Amariモデルの解を分析するには、1次元のケースの検討に限定するだけで十分です。 簡単にするために、
 行全体で一定です。
行全体で一定です。
まず第一に、いわゆるバンプソリューションに興味があります。 それらは、ある有限間隔でのみ正であるという点で注目に値します
 境界線を移動します。 それらのAmari方程式は次のように記述されます。
境界線を移動します。 それらのAmari方程式は次のように記述されます。 ソリューションの動作を理解するために、関数を紹介します
同じ方程式を次のように書き換えることができます。
バンプソリューションはアクティビティ間隔の境界で消滅することがわかっています(これが境界と呼ばれる理由です)。 この条件を正しい境界に記述します。
ここで、変数に関して最後のアイデンティティを区別します
 :
: ここから:
バンプ解の方程式の最後の式を
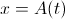 私達は得る:
私達は得る: ここで、に関する偏微分
 右側の境界の左側の解はゼロより大きく、右側の境界の解は小さいため、左側は常に負になります。 だから
右側の境界の左側の解はゼロより大きく、右側の境界の解は小さいため、左側は常に負になります。 だから したがって、境界のシフトの方向は、右側の式の値のみに依存します。 ゼロより大きい場合、アクティビティの領域が拡大し、小さい場合は縮小します。 ゼロの場合、平衡に達します。
可能な関数グラフを見てください。
 。
。
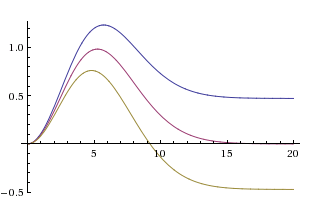
明らかに、次の2つのケースが考えられます。
- 限界値
 非負。 その後、バンプソリューションの活動領域は無限に拡大します。
非負。 その後、バンプソリューションの活動領域は無限に拡大します。 - 限界値
 否定的に。 そうすると、活動範囲が制限されます。 さらに、この場合、Amari方程式の解のアクティビティ領域の連結成分はマージされないことが示されます 。
否定的に。 そうすると、活動範囲が制限されます。 さらに、この場合、Amari方程式の解のアクティビティ領域の連結成分はマージされないことが示されます 。
残念ながら、2次元の場合、関数の明示的な式を取得します
 難しいので、評価するだけです。
難しいので、評価するだけです。 ここから:
迷路生成
必要な知識の荷物を集めたら、実際に迷路を生成するアルゴリズムを開始できます。
まず、「ラビリンス」というコンセプトそのものを決めましょう。 迷路とは、バイナリ関数を意味します
 そのようなエリア
そのようなエリア 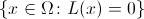 接続されています。 値0はフリーセルに対応し、値1は侵入不可能な壁に対応します。 接続の状態は、フリーセルから壁を破壊せずに他のセルに到達できることを示しています。 機能
接続されています。 値0はフリーセルに対応し、値1は侵入不可能な壁に対応します。 接続の状態は、フリーセルから壁を破壊せずに他のセルに到達できることを示しています。 機能  次の形式で検索します。
次の形式で検索します。 どこで
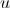 -アマリモデルの決定。 モデルのパラメータを決定するためだけに残ります。
-アマリモデルの決定。 モデルのパラメータを決定するためだけに残ります。
まず、任意の負の値を修正します
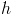 。 当然
。 当然 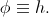 。 次に、関数を設定します
。 次に、関数を設定します  。 各ポイントでの値は、セグメント全体に均一に分布するランダム変数によって決定されます
。 各ポイントでの値は、セグメント全体に均一に分布するランダム変数によって決定されます  。 この場合、刺激はアクティビティを作成しません。 任意の正を修正します
。 この場合、刺激はアクティビティを作成しません。 任意の正を修正します  。 このパラメーターは、ポテンシャルの絶対値にのみ影響するため、重要ではありません。 任意の正を修正します
。 このパラメーターは、ポテンシャルの絶対値にのみ影響するため、重要ではありません。 任意の正を修正します 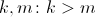 。 それらは、迷路の特徴的な壁の厚さを決定します。 パラメータ
。 それらは、迷路の特徴的な壁の厚さを決定します。 パラメータ  実験的に決定してから、前のセクションで取得した理論上の推定値と比較してください。
実験的に決定してから、前のセクションで取得した理論上の推定値と比較してください。
逐次近似法による定常解を求めます。
そして、これが待望のPythonのインタラクティブデモです。
import math import numpy import pygame from scipy.misc import imsave from scipy.ndimage.filters import gaussian_filter class AmariModel(object): def __init__(self, size): self.h = -0.1 self.k = 0.05 self.K = 0.125 self.m = 0.025 self.M = 0.065 self.stimulus = -self.h * numpy.random.random(size) self.activity = numpy.zeros(size) + self.h self.excitement = numpy.zeros(size) self.inhibition = numpy.zeros(size) def stimulate(self): self.activity[:, :] = self.activity > 0 sigma = 1 / math.sqrt(2 * self.k) gaussian_filter(self.activity, sigma, 0, self.excitement, "wrap") self.excitement *= self.K * math.pi / self.k sigma = 1 / math.sqrt(2 * self.m) gaussian_filter(self.activity, sigma, 0, self.inhibition, "wrap") self.inhibition *= self.M * math.pi / self.m self.activity[:, :] = self.h self.activity[:, :] += self.excitement self.activity[:, :] -= self.inhibition self.activity[:, :] += self.stimulus class AmariMazeGenerator(object): def __init__(self, size): self.model = AmariModel(size) pygame.init() self.display = pygame.display.set_mode(size, 0) pygame.display.set_caption("Amari Maze Generator") def run(self): pixels = pygame.surfarray.pixels3d(self.display) index = 0 running = True while running: self.model.stimulate() pixels[:, :, :] = (255 * (self.model.activity > 0))[:, :, None] pygame.display.flip() for event in pygame.event.get(): if event.type == pygame.QUIT: running = False elif event.type == pygame.KEYDOWN: if event.key == pygame.K_ESCAPE: running = False elif event.key == pygame.K_s: imsave("{0:04d}.png".format(index), pixels[:, :, 0]) index = index + 1 elif event.type == pygame.MOUSEBUTTONDOWN: position = pygame.mouse.get_pos() self.model.activity[position] = 1 pygame.quit() def main(): generator = AmariMazeGenerator((512, 512)) generator.run() if __name__ == "__main__": main()
コメントは不要だと思います。 重み関数を使用した畳み込みはガウスフィルターを介して計算され、画像は定期的に平面全体に継続することに注意してください(「ラップ」パラメーター)。 デモンストレーションは、クリックすることで任意の時点で積極的にポジティブポテンシャルを確立できるという意味でインタラクティブです。
予想されるソリューションの動作は、パラメーターの選択に依存します
 :
:
 |  |  |
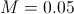 |  | 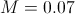 |
ここで、パラメーターの最適値の理論的推定値を取得します
 。 次の条件を満たす。
。 次の条件を満たす。 したがって、次のように推定できます。
悪くはないが、本当の意味
 理論上の見積もりよりわずかに高い。 これは設定することで簡単に確認できます
理論上の見積もりよりわずかに高い。 これは設定することで簡単に確認できます 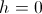 。
。
最後に、パラメータの値を変更することにより、迷路の「まばらさ」の度合いを変更できます
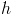 :
:
 |  |  |
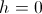 | 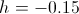 | 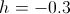 |
おわりに
それで、おそらく、迷宮を生成する最も異常な方法の議論を終えました。 この記事がおもしろいと思いました。 結論として、私は彼らの視野を広げたい人々のための参考文献のリストを提供します:
[1] Konstantin Doubrovinski、 ダイナミクス、安定性および分岐現象、皮質活動の非局所モデル 、2005年。
[2] Dequan Jin、Dong Liang、Jigen Peng、 動的ニューラルフィールドの定常解の存在と特性 、2011年。
[3] Stephen Coombes、Helmut Schmidt、Ingo Bojak、 Interface Dynamics in Planar Neural Field Models 、2012年。