大学での2年目に、私は、自分の意見では、そのような記事で私たち全員が知っている、よく知っている、または少なくともそれについて耳にするべきものの1つに会っただけです。 これは、(他の浮動小数点ソースで)浮動小数点数を表すための標準です。 IEEE-754標準という名前をどのようにして取得しましたか。
各IT専門家は少なくとも一度は浮動小数点数を聞いたことがあると思いますが、私にとって初めてこれは完全にナンセンスに思えました。 そして、それは簡単ではありません。結局、私たちが標準を研究した主題は「コンピューターアーキテクチャ」と呼ばれ、教師は現在の伝説です。 まあ、これはオフトピックです。
それでは、このIEEE-754標準とは正確には何ですか? 大学でロシア語の電子形式で与えられたとすぐに言いますが、Googleの30ページ目に到達しても、インターネットで見つけることはできませんでした。 著者が午前4時36分に書いた英語の例がありました。 私は、サタンが地球をゆっくりと引き継ぐことに決めたなら、彼がこの基準を作成すると言うサイトを見つけました。 しかし、それはあなたや私のような人々によって作成されました。
標準自体は、浮動小数点形式の数値を使用したバイナリ算術演算の説明です。 また、このような場合に発生する例外的な状況、この形式での記録などについても説明します。 当然、それを読んだ後、そしてそのような困難があっても、私は何も理解していませんでした! 結局、浮動小数点形式については何も知りませんでした。 しかし、これは失礼であり、任意の数の小数部分であり、知る必要があるのは精度だけです。
このテーマでは、大学でRGR(Settlement and Graphic Work)を計算しましたが、何らかの理由で、何かよりも多くの時間を費やす価値があることに気付きました。 これはおそらく私の研究のターニングポイントだった。 私は夜、この標準と特定のタスクについて、「連続ユニットのチェーンをゼロで置き換え、最も近い偶数に丸める、倍精度浮動小数点形式の2つの数値の除算」について説明しました。 それからそれは理解できませんでした。 そして、IEEE-754規格は常にこの割り当てに従っています。 実際、必要なものはすべてありました。
さて、IEEE-754規格について詳しく説明します。 それは、私がより詳細に説明したいいくつかの章を表します。
いつものように、すべては導入から始まります。 プログラムがあるという事実は、私が見たものよりもはるかに複雑です。 標準の作成の歴史について説明します。 結局のところ、プログラムはますます難しくなっており、デジタルコンピューターは古くなっており、新しいアーキテクチャに置き換える必要があります。 これが、70年代後半にIEEE(米国電気電子技術者協会)が多くの提案を考慮した委員会を設立した理由です。 委員会の作業の結果、IEEE 754標準«バイナリ浮動小数点演算≫(1985)が国際化されました。 その基礎は、バークレー大学ウィリアム・カハン大学の数学教授によって開発されました。
その後、IEEE 754-1985に基づいて次の標準が開発されました。
-IEEE 854-1987、10進数演算と2進数をカバー。
-IEC 60559-1989 IEC≪のバイナリ浮動小数点演算
マイクロプロセッサシステム≫(IEC-International Electrotechnical Commission)。
IEEE 754標準は義務ではありませんが、それに指定されている形式のパッケージの使用、データのエンコード方法、丸め結果などを推奨しています。 ユニバーサルコンピューターの設計者向けの形式を選択する作業は非常に簡素化され、その時点から、企業は標準の推奨事項を満たす浮動小数点演算を備えたユニバーサルコンピューターの生産を開始しました。 プログラマーのタスクもいくらか単純化されます。 さまざまなコンピューターの2進浮動小数点演算の機能を調べる必要はなく、標準の知識を習得するだけです。
しかし、標準は保守的であり、永遠ではないことを覚えておく必要があります。 それにもかかわらず、同僚全員がこの標準を使用しています。
この規格は、単精度(32ビット)、倍精度(64ビット)、および倍精度の2つの精度をサポートしています。 丸めエラーなどを防ぐために、他の形式も提供されます。 この規格では、Nan、無限大、ゼロ除算などの緊急事態のケースについて説明しています。 何にも似ていませんか? 浮動小数点形式の丸め数値は非常に重要な役割を果たします。 これも規格に記載されています。
最後に、メインセクション-浮動小数点形式の数値の操作を実行します。 このセクションでは、比較から除算までのすべての算術演算と、そのような演算を実行する際のすべてのニュアンスについて説明します。 このセクションについては、「一言で言えば」とは言えません。 これは本当の混乱であるとしか言えず、これがどのように起こるかを理解するという課題に直面しました。
「浮動小数点形式の除算」作業のアルゴリズムについて簡単に説明します。 オペランドAとBを受け取った後、例外的な状況の考えられるすべてのケースについてそれらをチェックする必要がありました。 これは、ゼロとナンと無限大による除算です。 少し下の表では、形式がサポートする数値の表現の種類が示されています。
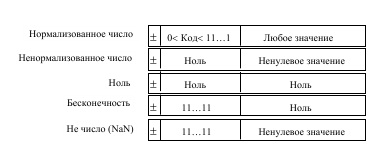
オペランドが実際にIEEE-754形式の数値であった場合、演算の2番目の段階である注文の変換が始まりました。 浮動小数点数が次のように見えることは秘密ではありません。

これは、数値の単精度表現です。
私の理解では、コンピューター内の番号の順序は、コンピューター内の番号のシリアル番号、つまりその順序です。 確かに科学的な定義がありますが、それはさらに混乱させるだけです。 そのため、番号の順序は異なるため、分割することはできません。 まず、注文を移動して注文を1つのフォームに移動します。 ただし、このためには、最小値と最大値の次数を分析する必要がありました。 そして、順序シフトが発生すると、仮数もシフトします。 順序が等しい場合、仮数、境界から飛び出したかどうか、ゼロで埋められたかどうかなどを確認する必要があります。 一連のチェックを完了した後、最も重要なことに進むことができます:最後に仮数を分割します。 さて、すべてのバイナリ演算のように、すべてが単純です。 除数を被除数で除算し、残りをレジスタに書き込んで追加しました。 分割する方法はまだいくつかあります:リカバリありと残りの復元なし。 それだけではありません! 最後に、目的の条件に従って結果を切り上げ、商の符号を決定する必要があります。
それはただの言葉ですが、恐ろしいように聞こえますが、実際はずっと良く見えます。 それから私は率直にこの基準に落ちました。それはデジタルコンピューターとバイナリー算術のより深い知識だけでなく、これを行うことができる喜び、私が非常に重要なことを知っていることに気づく喜びをもたらしました。
私にはすべてがあります。実際、このトピックは非常に興味深く、興味深いものです。 興味のある方は、IEEE-754規格を喜んで廃止し、ご質問にお答えします。
ありがとう