始めましょう!
タスク:平らな国とその中のn個の都市を考えます。 電話回線の合計の長さが最小限になるように、すべての都市を電話で接続する必要があります。
タスクの明確化。 タスクは、電話通信、つまり は、通信の推移性を意味します。i番目の都市がj番目に接続され、j番目の都市がk番目に接続されている場合。 また、電話回線は電話交換機でのみ分岐でき、クリーンなフィールドでは分岐できないことも理解されています。 最後に、最小値の要件(推移性とともに)は、目的のソリューションにサイクルがないことを意味します。
グラフ理論に関して 、Prima-Kraskal問題は次のとおりです。
n個の頂点を持つグラフが与えられます。 リブの長さが与えられます。 最小長のスパニングツリーを見つけます。
ご存じのように、n個の頂点を持つツリーにはn-1個のエッジがあります。 (サイクルがない限り)各エッジを貪欲に選択する必要があることがわかります。
Prima-Kraskalアルゴリズムの簡単な説明:ループでn-1回、「まだ選択されていない最短リブを選択します。ただし、既に選択されているものとループを形成しない場合」。
この方法で選択されたエッジは、目的のツリーを形成します。
問題を解決するために、エッジと頂点のリストとして表示されるグラフが作成されます。
スパニングツリー検索アルゴリズムは、次の手順に分割できます。
•エッジのリストを長さの昇順で並べ替えます。
•「貪欲な」アルゴリズムを適用し、エッジのリストを取得します。
•結果のエッジのリストがスパニングツリーであるかどうかを確認します。
欲張りアルゴリズムは次のように機能します。最小長の選択されていないエッジを選択する必要があります(エッジは、選択された他のエッジとサイクルを形成してはなりません)。
次に、 SWI-Prologでの結果のアルゴリズムの実装:
%
launch:-
write_ln(':'), read(X),
write_ln(' :'), read(Y),
city(X,Y,Z),
write_ln(' :'),
write(Z).
launch:-
write_ln(' ').
%
%
%Z1 - ,
%Y-
%Z2 -
minimum([],Z,Z):- !.
minimum([[X1,X2,_]|Y],Z1,Z2):-
not(search(X1,X2,Z1,[X1])),!,
minimum(Y,[[X1,X2]|Z1],Z2).
minimum([_|Y],Z1,Z2):- minimum(Y,Z1,Z2). %
% 1 2
% - 7.
%, Y - , Z - ( ).
search(X1,X2,Y,_):- member([X1,X2],Y).
search(X1,X2,Y,_):- member([X2,X1],Y).
search(X1,X2,Y,Z):- member([X1,X3],Y),
not(member(X3,Z)), search(X3,X2,Y,[X3|Z]).
search(X1,X2,Y,Z):- member([X3,X1],Y),
not(member(X3,Z)), search(X3,X2,Y,[X3|Z]).
% ( )
%
% L1 - , X - , L2 -
ins(X,[],[X]).
ins([X1,X2,R1],[[Y1,Y2,R2]|L],[[X1,X2,R1]|[[Y1,Y2,R2]|L]]):- R1<R2,!.
ins(X,[Y|L1],[Y|L2]):- ins(X,L1,L2).
%
%
%L - ,Y1 - , Y3 - .
sortrast([],Y,Y). sortrast([X|L],Y1,Y3):- ins(X,Y1,Y2), sortrast(L,Y2,Y3).
% .
%
%Z - X - , Y - ,
city([X|L],Y,Z):- sortrast(Y,[],Y1), minimum(Y1,[],Z), all(X,L,Z).
%
%
% x -, Z - L -
all(_,[],_).
all(X,[Y|L],Z):- search(X,Y,Z,[X]),!,all(X,L,Z).
次の述語がプログラムに実装されました。
• 起動 -画面に情報を表示するために使用されます。 たとえば、都市のリストとそれらの間の散布図。
• Sortrast (L1、L2、L3) -insertメソッドを使用してリストL1をソートします。L2は現在のリスト、L3は結果です。
• 市(X、Y、Z) -電話回線による都市の接続。ここで、X-都市のリスト、Y-距離のリスト、Z-結果。
• 検索(X1、X2、Y、Z )-頂点X1から頂点X2へのパスの検索を実装します。ここで、Yはエッジのリスト、Zは頂点のリスト(渡される)です。
• all(X、Y、Z) -都市の電話カバレッジをチェックします。 Xは最初の都市、Lは他の都市のリスト、Zは電話回線のリストです。
• ins(X、L1、L2) -述語は要素XをL1(エッジのソートされたリスト)に挿入します。 L2は結果です。
• 最小(Y、Z1、Z2) -最小(長さ)接続を見つけるための述語。 ここで、Yはエッジのリスト、Z1は選択されたエッジ、Z2は結果です。
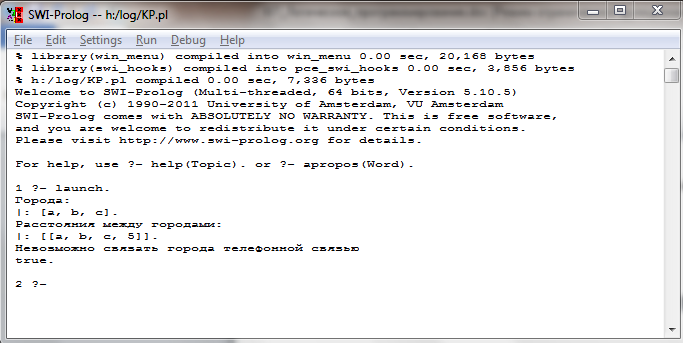
プログラムの結果: