In almost every card game after the game you need to shuffle the cards. While I am shuffling the cards, the question always arises in front of me: "Already enough?" This is a serious question - I don’t want to spend too much time, and playing on a charged deck is also not fun.

The article will deal with the situation.

Shuffle Way

There are cool ways to shuffle cards, riffle shuffle, for example.



I don’t know how, and cardboard cards cannot be shuffled like that, so I shuffle in a simple way, it looks something like this:



First, I separate the part from the deck, then I throw the share of this part to the other side, and then I report the remaining share. According to my observations, people shuffle cards this way or that way. In general, it can be divided into a larger number of parts, but these are already details. In the article we will analyze this shuffle method.

What is random card layout?

The first thing that occurred to me was that it’s a good layout, any card can be equally likely to be in the i-th place.

But this is not enough. For example, if you cut the deck — divide it into two in a random place and swap them — then the first card can be any chance. But at the same time, this is obviously a bad layout: after each card, except for a few, the same card will go that lay after it before the “cut”. That is, players will receive "correlated" cards. In the case of a fool, one will be beaten, and the other will be beaten, and this will not be accidental.

Another approach to determining a good layout is that at i + 1st place there is a card independent of the card at i-th place. You can imagine it this way: if you look at the top card of the deck, you can’t guess which card will be next.

This approach may also have problems that are solved by considering large joint distributions, but for the current analysis it is completely suitable for us.

How to measure the "goodness" of the layout

We took the deck left over from the previous game. We number all the cards in order. The bad situation is when after shuffling in some place after the card with number i there is a card with number i + 1. Therefore, we will measure the proportion of cards that are in order after shuffling.

def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

It’s clear that even in a well-shuffled deck, some cards will randomly fall in order. Their share will be on average 1 / (n-1), where n is the number of cards in the deck.

results

We calculate the probability of consecutive cards for a deck of 52 cards, depending on the number of mixing iterations.



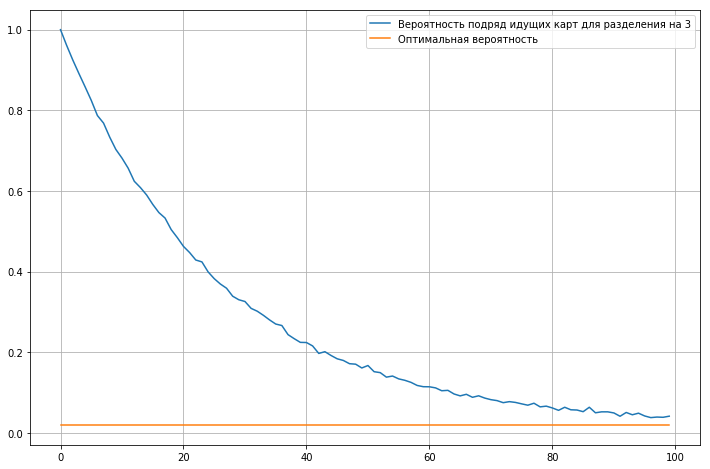
The graph shows that even after hundreds of iterations, the probability of consecutive cards is approximately two times higher than the ideal probability.

 import random def two_split_shuffle(a): s1 = random.randint(1,len(a)-1) s2 = random.randint(1,len(a)-1) s_min = min(s1, s2) s_max = max(s1, s2) p1 = a[:s_min] p2 = a[s_min:s_max] p3 = a[s_max:] return p3 + p2 + p1 def shuffle_n(a, f, n): for _ in range(n): a = f(a) return a def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total def expected(f, n = 100): s = 0 for _ in range(n): s += f() return s / n def get_expected_next_stat(shuf, n, cards): return expected(lambda: next_stat(shuffle_n(range(cards), shuf, n))) cards = 52 x = range(100) y = map(lambda i: get_expected_next_stat(two_split_shuffle, i, cards), x) import matplotlib.pyplot as plt %matplotlib inline plt.figure(figsize=(12,8)) plt.plot(x, y, label = u'       3') plt.plot(x, [1./(cards-1)] * len(x), label = u' ') plt.grid() plt.legend()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

In general, we can assume that 60 iterations is the optimal amount, less is definitely bad. I do about 16-17 iterations in 30 seconds. This means that for a normal shuffle it will take almost two minutes .

My friends and I never shuffle cards that much. And this means that our game is very much influenced by the balance of the last game.

Be careful)