ChipWhisperer: Energy Attack on Magma

Posted by rakf

As part of the Summer of Hack 2019 at Digital Security, I dealt with a power attack and worked with ChipWhisperer.

What is it?

Energy analysis is a type of attack through third-party channels. That is, attacks that use information that appears as a result of the physical implementation of the system.

What information may be useful to an attacker:

• cryptographic conversion time;
• power usage;
• electromagnetic fields;
• noise, etc.

An energy attack is considered the most universal.

Why does it work?

Microprocessors, microcontrollers, RAM, and many other logic circuits are based on CMOS technology. The power consumption of CMOS circuits consists of two components: static and dynamic. Static power consumption is very small, which is one of the reasons for the monopolization of technology. The dynamic power is due to the switching of transistors and depends on the processed data and the operations performed. Since the static component is mainly constant, the change in the total power is due exclusively to dynamic power and, therefore, the total energy consumption can be used for analysis.

Tools

ChipWhisperer , I used the 2-part version:

ChipWhisperer is an open source toolkit for researching the security of embedded devices. It allows energy analysis and error-based attacks.

The fee will cost $ 250. Developers position it as a revolutionary solution, because such complexes, according to the creators, cost from $ 30k. The device consists of 2 boards: target and capture board.

There are other versions, with their advantages (but also at a great cost), you can also separately purchase various target boards, expansion cards, probe for a full analysis of your devices and use ChipWhisperer only for removal.

ChipWhisperer has an excellent wiki , small development labs , and by the 5th version they even made good API documentation . Tracks are removed from the connected device using their software and recorded as a NumPy array.

First you need to write the firmware for the target device. As part of the lab, the ciphers AES, DES, TEA are considered. For them, there are already ready-made firmware and settings for removing traces (the number of samples to be taken, offset, ADC frequency, etc.). For independent research settings will have to be selected experimentally.

As mentioned above, you can provoke a failure of the target board: causing a malfunction of the clock signal, skip instructions and extract secret information.

In large complexes, an oscilloscope is used to take tracks.

Analysis

There are several basic analysis methods:

• simple power analysis (SPA);
• differential power analysis (DPA);
• power correlation analysis (CPA).

A simple power analysis includes a visual analysis of the power graph. For example, a password can be obtained one character at a time by observing the power profile when the correct character is entered and comparing with the wrong one.

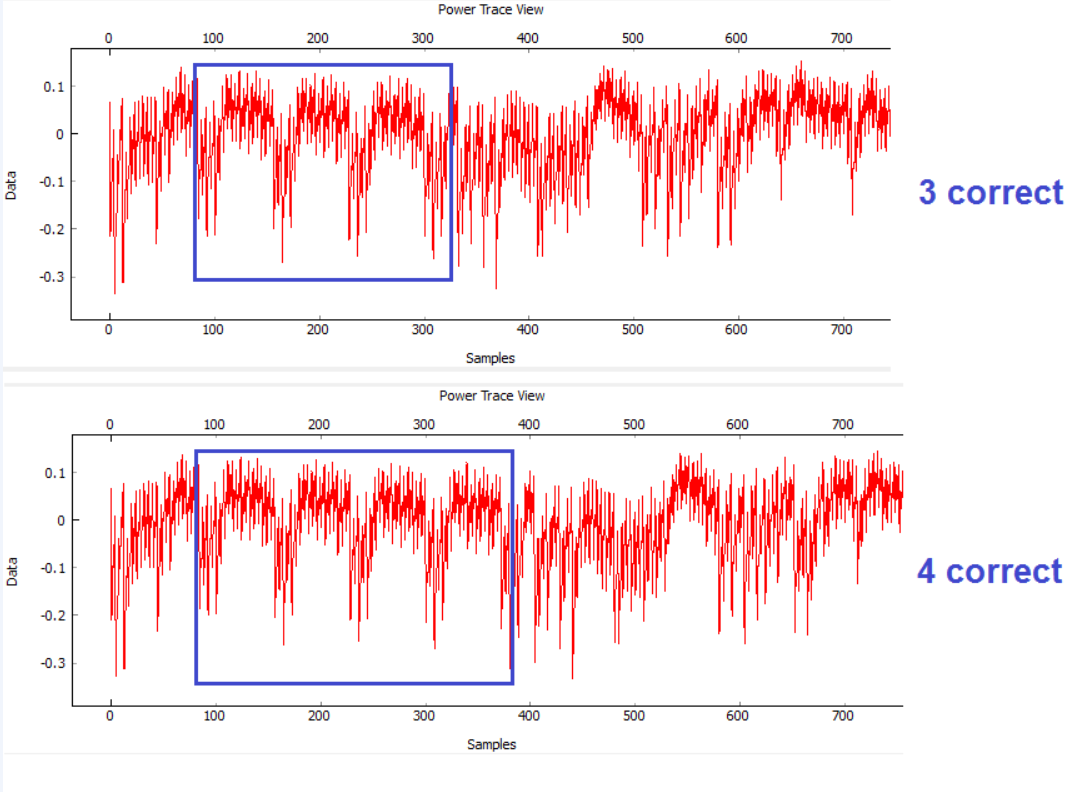
Or you can see encryption rounds on the tracks. There is little data to obtain a key, but it can be assumed which algorithm is being executed. The figure clearly shows 10 rounds of AES.

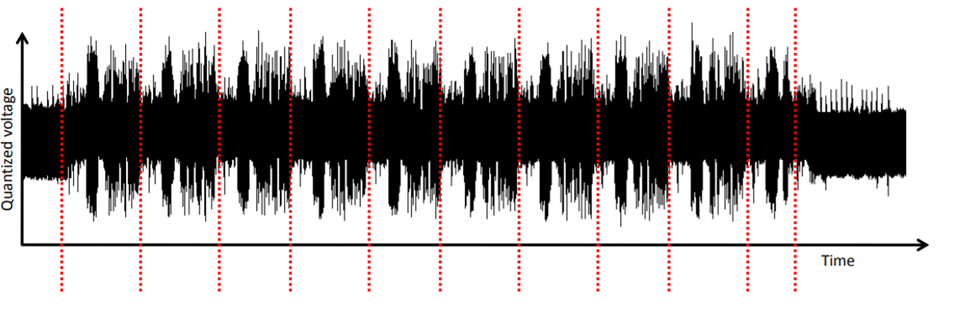
Differential analysis (DPA) is much more efficient than simple analysis. DPA is based on statistical analysis methods to detect differences in power traces. A very effective tool, however, to “open” the key will require a large number of routes. I did not use this method for analysis, but in the end I will give some links to sources where it is well described.

The basis of correlation analysis is a statistical apparatus for determining the secret encryption key. Sometimes it is isolated in a separate type, sometimes referred to as DPA. This method requires fewer traces than DPA, I used it for power analysis. I’ll tell you more about it.

The main task is to build an accurate model of energy consumption of the device under study. If an accurate model is built, there is a noticeable correlation between the predicted and the actual value.

One of the power models that can be used is the Hamming weight model. Hamming's weight is the number of non-zero values ​​in binary representation. The assumption of this model is that the number of bits set in the register will correlate with the energy consumed by the device. Hamming’s weight itself is used hereafter as a conventional unit of energy. The Hamming distance model is also used - the number of different bits in 2 values.

To compare the Hamming weight model and real power consumption, a linear Pearson coefficient is used. It shows the linear dependence of one quantity on another. With a correctly constructed model, this coefficient will tend to 1.

The generalized CPA algorithm consists of the following main steps:

• remove power consumption when converting messages on an unknown key;
• we build a model of energy consumption of the chip when converting the same messages to all possible variants of the key sub-block (256 options for each byte);
• we find the linear correlation coefficient for the simulated power consumption and real. In the case of a true key, the coefficient will tend to 1;
• the algorithm is repeated for the remaining key sub-blocks.

As a result, the key is restored sequentially, in small parts. If we attack one byte of the key at a time, then we use 2 ⁸ attempts for each key. For example, if you pick AES - 128, then the total number of attempts for 16 bytes of the key will be 2 ¹² , which is much better than hitting 2 ¹²⁸ .

Magma cipher analysis

Magma is a code that is defined in GOST R 34.12-2015, in fact the same GOST 28147-89, only in profile. The encrypted block goes through 32 rounds in which some transformations occur. The key consists of 256 bits, each round key is a part of the original.

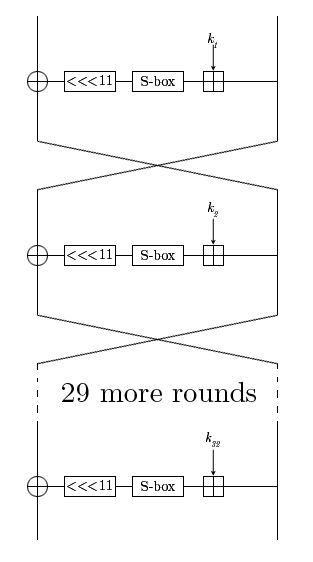
We will analyze the data obtained using the CPA method.

First you need to choose an intermediate value of the algorithm, which depends on the known data and a small part of the key and can be calculated by simple transformations. Usually this value is the S-box output (Magma now has 1 substitution table, so it’s easier to carry out such attacks) of the first (open texts are known) or the last round (ciphertexts are known).

I researched a key with well-known open texts, therefore this option will be considered further. In the Magma algorithm, in contrast to DES, AES, addition of a 32-bit block with a round key occurs modulo 2 ³² , therefore, it is better to start the analysis from the last outputs of the S-box, since adding the highest values ​​does not affect the younger ones. We consider the output of each S-box: first 8, then given 8, 7 and so on until the first. Track removal was carried out on an 8-bit microcontroller, and we can assume that it worked with dual S-boxes. Therefore, I will attack immediately by 1 byte.

Calculation of the energy model for the last key byte:

for kguess in range(0, 256): #Initialize arrays & variables to zero sumnum = np.zeros(numpoint) sumden1 = np.zeros(numpoint) sumden2 = np.zeros(numpoint) hyp = np.zeros(numtraces) for tnum in range(numtraces): hyp[tnum] = HW[leak("Gost28147_tc26_ParamZ", kguess, block2ns(text[tnum])[0], 0)]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

where the leak function simply returns the S-box output of the last byte.

We calculate the linear Pearson coefficient for the simulated and real values ​​according to the formula:

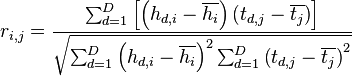
  cpaoutput = [0]*256 maxcpa = [0]*256 #Mean of hypothesis meanh = np.mean(hyp, dtype=np.float64) #Mean of all points in trace meant = np.mean(traces, axis=0, dtype=np.float64) #For each trace, do the following for tnum in range(0, numtraces): hdiff = (hyp[tnum] - meanh) tdiff = traces[tnum,:] - meant sumnum = sumnum + (hdiff*tdiff) sumden1 = sumden1 + hdiff*hdiff sumden2 = sumden2 + tdiff*tdiff cpaoutput[kguess] = sumnum / np.sqrt( sumden1 * sumden2 ) maxcpa[kguess] = max(abs(cpaoutput[kguess]))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

When choosing a true subkey, the correlation coefficient will have a significant surge:

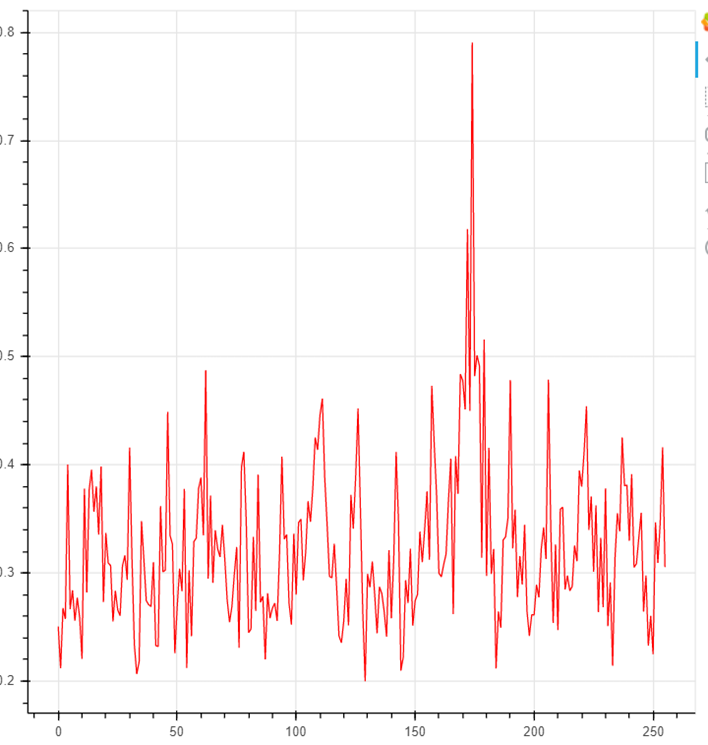
Thus, each byte of the round key is analyzed.

  for bnum in range(0, 4): cpaoutput = [0]*256 maxcpa = [0]*256 for kguess in range(0, 256): best_round_key = kguess << (bnum * 8) | best_round ...
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Given the first round key, we can calculate the 2 and subsequent round keys in the same way. A full Magma key can be obtained by taking out 8 round keys.

In the process of solving this problem, several nuances arise. Unlike AES, DES, Grasshopper ciphers, addition of a plaintext round key occurs modulo 2 ³² . The addition of low bits affects the high, unlike XORa. When calculating each subsequent subkey, you have to consider the results of the past. Similarly with round keys. The data is very sensitive. If one of the values ​​is incorrectly calculated, further calculation of the entire key will be incorrect.

It is also worth considering that it is now quite difficult to find a chip that has a four-bit architecture: most of the chips have eight-bit. Of course, there are specialized cryptographic chips that are designed for a specific security conversion algorithm (or several algorithms) and have the most efficient architecture.

To execute the DES cipher, such a cryptoprocessor can have a six-bit architecture, for Magma - a four-bit one, which allows each S-box to be processed separately. My target device is 8-bit, and in the case of “Magma”, conversion will be performed on eight bits in one approach, i.e. replacement will take place on 2 S-box, power consumption will be considered for 2 S-box. If one of the S-boxes, senior or junior, matches the true key, and the other does not match, high correlation bursts may occur.

Given all of the above, at the output we have the following script for analyzing energy consumption paths for the Magma cipher:

  import numpy as np path = r'C:\Users\user\chipwhisperer\projects\gost_10000_2_data\traces\2019.08.11-19.53.25_' traces = np.load(path + 'traces.npy') text = np.load(path + 'textin.npy') keys = np.load(path + 'keylist.npy') HW = [bin(n).count("1") for n in range(0,256)] SBOXES = {"Gost28147_tc26_ParamZ": ( (12, 4, 6, 2, 10, 5, 11, 9, 14, 8, 13, 7, 0, 3, 15, 1), (6, 8, 2, 3, 9, 10, 5, 12, 1, 14, 4, 7, 11, 13, 0, 15), (11, 3, 5, 8, 2, 15, 10, 13, 14, 1, 7, 4, 12, 9, 6, 0), (12, 8, 2, 1, 13, 4, 15, 6, 7, 0, 10, 5, 3, 14, 9, 11), (7, 15, 5, 10, 8, 1, 6, 13, 0, 9, 3, 14, 11, 4, 2, 12), (5, 13, 15, 6, 9, 2, 12, 10, 11, 7, 8, 1, 4, 3, 14, 0), (8, 14, 2, 5, 6, 9, 1, 12, 15, 4, 11, 0, 13, 10, 3, 7), (1, 7, 14, 13, 0, 5, 8, 3, 4, 15, 10, 6, 9, 12, 11, 2), )} def _K(s, _in): """ S-box substitution :param s: S-box :param _in: 32-bit word :returns: substituted 32-bit word """ return ( (s[0][(_in >> 0) & 0x0F] << 0) + (s[1][(_in >> 4) & 0x0F] << 4) + (s[2][(_in >> 8) & 0x0F] << 8) + (s[3][(_in >> 12) & 0x0F] << 12) + (s[4][(_in >> 16) & 0x0F] << 16) + (s[5][(_in >> 20) & 0x0F] << 20) + (s[6][(_in >> 24) & 0x0F] << 24) + (s[7][(_in >> 28) & 0x0F] << 28) ) def block2ns(data): """ Convert block to N1 and N2 integers """ data = bytearray(data) return ( data[7] | data[6] << 8 | data[5] << 16 | data[4] << 24, data[3] | data[2] << 8 | data[1] << 16 | data[0] << 24, ) def addmod(x, y, mod=2 ** 32): """ Modulo adding of two integers """ r = x + int(y) return r if r < mod else r - mod def _shift11(x): """ 11-bit cyclic shift """ return ((x << 11) & (2 ** 32 - 1)) | ((x >> (32 - 11)) & (2 ** 32 - 1)) def round(sbox, key, data, byte): s = SBOXES[sbox] _in = addmod(data, key) sbox_leak = _K(s, _in); return (sbox_leak >> (8 * byte)) & 0xFF def Feistel(sbox, key, data, nround): s = SBOXES[sbox] w = bytearray(key) x = [ w[3 + i * 4] | w[2 + i * 4] << 8 | w[1 + i * 4] << 16 | w[0 + i * 4] << 24 for i in range(8) ] n1, n2 = block2ns(data) for i in range(nround): n1, n2 = _shift11(_K(s, addmod(n1, x[i]))) ^ n2, n1 return n1 numtraces = len(traces) numpoint = np.shape(traces)[1] bestguess = [0]*32 round_data = [0] * numtraces for i in range(numtraces): round_data[i] = [0] * 8 for rnum in range(0, 8): best_round = 0 for tnum_r in range(numtraces): round_data[tnum_r][rnum] = Feistel("Gost28147_tc26_ParamZ", bestguess, text[tnum_r], rnum) for bnum in range(0, 4): cpaoutput = [0]*256 maxcpa = [0]*256 for kguess in range(0, 256): #Initialize arrays & variables to zero best_round_key = kguess << (bnum * 8) | best_round sumnum = np.zeros(numpoint) sumden1 = np.zeros(numpoint) sumden2 = np.zeros(numpoint) hyp = np.zeros(numtraces) for tnum in range(numtraces): hyp[tnum] = HW[round("Gost28147_tc26_ParamZ", best_round_key, round_data[tnum][rnum], bnum)] #Mean of hypothesis meanh = np.mean(hyp, dtype=np.float64) #Mean of all points in trace meant = np.mean(traces, axis=0, dtype=np.float64) #For each trace, do the following for tnum in range(0, numtraces): hdiff = (hyp[tnum] - meanh) tdiff = traces[tnum,:] - meant sumnum = sumnum + (hdiff*tdiff) sumden1 = sumden1 + hdiff*hdiff sumden2 = sumden2 + tdiff*tdiff cpaoutput[kguess] = sumnum / np.sqrt( sumden1 * sumden2 ) maxcpa[kguess] = max(abs(cpaoutput[kguess])) best_round = best_round | (np.argmax(maxcpa) << (bnum * 8)) bestguess[((rnum + 1) * 4)-bnum - 1] = np.argmax(maxcpa) print "Best Key Guess: " for b in bestguess: print "%02x "%b,
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

GitHub Results Repository

conclusions

As part of the study, I worked with ChipWhisperer. Despite the fact that I have not tried all the tools (for example, glitching), I definitely find ChipWhisperer useful, especially if you do not want to buy expensive special hardware.

As for the analysis of our cipher for energy consumption, it is more resistant to this attack than the ciphers described above, but with enough data, the key can be obtained without problems.

Interesting materials:

• P. Kocher Differential Power Analysis
• "Power Analysis Attacks: Revealing the Secrets of Smart Cards"
• Cryptography at gunpoint I: looking for keys of cryptographic algorithms R. Korkikyan.
• Cryptography at gunpoint II: differential nutrition analysis R. Korkikyan.
• Report with ZeroNights 2014 R. Korkikyan.
• cryptocoding v2 with ZeroNights 2014 about software implementation.