A couple of warnings to the reader:
In order to (as much as possible) simplify the process of explanation and squeeze the volume of publication, it is worth immediately making a key reservation - everything that we write about the practical side of the issue is correct for the TLS protocol version 1.3. This means that although your ECDSA certificate will, if desired, work with TLS 1.2, the description of the handshake process, cipher suites and benchmarks is made based on the latest version of the TLS protocol - 1.3. As you understand, this does not apply to the mathematical description of the algorithms that underlie the foundation of modern cryptographic systems.
This material was not written by a mathematician or even an engineer - although they helped to pave the path through the math of math. Many thanks to the staff of Qrator Labs.
( E lliptic C urve) D iffie- H ellman ( E phemeral)
21st Century Diffie-Hellman Legacy
Naturally, this topic does not begin with Whitfield Diffie and not with Martin Hellman. Alan Turing and Claude Shannon made a huge contribution to the theory of algorithms and information theory, as well as to the field of cryptanalysis. Diffie and Hellman, in turn, are officially recognized by the authors of the idea of public-key cryptography (also called asymmetric) - although it is now known that serious results in this area have also been achieved in the UK. However, they remained classified for a long time - which makes the two gentlemen mentioned in the subtitle pioneers.
What exactly?
This may seem funny, but until November 6, 1976, there was no available knowledge regarding public-key cryptographic systems. Whitfield Diffie and Martin Hellman (and, in fact, Ralph Merkle) - mathematicians, computer engineers and enthusiasts, as well as cryptologists were the first to propose a suitable concept.
During World War II, cryptography helped to keep information secret, and cryptanalysis helped to disclose it. The United States and the United Kingdom considered themselves the most advanced in the field of cryptography. These two countries included cryptographic algorithms in the arms section and vetoed their exports. At the same time, encryption available and intended for commercial or home use has been loosened in these countries. For this reason, British researchers who worked on an asymmetric key distribution scheme at the Government Communications Center (GCHQ) and developed a similar concept were not recognized by the community until 1997, when the existing restrictions on cryptographic algorithms and their description lost all meaning and, by and large morally outdated.
Coming back to our pair of inventors - what exactly did Diffie and Hellman revolutionize?
To explain this, let's take a look at the illustration from the original publication, which perfectly reflects the giant leap in understanding how cryptography can work - even if initially only theoretically:
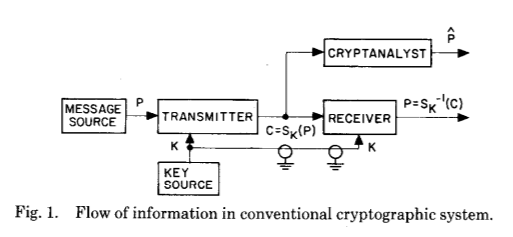
And now for the following:
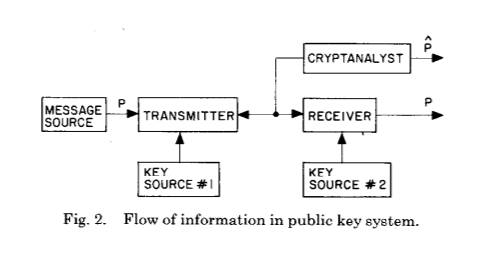
These two pictures show the main innovation of Whitfield Diffie and Martin Hellman after centuries of development of cryptography and cryptanalysis - the establishment of a common secret as a result of calculations of a certain type.
Let's look at another picture from Wikipedia, where different colors are used as secrets:
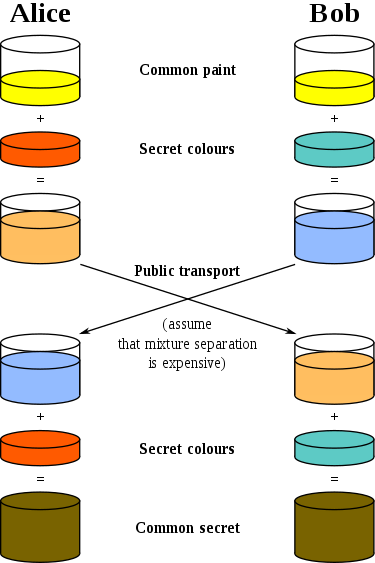
She also explains well what is happening. Before the Diffie and Hellman innovation, there was only one common key in the form of a common key establishment scheme - it was used to encrypt and decrypt a message. If you want to transfer such a key to the second side, it must be transmitted via an initially secure channel. Immediately all the limitations of such a scheme become clear - you need a secure (from listening) communication channel, you cannot use the same key more than once , and, ideally, the key length should correspond to the length of the message.
Claude Shannon, in his later declassified work, “Theory of Communication in Secret Systems,” proved that all theoretically unbreakable ciphers must have the same properties as a one-time cipher block — also known as the Vernam cipher, by the name of the creator of this additive polyalphabetic stream encryption algorithm.
And again, let's take a look at the original scientific publication:
Before we go any further, let's ask ourselves an obviously simple question - how could two, even very intellectually developed, people come up with something so breakthrough in the applied field, especially given the huge successes of wartime? Most likely due to the combination of the following areas that were actively developing then:
- Theory of Information Formulated by Claude Shannon;
- Algorithm theory , which was influenced, among others, by Alonzo Church, John von Neumann and Alan Turing;
- And, most of all, the theory of computability , based mainly on the work of Turing.
We can say that all these areas have developed and matured around the same period of the 20th century. Diffie and Hellman also mentioned Claude Shannon as a figure who influenced their work more than others.
The concept of “Universal Security” by Arjen Lenstra shows how much energy needs to be spent on “hacking” a symmetric cryptosystem with keys of different lengths. It turned out that to crack the 228-bit key to the algorithm based on elliptic curves, you need as much energy as is enough to heat all the water on the Earth to the boiling point. However, this statement is correct only if we consider well-known algorithms and use modern equipment, since, strictly speaking, more efficient algorithms or equipment are possible, but their existence is not yet known. The 228-bit key to the EC algorithm for hacking complexity is comparable to the 2380-bit key in RSA, but more on that later. In this comparison, RSA and EC keys are used in an asymmetric cryptosystem, they can be considered equivalent to a 128-bit key in a symmetric scheme.
It is easy to imagine that something “difficult to calculate” will require a large amount of time and energy to calculate. We tend to think that computers can “count anything,” but it turns out that this is far from the truth.
Firstly, there are examples of unsolvable problems, such as the stop problem. However, in the field of cryptography such tasks are not used.
Secondly, if we consider the runtime required by a particular algorithm, then it can be arbitrarily large. This is exactly what cryptography uses. A task is considered computationally “simple” if the time required for the corresponding algorithm to work depends on the size of the input data (measured in bits) as a polynomial: for some positive . In the theory of computational complexity, such problems form a complexity class P. If the running time of the algorithm grows faster than a polynomial, for example, exponentially, then such a task is considered computationally “difficult”.
The complexity class P includes tasks for which there is a deterministic algorithm that works in polynomial time. Another complexity class is NP (in which, presumably, “difficult” problems exist), which is a solvability problem - that is, a problem requiring an answer of “yes” or “no”, the correctness of the solution of which can be verified - that is, to provide proof of the correctness of the solution - in polynomial time. See the word "proof" here? This is the place in which we pass to one-sided functions whose inversion problem belongs to the complexity class NP.

Posted by: xkcd
(One-way functions (with secret input))
By definition, a one-way function is a function that is easy to calculate for any input, but difficult to invert, that is, get the original input with only the result. “Easy” and “hard” refer to the theory of computational complexity mentioned above. Interestingly, the existence of one-sided functions (mathematically) has not been proved, since a rigorous proof of their existence would also prove the inequality of the classes P and NP, one of the millennium problems and an urgent open problem, whose solution promises an algorithmic breakthrough. Therefore, it is necessary to keep in mind that almost all modern cryptography is based on unproven hypotheses.
In their original publication, Diffie and Hellman introduce a new generation of one-way functions, calling them "one-way functions with a secret input" - in English trapdoor function. How do they differ from just one-way functions?
Let's look at their original explanation:
In a cryptosystem with a public key, encryption and decryption are performed by various keys - E and D, respectively, such that the calculation of D from E is practically impossible (for example, requiring instructions). The encryption key E can be publicly disclosed without compromising the key D. This allows any user of the system to send a message to any other user, encrypted in such a way that only the expected recipient can decrypt it. <...> The task of authentication, perhaps, is a more serious telecommunication problem for business transactions, compared with the distribution of keys, since it (authentication) lies at the heart of any system working with contracts and billing for payment.Usually, cryptographic characters Alice and Bob are used to explain the principles of cryptosystem operation (they strive for secure communication). Alice and Bob agree to choose large primes and such that . This choice affects the security of the entire circuit. Number called a module should be simple; moreover, the number should also be simple, but must be the primitive root in the group of residues modulo ; Besides, should be large enough - at least 512 bits in binary representation. Further, the Diffie-Hellman protocol can be described in five simple steps:
- Alice picks (large prime) and computes
- Bob picks (also a big prime) and computes
- Alice sends Bob, Bob sends Alice ( and each of them remains a secret)
- Alice calculates
- Bob is calculating
As a result, Alice and Bob get the same result in construction. - a shared secret.
So, a one-way function with a secret input is such a one-way function that can be reversed by having a piece of special information called a “secret input”. It sounds simple, but in practice, finding such a function turned out to be a non-trivial task - the first decent method turned out to be the progenitor of a whole family of algorithms based on a public key named RSA by the names of its creators: Ron Rivesta, Adi Shamira and Leonard Adleman.
RSA
In RSA, the complexity of inverting a function is based on the fact that factorization (factorization of a number) takes much longer than multiplication or, more precisely, it can be argued that no method for factorizing large numbers in polynomial time was found on a classical computer, although it was not It is proved that such an algorithm cannot exist.
In RSA, as in any other cryptographic system with a public key, there are two keys: public and private. The RSA algorithm takes an input message represented by a bit string and applies a mathematical operation to it (raising to a power modulo a large number) in order to obtain a result indistinguishable from random. For decryption, the result is taken and a similar operation is performed to receive the original message. In asymmetric cryptography, encryption is performed with a public key, and decryption with a private key.
How is this possible? Due to the fact that the values used belong to a finite cyclic group (the set of integers with multiplication in modular arithmetic). Computers do not work very well with arbitrarily large numbers, but the property of the cyclic group is “wrap around” - a number greater than the allowed maximum is “wrapped” to the value from the allowed set. This allows us to use keys with a length of "no more than" a certain number of bits. In cryptography based on elliptic curves, cyclic (multiplicative) groups are also used, but are constructed slightly differently, as we will see later.
At a very primitive level, all RSA does is take two large primes, multiplying them to get the so-called module. All other numbers with which operations will be performed should be between zero and the module value. The module itself will become part of the public key - its length determines the length of the key. The second part of the public key is the number chosen between zero and the value of the Euler function (modern RSA implementations use the Carmichael function instead of Euler) from the module, with some additional restrictions. Finally, you can calculate the private key by solving the modular equation. To encrypt the message, we take the number representing the message and simply raise it to the power equal to the value of the public key, and to decrypt it — to receive the original message, raise it to the power equal to the value of the private key. Due to the cyclical nature of the group, we get the same meaning.
Today, RSA has two main problems, one of which is a consequence of the other. As the key length grows, complexity does not grow as fast as we would like. This is because there is a subexponential (but still superpolynomial ) factorization algorithm. Therefore, in order to maintain the necessary level of protection, the length of the RSA key should grow somewhat faster than that of the ECC key. For this reason, the most common RSA key lengths today are quite large: 2048 and 3072 bits.
A little later, we will see on specific figures how the key length affects the final performance of the cryptosystem by comparing the certificates signed by Let's Encrypt RSA and ECDSA.
E lliptic C urve Digital S ignature A lgorithms
In search of more reliable functions with a secret input, in the mid-80s cryptographers came to use a branch of mathematics devoted to elliptic curves.
It would be too difficult to describe all the details of cryptography based on elliptic curves in one text, so we will not do this. Instead, let's look at a one-way function with a secret input, built on the basis of elliptic curves and the discrete logarithm problem.
There are a large number of review materials and more detailed introductions to this area of cryptography. We would especially like to mention the “ECC: a gentle introduction” by Andrea Corbellini, especially if you are interested in the device.
We, in this material, are interested in a much more “simple” explanation.
An elliptic curve is defined by an equation that looks like this: .
The second object is a cyclic subgroup over a finite field. The following parameters are used in the ECC algorithm:
- Prime number , which determines the dimension of the final field;
- Odds and elliptic curve equations;
- Base point generating the already mentioned subgroup;
- Order subgroups;
- Cofactor subgroups.
As a result, the set of parameters for our algorithms is represented by six .
Points of an elliptic curve belong to a finite field where this is a fairly large prime number. So, we have many integers modulo , where operations such as addition, subtraction, multiplication, taking the opposite are possible. Addition and multiplication work in a similar way to how we described this in terms of the modular arithmetic of the RSA (wrap-around) section.
Since the curve is symmetrical about the x axis, for any point we can take and get the point opposite to it. We immediately stipulate that the point corresponds to zero, i.e. will be simple .
The addition of points on a curve is defined so that, knowing the points and , we can draw a line passing through both of these points, as well as a third - , so that and .
Let's take a look at Mark Hughes's illustrated illustration:
Multiplication by a scalar is determined quite obviously: .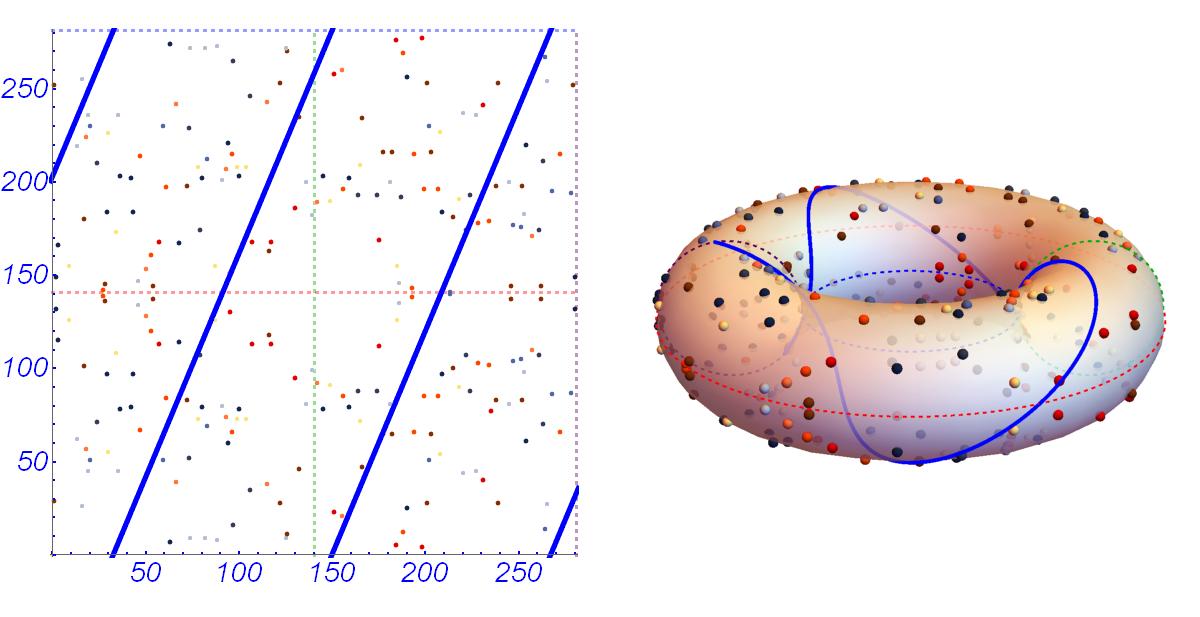
We see a straight line stretched along the surface of the torus. The line intersects two randomly selected points on the curve.
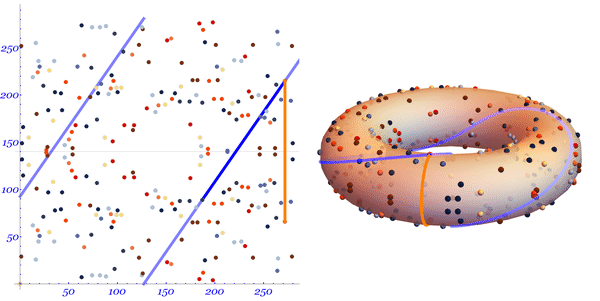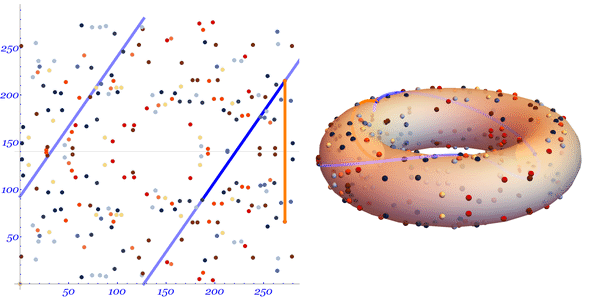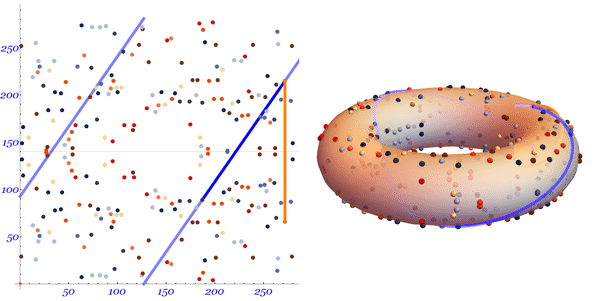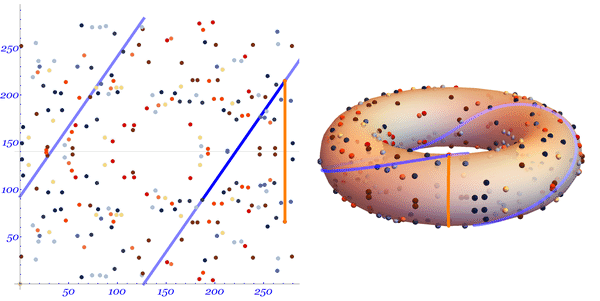
In order to find , we draw a line from the first selected point to the second continuing the line until it crosses the curve at the third point .
After the intersection, reflect the point relative to the abscissa axis in order to find the point .
The one-way function with a secret input in this case is based on the discrete logarithm problem for elliptic curves, and not on factorization, as is the case with RSA. The discrete logarithm problem in this case is formulated as follows: if known and , then how to find such that ?
Both the factorization problem (underlying RSA) and the discrete logarithm for elliptic curves (which are the foundation of ECDSA and ECDH) are considered difficult - in other words, there are no algorithms for solving these problems in polynomial time for a given key length.
Although, usually, I would be bombarded with dirty (at best) rags for mixing key distribution algorithms (ECDH) with signature (ECDSA), I still have to explain how they work together. A modern TLS certificate contains a public key, in our case, from a pair generated using an algorithm based on elliptic curves, usually signed by some authoritative organization. The client verifies the server’s signature and generates a shared secret. This secret is used in a symmetric encryption algorithm, such as AES or ChaCha20. However, the basic principles remain the same: agree on a set (six) of parameters, get a key pair, where the private key is a randomly selected integer (a factor of ), and the public key is a point on the curve. Signature Algorithms Use a Base Point which is a generator of a subgroup of order ( Is a large prime), so where 0 is the neutral element of the group. The signature proves that a secure connection is established with an authenticated party - a server that has a TLS certificate (public key) signed by an authoritative organization for a given server name.
(EC) DH (E) + ECDSA = Modern form of handshake
In modern TLS version 1.3, the client and server generate a key pair on the fly, establishing a connection. This is called the "ephemeral" version of the key exchange algorithm. The most popular TLS libraries support just such a protocol version. For the most part, the Edwards elliptic curve 25519 , proposed by Daniel Bernstein Jr. (djb), which provides a 128-bit level of protection, is used today. Since 2014, this curve has been available for creating key pairs in the openssh library. However, as of the end of 2019, browsers still do not establish a TLS session with servers using the public key to the EdDSA signature algorithm.
Let's look at how everything works in TLS 1.3.
In the latest version of the protocol, key distribution mechanisms are limited to (EC) DH (E) - x25519 is the most common function for obtaining a common key - it is supported by most browser and server TLS libraries. The cipher suite consists of only three entries: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 and TLS_CHACHA20_POLY1305_SHA256. For those of you who are familiar with how the cipher suites were named in the previous version of the protocol - TLS 1.2, it is obvious that the indication of the key exchange mechanism was "separated" from the cipher suite during the transition to TLS 1.3. Also, static RSA and DH key exchange methods were thrown out of the specification. Even session recovery in TLS 1.3 with the help of PSK and tickets of the previous session occurs according to the ECDHE protocol, where the last E - ephemerality is especially important. Also, in TLS 1.3, it is not possible to set your own values for the Diffie-Hellman mechanism - only a predefined set is left in the protocol specifications, there is a consensus regarding the security of this set.
Of particular interest is the fact that modern asymmetric encryption mechanisms work differently. In ECC (in particular, when using ECDSA certificates) we use keys of relatively short length compared to RSA in order to get to acceptable levels of security. This allows you to use strong asymmetric cryptography and key exchange schemes even on devices that, it would seem, should not have enough power for the necessary operations - for example, smart cards.
Firstly, it is necessary to clarify what the term “hybrid cryptosystem” means as it applies to the description of TLS 1.3. The hybrid cryptosystem uses an asymmetric (with a public key) encryption scheme to establish a shared secret, which is then used as a key in a symmetric block or stream encryption algorithm.
Secondly, there is a public key infrastructure (PKI) and certificate (CA) infrastructure. It is interesting that in 2004 Martin Hellman mentioned one of the “unsung heroes” - Loren Könfelder, whose thesis on defense of the MIT bachelor’s diploma was the possibility of creating a tree structure - what we know today as PKI. But let's get back to the certificates.
The fact that the server really owns the private key is verified by its signature, which can be verified using the public key. And the certificate file on the server certifies that a specific public key belongs to a specific server. This means that you are establishing a secure connection with the desired interlocutor, and not an impostor - your bank, not a cyber fraud.
TLS 1.3 has significantly improved the negotiation scheme compared to previous versions of the protocol. Now the server signs all the information received in the handshake at the time of creating such a signature: client hello and its own server hello, along with a set of ciphers selected for use. Let's take a look at the corresponding interaction description section from RFC 8446 :
Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data]
In TLS 1.3, the client sends its part of the key (along with the necessary parameters) and the list of signatures available in the first message (Client Hello). The keys necessary at this stage are created by the client on the fly - the user does not even notice this. Next, the client and server exchange this information to create a common secret - a session key that is created (or, more precisely, is derived) from the pre-master pair received after the server answered the client with its message (Server Hello).
On the “Server Hello” side, you can see the record corresponding to the transfer of the certificate to the client (Certificate *), along with the CertificateVerify * check, which confirms that the party really has a private key related to the corresponding public key record, then creating a session (symmetric) key pair in case of success. In other words, the party requesting the data (client) has successfully verified the authenticity of the responding party (server) by switching to using a shared secret.
The two main cryptographic operations are protected in this transfer - the creation of a signature and verification of a signature. These operations are usually performed at different ends of the connection, as most often clients verify the authenticity of the server. The signature is essentially a confirmation of the ownership of the private key corresponding to the public key. That is, that we receive data from the signatory, and make sure that the message was not changed during the transfer.
When using the RSA algorithm, as we will demonstrate a little later on the numbers, the operation of creating a signature is the most expensive. Since we sign with a 2048 or 3072-bit key, such an operation significantly loads the server - much stronger than the client during its (signature) verification.
In ECDSA, we operate with relatively short keys (in the benchmark example, we will look at ECDSA using the NIST P-256 curve (or secp256v1), but these keys are involved in more complex operations. As a result, using ECC can be represented as an “inverted” RSA with performance points of view: the client is much heavier than the signature verification operation, while the server easily handles the signature creation operation, which is confirmed by the measurements we provide in the benchmark section.
This effect helps to scale the Internet - since modern clients are almost as powerful as servers (if we consider only the clock speed of the processor core), they can effectively take on a computationally difficult operation without problems. The server, in turn, can use the freed up computing power to create more signatures and, as a result, establish more sessions.
Certificate Signature at Let's Encrypt
We will provide our reader with a simple and understandable instruction on which you can independently create a server capable of establishing a TLS session using an ECDSA key pair in which Let's Encrypt is publicly signed and is included in the certificate of trust chain as a certificate.
We decided to show the full path from creating keys, creating a certificate signing request (CSR) for Let's Encrypt and transferring it to a signature using the certbot utility, which returns the necessary chains and the ECDSA certificate itself.
First you need to create a key pair. For this we will use the OpenSSL library. The OpenSSL User Guide says that creating keys to algorithms based on elliptic curves occurs using a special command dedicated to the family of algorithms based on elliptic curves.
openssl ecparam -genkey -name -secp256v1 -out privatekey.pem
To verify that our team worked correctly, we execute the ec command indicating the path to the newly created file containing the private key.
openssl ec -in privatekey.pem -noout -text
The output should show us the curve used, with which the key was generated.
The next step is quite important when creating a CSR - in order to not fill out the questionnaire necessary for signing a certificate each time, we need a configuration file. Fortunately, almost all of the work for us was done by Mozilla, creating the “ SSL Configuration Generator ”. In it, you can choose from a variety of options for server modes with which you can establish a TLS connection. The clean OpenSSL config, for some reason missing from the Mozilla generator, looks like this:
[ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com
Note: you do not have to have a configuration file - if it is not there, you will be asked to fill in all the fields on the command line. With the configuration file, the path to which we specify in the next command, the process is simplified.
The next step is to create the certificate signing request (CSR) itself. For this, we have a convenient OpenSSL team.
openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem
We can also verify the correctness of the newly created CSR.
openssl req -in csr.pem -noout -text -verify
Finally, we come to the final stage - using the ACME client, certbot, we will transfer our request for signing the Let's Encrypt organization certificate.
Certbot will not only help you get a certificate, but it also has many other great options. We add that if you are new to cryptography with a public key and do not really understand the public key infrastructure that exists at the moment, it is better to use the
--dry-run
option before trying to get a real certificate for any of your domains.
certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem
In this case, the certbot client verifies that the list of required domains requested on the command line matches the list in the certificate signing request (CSR). Inside the
--dns-somednsprovider
we
--dns-somednsprovider
bit, as there are many ways to confirm Let's Encrypt that you own a certain portion of Internet traffic. But if you use some kind of cloud provider, such as DigitalOcean, AWS, Azure, Hetzner, whatever - perhaps for you there is already an easier way to provide the information required for certification, because your provider has taken care of the integration tool.
After that, if you are sure that the parameters passed to the CSR using the certbot to Let's Encrypt are correct, just remove the
--dry-run
parameter from the command and continue.
If successful, the client will return several certificates to you: the signed certificate itself, the intermediate and root certificates, as well as a combination of the latter in the form of a chain of certificates, all in .pem format.
OpenSSL has a command that we use in order to look inside the certificate:
openssl x509 -in chainfilepath.pem -noout -text
It should now be clear that Let's Encrypt signed the certificate using the SHA256 hash algorithm. In addition to this, Let's Encrypt is only planning to add root and intermediate signatures to ECDSA, so for now it remains to be content with intermediate RSA signatures. But this is not scary, as you will use the ECDSA public key anyway.
At the end of this section, we would like to add some information about comparing the key lengths of various algorithms. In information security, it is customary to say that the security level is 2 ^ x, where x is the bit length (RSA is some exception, since it grows somewhat slower than the exponent). To approximate how the keys of various algorithms are compared with each other, we refer to the OpenSSL wiki page:
| Symmetric key length
| RSA Key Length
| Elliptic Curve Key Length
|
| 80
| 1024
| 160
|
| 112
| 2048
| 224
|
| 128
| 3072
| 256
|
| 192
| 7680
| 384
|
| 256
| 15360
| 512
|
As you can see, the differences are noticeable. Although for now, Let's Encrypt allows you to receive signed certificates only on the keys of only two elliptical curves - 256 (secp256v1) and 384 (secp384r1).
Known difficulties as well as the NSA

Posted by: xkcd
Perhaps the central problem in using cryptography based on elliptic curves was the need for a very neatly implemented random number generator, which is required to create keys of a certain security level.
A huge scandal was associated with the Dual_EC_DRBG algorithm - it took many years to resolve it. There is uncertainty about the patent base around ECC - it is known that many patents belonged to Certicom, which was acquired by Blackberry. There are also several known Blackberry ECC certification cases. Finally, there is a certain mistrust of the NIST standards, which could be influenced by the NSA or any other US intelligence agency.
Errors in the implementation of cryptographic standards is a completely orthogonal topic. In 2010, the PlayStation 3 suffered as a result of the leak of Sony's private key due to incorrect implementation of the ECDSA algorithm - Sony could not cope with the RNG and supplied the same random number, which made it possible to solve the function with a secret input. OpenSSL suffered the following year, however, it quickly fixed a vulnerability that allowed it to obtain a private key using a time attack - more details can be found in the original research publication .
At a RSA conference in 2013, a group of researchers presented a research paper entitled “ Randomly Failed! ”Dedicated to SecureRandom Java class vulnerabilities. Six months later, things started with Bitcoin wallets created using a cryptographically unsafe pseudo random number generator.
Due to the fact that several serious vulnerabilities were discovered in a short period of time, in the same August 2013, the IETF released RFC 6979 , which describes the deterministic generation of k when creating a key. We could write that the problem was solved in this way, but we won’t - at any time, researchers may find new errors in the implementation due to unnecessary deviations from the protocol specifications.
And a few words about the NSA. If you have not been aware of the history of Dual_EC_DRBG - take some time and read the relevant materials, you will not regret that you figured out the details. Edward Snowden became a part of this story, because it was because of his leaks in 2013 that all doubts that existed were confirmed. This resulted in the fact that many eminent cryptographers lost confidence in NIST, since it was this organization that created and described many of the elliptic curves and algorithms that work in ECDSA.
Curve 25519 authored by Daniel Burnshite and the Diffie-Hellman function for key distribution is the answer to many of the above questions. And, as we already wrote, there is a steady movement towards EdDSA. In the case of the NIST curves, no confirmation of their vulnerability has yet been found, and as for the experience with random numbers, it was quite painful and contributed to the rapid assimilation.
To conclude this part, we would like to quote John von Neumann: "Anyone who has a weakness for arithmetic methods for obtaining random numbers is sinless beyond any doubt."
Some benchmarks
We used the NGINX 1.16.0 server with the OpenSSL library version 1.1.1d to conduct tests with two certificates. As already mentioned, at the moment Let's Encrypt allows you to use only the prime256v1 and secp384r1 algorithms to create a certificate signing request, as well as not providing root and intermediate certificates with an ECDSA signature, you are probably dealing with this feature while you read this note.
| Signature type | Handshakes per minute | Handshakes per second |
| ECDSA (prime256v1 / nistp256) | 201516 | 3358.600 |
| RSA 2048 | 58354 | 972.567 |
As you can see, on the same core of the Intel® Xeon® Silver 4114 CPU @ 2.20GHz (released in the third quarter of 17), the total difference between ECDSA performance and the generally accepted RSA with a key length of 2048 bits is 3.5 times.
Let's look at the results of running the openssl -speed command for ECDSA and RSA on the same processor.
| Signature type
| sign
| verify
| sign / sec
| verify / sec
|
| RSA 2048 bit
| 0.000717s
| 0.000020s
| 1393.9
| 49458.2
|
| 256 bit ECDSA (nistp256)
| 0.0000s
| 0.0001s
| 38971.6
| 12227.1
|
Here we can find confirmation of the previously written thesis on how the computational operations of the signature and its verification for ECC and RSA differ. Currently, armed with TLS 1.3, cryptography based on elliptic curves gives a significant increase in server performance with a higher level of protection compared to RSA. This is the main reason why we at Qrator Labs recommend and strongly encourage customers who are ready to use ECDSA certificates as well. On modern CPUs, the performance gain in favor of ECDSA is 5x.
If you are interested in how your (home or server) processor handles cryptographic computing, run the openssl speed command. The
-rsa
,
-ecdsa
and
-eddsa
allow you to specify the algorithms of interest for benchmarking.
The future (in superposition)
Ironically enough, in the process of writing this material, Google announced "achieving quantum superiority . " Does this mean that we are already in danger and all the progress made to the current moment is no longer able to ensure secrecy?
Nope.
As Bruce Schneier wrote in the essay “Cryptography after Alien Landing” for the IEEE Security and Privacy Circular, a quantum computer can really deliver a serious blow only to asymmetric cryptography with a public key. Symmetric algorithms will remain persistent.
But to continue, we will give the floor to Mr. Schneier himself:
There is another future scenario that does not require a quantum computer. While we now have several mathematical theories that underlie the one-sidedness used in cryptography, proof of the validity of these theories is actually one of the biggest open problems in computer science. Just as a smart cryptographer can find a new trick that facilitates hacking a particular algorithm, we can imagine aliens with enough mathematical theory to crack all encryption algorithms. Today it seems ridiculous. Public key cryptography is a number theory and is potentially vulnerable to mathematics-minded aliens. Symmetric cryptography is so non-linear, so simple to create and complicate, and also how easy it is to lengthen keys, what a future is unimaginable. An example is the AES variant with a 512-bit block and a key size, as well as 128 rounds. If mathematics is not fundamentally different from our current understanding, then such an algorithm will be safe until computers are made of something other than matter and occupy something other than space.
But if the unimaginable happens, it will leave us only with cryptography based solely on the theory of information: disposable cipher-notepads and their variants.
Bruce Schneier perfectly describes the area where, in addition to implementation errors, the main vulnerabilities of modern cryptography can be found. If somewhere there is a group of well-off mathematicians, cryptanalysts and cryptographers, together with computer engineers working on the proof or refutation of some especially complex mathematical problems (such as P? = NP), who have managed to achieve some progress in this activity at the moment - our position is vulnerable. Having rejected conspiracy theories, one can say that such progress in the fields of computer science, information theory, and computability theory can hardly be hidden. Such an event would have entered the names of their own creators on the pages of History and, in particular, in the textbooks of Internet History, which is invaluable to any so intelligent individual or group. So a similar scenario may be discarded as impossible.
It is also unclear whether such successes in quantum computing will be made in the next 5 years - and after all, there are already cryptographic primitives suitable for use in the post-quantum world: lattices, using supersingular isogenization of elliptic curves, hash functions, error correction codes. Now, security experts are only experimenting with them, but there is no doubt that, if necessary, humanity will find a way to quickly use new algorithms on any scale.
It remains only to add that for the next decade, cryptography based on elliptic curves seems to be ideally suited to the goals and needs that most of its users set for themselves, providing security and high performance.