The mathematical justification of the inappropriateness of running down the escalator in the subway

Contrary to the rules of using the subway, in order to save time, each of us ran at least once in our lives down the escalator. At first glance, it seems that this is absolutely logical and correct: if you want to leave faster - try to be on the platform as early as possible. However, almost immediately the following scenario comes to mind: you headlong down the escalator, go down to the platform, and the car doors close right in front of your nose. While you are waiting for the next train - people who got up on the escalator at the same time as you have time to stand still quietly go down and take the next train. In this case, there is no gain. So how rational is it to run down the escalator and is it worth doing it at all? I hasten to please you - the answer is found! Below is a mathematical justification for the inexpediency (yes, it is NOT) to run down the escalator in the subway.

Task statement

Before turning to mathematical reasoning, it is worth mentioning that, of course, I am not the first to think about this issue at all. On the Internet you can find a sufficient number of articles and even news stories of federal channels on this topic. However, each time the essence of this kind of experiment consists in the usual run down the escalator with the subsequent comparison of the time gained with the time of the person standing on the escalator. Slightly better if the authors are trying to assess the effectiveness of downhill. Even better if they still provide statistics. For statistics, by the way, I’ll say a special thank you a little lower. In connection with the lack of clarity of these experiments and the lack of practical conclusions, I was conceived, and subsequently carried out, an analysis of the ongoing process.



And so, we formulate the conditions of the problem and denote the restrictions:

1. The experiment (mental) involves two people who approach the escalator at the same time at a random moment in time and have no idea where the train is.
2. One of these people is standing on an escalator and spending time on a descent. $$ equal to the time of movement of the escalator.
3. The second accelerates down the escalator, increasing its speed in $$ times, thereby reducing the descent time by the same number of times: $$ .
4. Effective is considered such an accelerated descent, which led to the fact that the person standing on the escalator does not have time to board the train, in which the person running on the escalator has time to board.
5. Denote by $$ - the probability of an effective descent. Then, according to the Nash equilibrium, a person is ready to take a chance and run down the escalator only if the probability of an effective descent is greater than or equal to the probability of an ineffective descent or stop in place, i.e. 0.5. If the probability of an effective descent is greater than or equal to 0.5, the decision to run down the escalator will be called appropriate . If less than 0.5 - impractical .
6. We neglect the fact that in real life, as a rule, it is necessary to go some further distance to the car after leaving the escalator or to wait for people to leave the car, trains go at variable intervals and stand motionless for a while before opening and after closing the doors, that is, we will assume that if at the moment of leaving the escalator the train is at the station, then its doors are open and the experiment participant instantly ends up in the car, the train itself opens (closes) the doors and arrives (leaves) to the station (from the station) instantly and dnomomentno.

Decision progress

Let's draw the time axis (Fig. 1). The entire axis will be consecutive intervals between trains. Hereinafter, only one interval will be considered. Divide the interval shown into 4 equal segments. Point 0 on this axis corresponds to the moment the train leaves the station. Point 3 corresponds to the arrival of the train and the opening of the doors. Point 4 - closing the doors and departure of the train. Thus, for the convenience of graphical representation and calculations, the interval between trains is counted between the moments of departure of trains from the station. The first 3 segments are the time passengers are forced to wait for the arriving train. The fourth segment is the train’s stopping time, when passengers can board it. Put also that time $$ (time of descent on the escalator) is equal to two segments. Coefficient $$ It is equal to 2, that is, the run time is 2 times less and equal to one segment.







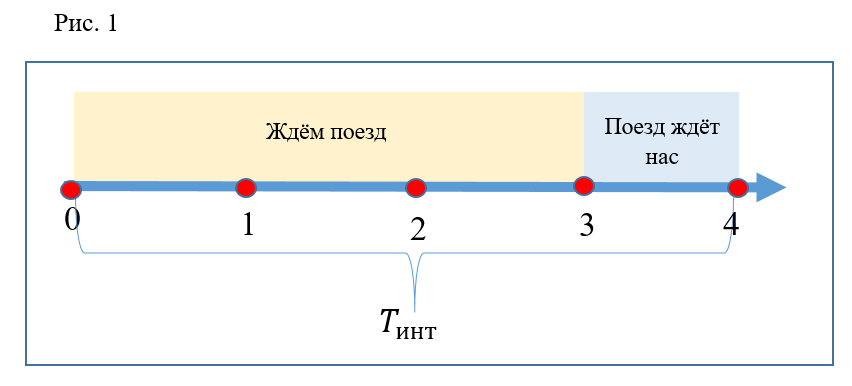
Now, to determine the probability $$ , find out in what period of time the decision to go jogging will lead to the fact that the descent will be effective. For example, if our participants approach the escalator at time 0, then the first will be on the platform at time $$ (Fig. 2), and the second earlier, at the moment $$ . But, as can be seen from the figure, at none of these moments of time there is a train at the station, which means that running down was inefficient.







Consider another case (Fig. 3): the participants in the experiment approach the escalator at time 2. As in the previous case, the first will be on the platform at time $$ , and the second earlier, at the moment $$ . But it is obvious that at both times the train is at the station. So, both will have time to board the same train, therefore, running down was just as inefficient.







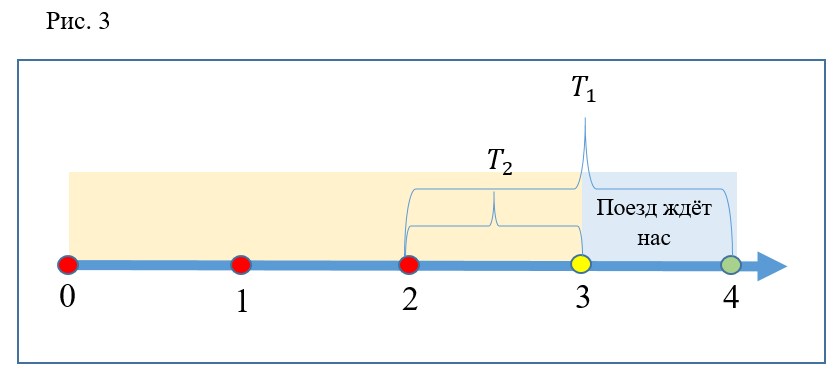
Further, it is easy to understand that at any time in the interval from 2 to 3, running downhill is effective, since the escaped person always manages to board the train, and not the escaped one. If you choose time points between 3 and 4, then both participants are late for the train and are forced to wait for the next one together, that is, running again is ineffective.



It turns out that out of 4 conventional time periods, it is effective to run down only if the participants approach the escalator between 2 and 3 times (Fig. 4). The probability of getting into it is 1/4. Consequently, under the given conditions of the task, the decision to run down is impractical, since the second participant is more likely (with a probability of 3/4) to run in vain and will be forced to wait for the train along with the first, who came down later.







The following remarks will be completely fair:

1. Intervals between trains can both decrease and increase. The parking time may increase, and the waiting time may decrease (with the same interval) and vice versa.
2. The speed of the escalator down is constant, but the descent time can vary, since the stations can be more or less deep.
3. The second participant may well run not 2, but 3 or even 4 times faster than the escalator.

To assess the impact of changes in the above factors, it is necessary to derive the relationship between these values ​​and the probability of getting on the escalator at a time when it is effective to run down.



To do this, we will depict another case (Fig. 5). Leave all the original data unchanged with the exception of one: coefficient $$ increase to 4. That is, the second participant will be at the bottom 4 times faster than the first. For the convenience of the image, we divide our interval into 8 equal parts. Thus, the descent time on the escalator is now equal to 4 segments, the train stops at two, the waiting time is 6, and the descent time to run alone. It is not difficult to find out that now the length of the “effective” time interval (from 4 to 7 points in time) is 3. That is, the probability $$ equal to 3/8. This is already more than in the first case, but we did not carry out these changes at all to assess the probability.







Based on Figure 4 and Figure 5, it is obvious that the length of the “effective” segment is $$ . Divide it by the length of the interval and get the probability $$ where $$ .

We perform a series of transformations: $$$$ .

The final formula: $$ .



Based on this formula, several fundamental conclusions can be drawn at once:

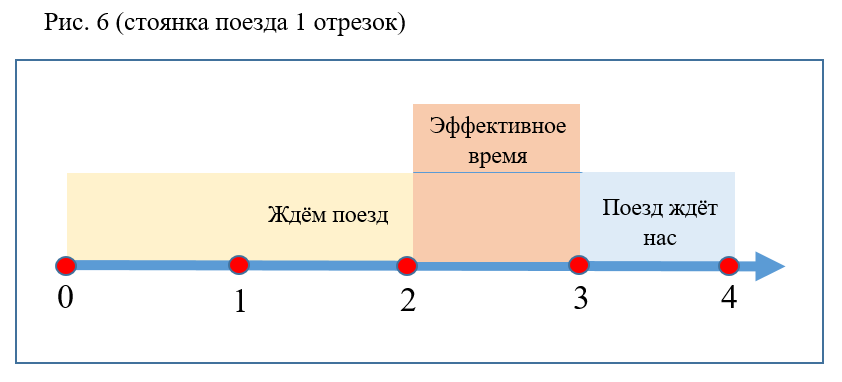
1. The probability value is not affected by changes in the stopping time and train waiting unless the total interval is changed (Fig. 6).
   
   
   
   
   
   
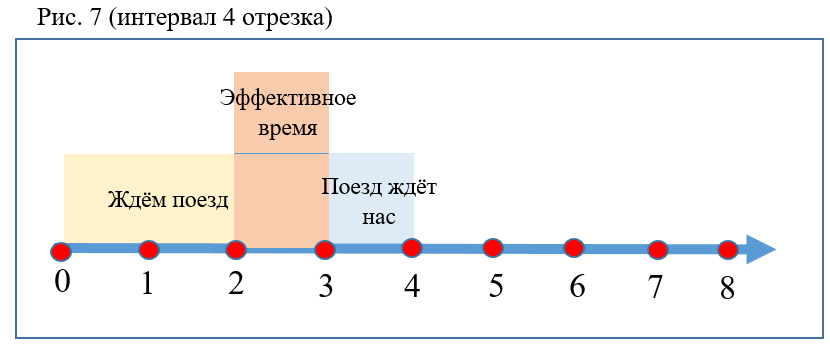
2. The larger the interval between trains, the lower the probability P (Fig. 7).
   
   
   
   
   
   
3. The probability increases if the ratio of the descent time on the escalator to the interval and / or the coefficient K increases.
   
   

Fidelity check

Now let's see how true the derived formula is?



To verify the correctness of the formula, we turn to the statistics, which were very handy back in 2014 by The Village correspondent. I express my recognition and, naturally, at the end of the article I will leave a link to the original article. It’s also good that the statistics are presented as visual infographics.



Experiment 1. Metro station Chekhovskaya







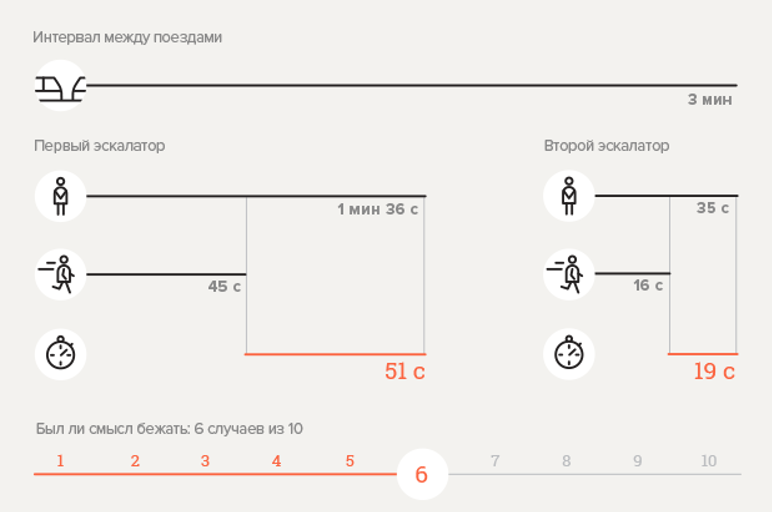
Calculate the probability $$ .

Here $$ ; $$ ; $$ ; $$ ; $$ .



The result obtained, as can be seen, diverges from the experimental data. Is the formula wrong? Not! It can be seen from the infographic that the descent to the station involves a trip on two escalators, however, the transition time between them is not taken into account. If, for reliability, we assume that the transition takes at least 30 seconds, then, substituting a new value $$ we get: $$ ; $$ , which is much closer to the experimental result. It is also worth noting that the experiment provided for only 10 repetitions. By increasing the number of repetitions, it is possible to achieve almost complete coincidence of the calculated data with the results obtained during the experiment.



Experiment 2. Metro station "Victory Park"







Calculate the probability $$ .

Here $$ ; $$ ; $$ ; $$ ; $$ .

It can be seen that we got a probability greater than one. But there is no contradiction here. If you look at the general form of the formula, it becomes obvious that in the case when the descent time on the escalator is equal to the interval between trains, then an increase in speed by at least 2 times will make the probability that accelerated descent is effective equal to 0.5. If the travel time of the escalator is greater than the interval, then with the same coefficient $$ the probability of catching a train earlier will only increase. Finally, if the descent time on the escalator is 2 or more times the interval, the running person in 100% of cases will be in time for the train that the remaining on the escalator will not be in time. It is this effect that we observe in this experiment: the correspondent concluded that he washed away in 10 out of 10 cases.



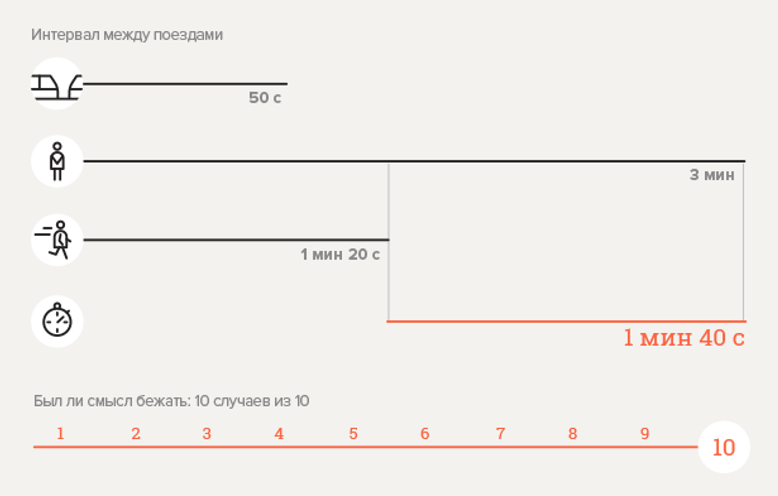
Experiment 3. Park Kultury metro station







Calculate the probability $$ .

Here $$ ; $$ ; $$ ; $$ ; $$ .



Error again? Not at all. It can be seen that, as stated above, the descent time on the escalator is 2 times the interval between trains. Running time is 2 times less. It turns out that every descent should be effective. But do not forget that before starting the discussion we made the assumption regarding the instantaneous closing of doors and at least the instantaneous departure of the train from the station. If you imagine such an option as in Figure 8, it becomes clear that in real life a runaway person may not have time to sit down at point 1 (for example, the train will leave a little earlier) and at point 2 the train, on the contrary, will delay a bit, and then the non-running person will sit in it with the late-running person who was late for the previous train.







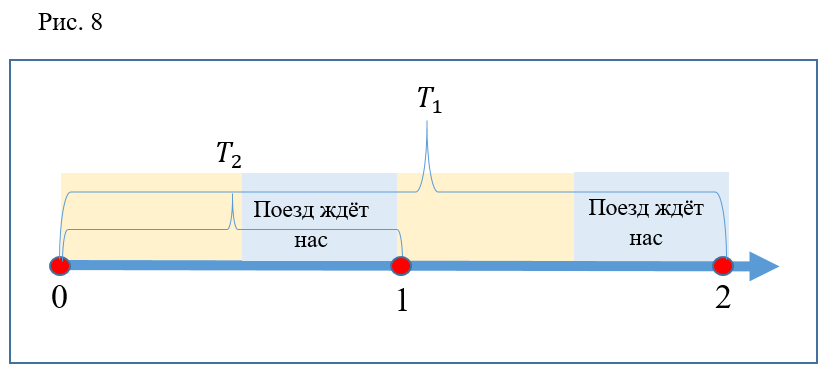
I suppose that in both "ineffective" times it happened. There is every reason to argue that with an increase in the number of repetitions of the experiment, the percentage of "effective" runs will tend to 100%.

conclusions

Now that, based on the available experimental data, it was possible to confirm the correctness of the formula, we will analyze it and draw conclusions. Since at the very beginning we agreed that we would consider the decision to run downward expedient if the probability of an effective descent is greater than or equal to 0.5. That is, literally, if we can be sure that at least in half the cases we will run for good reason, then it is really worth taking the risk and running, because if we are late, we will practically lose nothing. Based on the foregoing, we rewrite the probability formula as follows: $$ .



It is interesting that, as we have already found out, it makes sense to always run when $$ . At the same time, it is also true that if $$ , no matter how fast you run, the probability of getting on a train earlier is less than 0.5, since it is obvious that $$ will never be greater than or equal to 1.



Now let's take a look at the speed of the correspondent. On average, it is about 2 times the speed of the escalator (descent time is 2 times less). In general, these data coincide with the results of my own experiments (I don’t see the point of bringing them). As a rule, developing speed for which the K coefficient would be at least 3 is already difficult: on a real escalator there are many who want to run down and, moreover, people standing on their left or their things (bags, suitcases) may interfere. Means $$ , but $$ . That is, a decision to accelerate will be appropriate only if the ratio $$ not less than 1. And this is possible only when the time of descent on the escalator down is not less than the interval between trains. In a real metro, where the average interval between trains is 2 minutes, not all stations can boast a long descent. As a rule, even in the St. Petersburg metro, the escalator travel time is about 1 minute 30 seconds, that is, 0.75 times less than the interval. From this follows the very obvious and most important fundamental conclusion: if you know for sure that the escalator at this station moves less than the interval between trains, then it is not practical to run along it.



PS Please take into account the fact that this task does not take into account the need to get into a specific carriage. It is only about getting on the platform and then boarding the train.



Experimental data source: The Village . Thanks again!