Partly due to the popularity of Minecraft , there has recently been a growing interest in the idea of ​​the game, which takes place in a cubed world built of 3D relief and filled with elements such as caves, cliffs and so on. Such a world is an ideal application for noise generated in the style of my ANL library. This article arose from discussions of my previous attempts to implement this technique. Since then, minor changes have appeared in the structure of the library.



In previous posts, I talked about using 3D noise features to implement Minecraft-style terrain. After that, the library evolved a bit, so I decided to return to this topic. Since I had to answer many questions about this system, I will try to talk more about the concepts involved. To make the basic concepts clearer, I will start with the idea of ​​generating a 2D terrain used in games like Terraria and King Arthur's Gold, and then expand the system to 3D examples like Minecraft. This will allow me to demonstrate concepts more effectively using images as an example.



This system was developed taking into account the following abstract goal: we should be able to pass the coordinate of a certain point or cell to the system and determine what type of block should be in this location. We want the system to be a “black box”: we pass it a point, return the block type. Of course, this applies only to the initial generation of the world. Blocks in such games can be changed by the player’s actions, and it will be inconvenient to try to describe such changes using the same system. Such changes must be tracked in some other way. This system generates the original world, pristine and untouched by the hands of the player and other characters.



Perhaps this technique is not suitable for modeling systems such as grass or other biological entities, given that such systems themselves are complex entities that are not so easy to model implicitly. The same applies to systems such as falling snow, ice formation, etc. ... The technique described in the article is an implicit method , i.e. one that can be estimated at a point, and whose value at a given point does not depend on the surrounding values. Biological and other types of systems in order to perform accurate simulations usually need to consider environmental values. For example: how much sunlight falls on a block? Is there any water nearby? These and other questions need to be answered to simulate the growth and spread of biological systems, as well as, to a lesser extent, other types of climate-related systems. Also, this technique is not suitable for modeling water. In this system there is no concept of flow, knowledge of fluid mechanics or gravity. Water is a complex topic, requiring many complex calculations.



So, we are just modeling the earth and stones. We need a function that tells you what the given location should be: earth, sand, air, gold, iron, coal, etc. ... But we will start with the simplest. We need a function that says whether the block is solid or hollow (filled with air). This function should simulate the earth surrounding us. That is, the sky is above, the earth is below. So, let's take on the biblical task, and separate the sky from the earth. To do this, we study the Gradient function. The Gradient function is passed a line segment in an N-dimensional space (i.e., in any coordinate space, whether 2D, 3D, or higher), and it calculates the gradient field along this segment. Incoming coordinates are projected onto this segment and their gradient value is calculated depending on where they lie relative to the end points of the segment. Projected points are assigned values ​​in the interval (-1.1). And this will be a good start for us. We can define the Gradient function along the Y axis. At the top of the interval, we compare the gradient field with -1 (air), and at the bottom with 1 (earth).

 terraintree =
 {
	 {name = "ground_gradient", type = "gradient", x1 = 0, x2 = 0, y1 = 0, y2 = 1}
 } 

(I’ll explain the record briefly. The code for the examples is written in the Lua declaration table. For more information about the format, see the section on Lua integration . In essence, the format is designed for parsing by a special class that reads ads and turns them into noise module instance trees. I prefer this the format is more verbose step-by-step C ++ format, because it is more compact and cleaner. In my opinion, the source code is more readable and compressed than C ++ code. For the most part, the declarations are easy to read and understand. Modules have names, sources are specified name or value. Lua code used to parse table declarations is included in the source code in case you want to use these declarations directly.)



In the case of 2D, the Gradient function receives a straight line segment in the form (x1, x2, y1, y2), and in the case of 3D, the format is expanded to (x1, x2, y1, y2, z1, z2). The point formed by (x1, y1) denotes the beginning of the line segment mapped to 0. The point formed (x2, y2) is the end of the segment mapped to 1. That is, here we map the line segment (0,1) -> ( 0,0) with a gradient. Therefore, the gradient will be between the regions of the function Y = 1 and Y = 0. That is, this strip forms the dimensions of the world in Y. Any part of the world will be in this strip. We can snap any region along X (almost ad infinitum, but here double



precision limits us), but everything is interesting, i.e. the surface of the earth will be within this band. This behavior can be changed, but within it we have a greater degree of flexibility. Just do not forget that any values ​​that are above or below this band are most likely to be uninteresting, because the values ​​above are most likely to be air, and the values ​​below are ground. (As you will soon see, this statement may well turn out to be erroneous.) For most of the images in this series, I will match the square region given by the square (0,1) -> (1,0) in 2D space. Therefore, at the beginning our world looks like this:









Nothing interesting so far; Moreover, this image does not answer the question “is the given point solid or hollow?”. To answer this question, we need to apply the Step Function (piecewise defined function). Instead of a smooth gradient, we need a clear separation, in which all locations on one side are hollow, and all locations on the other side are solid. In ANL, this can be implemented using the Select function. The Select function receives two incoming functions or values ​​(in this case they will be equal to “solid” and “hollow” (Open)), and selects them based on the value of the control function (in this case, Gradient). The Select module has two additional parameters, threshold and falloff , which affect this process. At this stage, falloff is undesirable, so we will make it equal to 0. The threshold parameter decides where the dividing line between Solid and Open will go. Everything that will be greater than this value in the Gradient function will turn into Solid, and everything that is less than the threshold will become Open. Since Gradient compares the interval with values ​​from 0 and 1, it would be logical to place the threshold at 0.5. So we divide the space exactly in half. Value 1 will be a solid location, and value 0 will be hollow. That is, we define the function of the earth plane as follows:

 terraintree =
 {
	 {name = "ground_gradient", type = "gradient", x1 = 0, x2 = 0, y1 = 0, y2 = 1},
	 {name = "ground_select", type = "select", low = 0, high = 1, threshold = 0.5, control = "ground_gradient"}
 }

Comparing the same area of ​​the function as before, we get something similar:









This picture clearly answers the question whether the given point is solid or hollow. We can call the function with any possible coordinate of the 2D space, and its result will be either 1 or 0, depending on where the point is located relative to the surface of the earth. However, such a function is not particularly interesting, it is just a flat line stretching to infinity. To revive the picture, we use a technique called “turbulence”.



“Turbulence” is a complex designation of the concept of adding values ​​to the incoming coordinates of a function. Imagine that we call the above function of the earth with the coordinate (0,1). It lies above the ground plane, because at Y = 1 the gradient has a value of 0, which is less than threshold = 0.5. That is, this point will be calculated as Open. But what if, before calling the function of the earth, we somehow transform this point? Suppose we subtract a random value from the Y coordinate, for example, 3. We subtract 3 and get the coordinate (0, -2). If we now call the ground function for this point, then the point will be considered solid, because Y = -2 lies below the Gradient segment corresponding to 1. Suddenly, the hollow point (0,1) turns into a solid. We get a block of solid stone hanging in the air. This can be done with any point in the function by adding or subtracting a random number from the Y coordinate of the incoming point before calling the ground_select function. Here is an image of the ground_select function showing this. Before calling the ground_select function, a value in the interval (-0.25, 0.25) is added to the Y coordinate of each point.









This is more interesting than a flat line, but not very similar to the earth, because each point moves to a completely random value, which creates a chaotic pattern. However, if we use a continuous random function, for example, Fractal from the ANL library, then instead of a random pattern we get something more controllable. Therefore, let's connect a fractal to the earth plane and see what happens.

 terraintree =
 {
	 {name = "ground_gradient", type = "gradient", x1 = 0, x2 = 0, y1 = 0, y2 = 1},
	 {name = "ground_shape_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 6, frequency = 2},
	 {name = "ground_scale", type = "scaleoffset", scale = 0.5, offset = 0, source = "ground_shape_fractal"},
	 {name = "ground_perturb", type = "translatedomain", source = "ground_gradient", ty = "ground_scale"},
	
	 {name = "ground_select", type = "select", low = 0, high = 1, threshold = 0.5, control = "ground_perturb"}
 }

Here it is worth noting a couple of aspects. First, we define the Fractal module, and chain it to the ScaleOffset module. The ScaleOffset module scales the output fractal values ​​to a more convenient level. Part of the terrain may be mountainous and require a larger scale, and another part - more flat and with a smaller scale. We will talk about different types of terrain later, but for now we will use them for demonstration. The output values ​​of the function will now give the following picture:









This is more interesting than just random noise, right? At least, it looks more like land, although part of the landscape looks unusual, and the flying islands are completely strange. The reason for this was that each individual point of the output map is randomly shifted by a different value determined by the fractal. To illustrate this, we show the fractal output that performs the distortion:









In the image above, all black dots have a value of -0.25, and all white dots have a value of 0.25. That is, where the fractal is black, the corresponding point of the earth's function will be shifted "down" by 0.25. (0.25 means 1/4 of the screen.) Since one point can be shifted slightly, and the other point above it in space can be shifted more, there is a possibility of protrusions of rocks and flying islands. The protrusions in nature are quite natural, unlike the flying islands. (Unless we are in the movie “Avatar.”) If your game needs such a fantastic landscape, it’s great, but if you need a more realistic model, then we need to adjust the fractal function a little. Fortunately, the ScaleDomain function can do this .



We want to make the function behave like a height map function. Imagine a 2D height map, where each point on the map represents the height of a point in the grid of grid points that are raised up or down. White values ​​of the map indicate high hills, black - low valleys. We need similar behavior, but in order to achieve it, we need to essentially get rid of one of the dimensions. In the case of a height map, we create a 3D elevation from a 2D height map. Similarly, in the case of a 2D terrain, we need a 1D height map. Having made so that all points of a fractal with the same Y coordinate have the same value, we can shift all points with the same X coordinate by the same amount, so the flying islands disappear. To do this, you can use ScaleDomain, resetting the scaley coefficient. That is, before calling the ground_shape_fractal function, we call ground_scale_y to set the y coordinate to 0. This ensures that the Y value does not affect the output of the fractal, essentially turning it into a 1D noise function. To do this, we will make the following changes:

 terraintree =
 {
	 {name = "ground_gradient", type = "gradient", x1 = 0, x2 = 0, y1 = 0, y2 = 1},
	 {name = "ground_shape_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 6, frequency = 2},
	 {name = "ground_scale", type = "scaleoffset", scale = 0.5, offset = 0, source = "ground_shape_fractal"},
	 {name = "ground_scale_y", type = "scaledomain", source = "ground_scale", scaley = 0},
	 {name = "ground_perturb", type = "translatedomain", source = "ground_gradient", ty = "ground_scale_y"},
	
	 {name = "ground_select", type = "select", low = 0, high = 1, threshold = 0.5, control = "ground_perturb"}
 }

We chain the ScaleDomain function to ground_scale, and then modify the original ground_perturb data to be a ScaleDomain function. This will change the fractal that displaces the earth and turns it into something similar:









Now if we take a look at the output, we get the result:









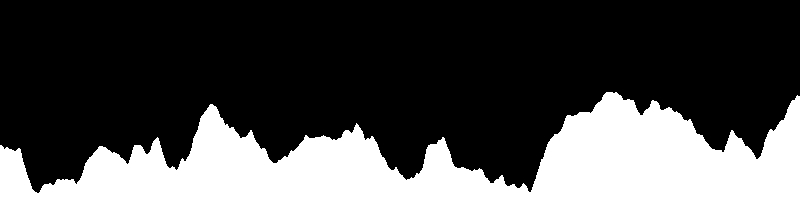
Much better. Flying islands have completely disappeared, and the relief is more like mountains and hills. Unfortunately, we lost protrusions and cliffs. Now the whole earth is continuous and sloping. If you wish, you can fix this in several ways.



First, you can use another TranslateDomain function, coupled with another Fractal function. If we apply a small amount of fractal turbulence to the X direction, we can slightly distort the edges and surfaces of the mountains, and this will probably be enough to form precipices and ledges. Let's look at it in action.

 terraintree =
 {
	 {name = "ground_gradient", type = "gradient", x1 = 0, x2 = 0, y1 = 0, y2 = 1},
	 {name = "ground_shape_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 6, frequency = 2},
	 {name = "ground_scale", type = "scaleoffset", scale = 0.5, offset = 0, source = "ground_shape_fractal"},
	 {name = "ground_scale_y", type = "scaledomain", source = "ground_scale", scaley = 0},
	 {name = "ground_perturb", type = "translatedomain", source = "ground_gradient", ty = "ground_scale_y"},
	 {name = "ground_overhang_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 6, frequency = 2},
	 {name = "ground_overhang_scale", type = "scaleoffset", source = "ground_overhang_fractal", scale = 0.2, offset = 0},
	 {name = "ground_overhang_perturb", type = "translatedomain", source = "ground_perturb", tx = "ground_overhang_scale"},
	
	 {name = "ground_select", type = "select", low = 0, high = 1, threshold = 0.5, control = "ground_overhang_perturb"}
 }

And here is the result:









The second way: you can simply set the scaley parameter of the ground_scale_y function to a value greater than 0. If you leave a small scale in Y, we will get a fraction of the variation, however, the larger the scale, the stronger the relief will resemble the previous version without scaling.









The results look much more interesting than ordinary sloping mountains. However, no matter how interesting they are, the player will still get bored with exploring the relief with the same pattern, stretching for many kilometers. In addition, such a relief will be very unrealistic. In the real world, there is a lot of variability that makes the terrain more interesting. Let's see what can be done to make the world more diverse.



Looking at the previous code example, you can see a specific pattern in it. We have a gradient function, which is controlled by functions that give the earth a shape, after which a piecewise-defined function is applied and the earth becomes full. That is, it will be more logical to complicate the relief at the stage of shaping the earth. Instead of one fractal displacing along Y and another displacing along X, we can achieve the required degree of complexity (taking into account performance: each fractal requires additional computational costs, so we must try to be conservative.) We can specify the forms of the earth, which are mountains, foothills , flat lowlands, wastelands, etc ... and use the output of the various Select functions, combined in chains with low-frequency fractals, to outline areas of each type. So let's see how you can implement different types of terrain.



To illustrate the principle, we distinguish three types of relief: plateaus (smooth sloping hills), mountains and lowlands (mostly flat). To switch between them, we use a select-based system and combine them into a complex canvas. So here we go ...



Foothills:



With them, everything is simple. We can take the scheme used above, slightly reduce the amplitude of the hills, perhaps even make them more subtractive than additive. to lower the average heights. We can also reduce the octave count to smooth them out.

 {name = "lowland_shape_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 2, frequency = 1},
 {name = "lowland_autocorrect", type = "autocorrect", source = "lowland_shape_fractal", low = 0, high = 1},
 {name = "lowland_scale", type = "scaleoffset", source = "lowland_autocorrect", scale = 0.2, offset = -0.25},
 {name = "lowland_y_scale", type = "scaledomain", source = "lowland_scale", scaley = 0},
 {name = "lowland_terrain", type = "translatedomain", source = "ground_gradient", ty = "lowland_y_scale"},

Highlands:



With them, too, everything is simple. (In fact, none of these terrain types is difficult.) However, we use a different basis to make the hills look like dunes.

 {name = "highland_shape_fractal", type = "fractal", fractaltype = anl.RIDGEDMULTI, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 2, frequency = 2},
 {name = "highland_autocorrect", type = "autocorrect", source = "highland_shape_fractal", low = 0, high = 1},
 {name = "highland_scale", type = "scaleoffset", source = "highland_autocorrect", scale = 0.45, offset = 0},
 {name = "highland_y_scale", type = "scaledomain", source = "highland_scale", scaley = 0},
 {name = "highland_terrain", type = "translatedomain", source = "ground_gradient", ty = "highland_y_scale"},

The mountains:

 {name = "mountain_shape_fractal", type = "fractal", fractaltype = anl.BILLOW, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 4, frequency = 1},
 {name = "mountain_autocorrect", type = "autocorrect", source = "mountain_shape_fractal", low = 0, high = 1},
 {name = "mountain_scale", type = "scaleoffset", source = "mountain_autocorrect", scale = 0.75, offset = 0.25},
 {name = "mountain_y_scale", type = "scaledomain", source = "mountain_scale", scaley = 0.1},
 {name = "mountain_terrain", type = "translatedomain", source = "ground_gradient", ty = "mountain_y_scale"},

Of course, you can approach this process even more creatively, but in general the pattern will be like that. We highlight the characteristics of the type of relief and select noise functions for them. For all this, the same principles apply; The main differences are the scale. Now, to connect them together, we will prepare additional fractals that will control the Select function. Then we chain Select modules to generate the entire terrain.

 {name = "terrain_type_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 3, frequency = 0.5},
 {name = "terrain_autocorrect", type = "autocorrect", source = "terrain_type_fractal", low = 0, high = 1},
 {name = "terrain_type_cache", type = "cache", source = "terrain_autocorrect"},
 {name = "highland_mountain_select", type = "select", low = "highland_terrain", high = "mountain_terrain", control = "terrain_type_cache", threshold = 0.55, falloff = 0.15},
 {name = "highland_lowland_select", type = "select", low = "lowland_terrain", high = "highland_mountain_select", control = "terrain_type_cache", threshold = 0.25, falloff = 0.15},

So, here we define three main types of terrain: lowlands, highlands and mountains. We use one fractal to select one of them, so that there are natural transitions (lowlands-> highlands-> mountains). Then we use another fractal to randomly insert badlands into the map. Here's what the finished module chain looks like:

 terraintree =
 {
	 {name = "lowland_shape_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 2, frequency = 1},
	 {name = "lowland_autocorrect", type = "autocorrect", source = "lowland_shape_fractal", low = 0, high = 1},
	 {name = "lowland_scale", type = "scaleoffset", source = "lowland_autocorrect", scale = 0.2, offset = -0.25},
	 {name = "lowland_y_scale", type = "scaledomain", source = "lowland_scale", scaley = 0},
	 {name = "lowland_terrain", type = "translatedomain", source = "ground_gradient", ty = "lowland_y_scale"},
	 {name = "ground_gradient", type = "gradient", x1 = 0, x2 = 0, y1 = 0, y2 = 1},
	 {name = "highland_shape_fractal", type = "fractal", fractaltype = anl.RIDGEDMULTI, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 2, frequency = 2},
	 {name = "highland_autocorrect", type = "autocorrect", source = "highland_shape_fractal", low = 0, high = 1},
	 {name = "highland_scale", type = "scaleoffset", source = "highland_autocorrect", scale = 0.45, offset = 0},
	 {name = "highland_y_scale", type = "scaledomain", source = "highland_scale", scaley = 0},
	 {name = "highland_terrain", type = "translatedomain", source = "ground_gradient", ty = "highland_y_scale"},

	 {name = "mountain_shape_fractal", type = "fractal", fractaltype = anl.BILLOW, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 4, frequency = 1},
	 {name = "mountain_autocorrect", type = "autocorrect", source = "mountain_shape_fractal", low = 0, high = 1},
	 {name = "mountain_scale", type = "scaleoffset", source = "mountain_autocorrect", scale = 0.75, offset = 0.25},
	 {name = "mountain_y_scale", type = "scaledomain", source = "mountain_scale", scaley = 0.1},
	 {name = "mountain_terrain", type = "translatedomain", source = "ground_gradient", ty = "mountain_y_scale"},

	 {name = "terrain_type_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 3, frequency = 0.5},
	 {name = "terrain_autocorrect", type = "autocorrect", source = "terrain_type_fractal", low = 0, high = 1},
	 {name = "terrain_type_cache", type = "cache", source = "terrain_autocorrect"},
	 {name = "highland_mountain_select", type = "select", low = "highland_terrain", high = "mountain_terrain", control = "terrain_type_cache", threshold = 0.55, falloff = 0.15},
	 {name = "highland_lowland_select", type = "select", low = "lowland_terrain", high = "highland_mountain_select", control = "terrain_type_cache", threshold = 0.25, falloff = 0.15},
	 {name = "ground_select", type = "select", low = 0, high = 1, threshold = 0.5, control = "highland_lowland_select"}
 }

Here are some examples of the resulting reliefs:





















You may notice that a rather high variability is obtained. In some places, towering broken mountains appear, in others there are smooth sloping plains. Now we need to add caves so that we can explore the wonders of the underworld.



For caves, I use the multiplicative system applied to ground_select . That is, I create a function that outputs 1 or 0, and multiply them by the output of ground_select . Thanks to this, any point of the function becomes hollow for which the value of the function of the caves is 0. That is, where I want to get the cave, the function of the caves should return 0, and where the cave should not be, the function should be 1. As for the shape caves, I want to establish a cave system based on the 1-octave Ridged Multifractal .

 {name = "cave_shape", type = "fractal", fractaltype = anl.RIDGEDMULTI, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 1, frequency = 2},

The result is something like this:









If we apply the Select function as a piecewise-defined function, as we did with the earth gradient, implementing it so that the lower part of the select threshold is 1 (no cave), and the upper part is 0 (there is a cave), the result will look something like this :

 {name = "cave_shape", type = "fractal", fractaltype = anl.RIDGEDMULTI, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 1, frequency = 2},
 {name = "cave_select", type = "select", low = 1, high = 0, control = "cave_shape", threshold = 0.8, falloff = 0},

Result:









Of course, it looks pretty smooth, so let's add some fractal noise to distort the area.

 {name = "cave_shape", type = "fractal", fractaltype = anl.RIDGEDMULTI, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 1, frequency = 2},
 {name = "cave_select", type = "select", low = 1, high = 0, control = "cave_shape", threshold = 0.8, falloff = 0},
 {name = "cave_perturb_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 6, frequency = 3},
 {name = "cave_perturb_scale", type = "scaleoffset", source = "cave_perturb_fractal", scale = 0.25, offset = 0},
 {name = "cave_perturb", type = "translatedomain", source = "cave_select", tx = "cave_perturb_scale"},

Result:









This makes the caves slightly noisy and makes them not so smooth. Let's now see what happens if you apply the caves to the relief:









By experimenting with the threshold value in cave_select , we can make the caves thinner or thicker. But the main thing that we need to try is to make sure that the caves do not eat away such huge fragments of the surface relief. To do this, we can return to the highland_lowland_select function , which, as we recall, is the last relief function that distorts the gradient of the earth. What is useful in this function is that it is still a gradient, increasing the value when the function deepens into the ground. We can use the gradient to weaken the function of the caves so that the caves increase as they go deeper into the ground. Fortunately for us, this attenuation can be achieved simply by multiplying the output of the highland_lowland_select functionto the output of cave_shape , and then pass the result to the rest of the function chain. Next, we will make an important change here - add the Cache function . The caching function saves the result of the function for the given incoming coordinate, and if the function is called repeatedly with the same coordinate, it will return the cached copy, and will not calculate the result again. This is useful in situations like this, when one complex function ( highland_lowland_select ) in a function chain is called several times. Without a cache, the entire chain of a complex function is recalculated with every call. To add the cache, we first need to make the following changes:

{name = "highland_lowland_select", type = "select", low = "lowland_terrain", high = "highland_mountain_select", control = "terrain_type_cache", threshold = 0.25, falloff = 0.15},
{name = "highland_lowland_select_cache", type = "cache", source = "highland_lowland_select"},
{name = "ground_select", type = "select", low = 0, high = 1, threshold = 0.5, control = "highland_lowland_select_cache"},

So we added Cache and then redirected the input to ground_select so that it was taken from the cache and not directly from the function. Then we can change the cave code to add attenuation:

{name = "cave_shape", type = "fractal", fractaltype = anl.RIDGEDMULTI, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 1, frequency = 4},
{name="cave_attenuate_bias", type="bias", source="highland_lowland_select_cache", bias=0.45},
{name="cave_shape_attenuate", type="combiner", operation=anl.MULT, source_0="cave_shape", source_1="cave_attenuate_bias"},
{name="cave_perturb_fractal", type="fractal", fractaltype=anl.FBM, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=6, frequency=3},
{name="cave_perturb_scale", type="scaleoffset", source="cave_perturb_fractal", scale=0.5, offset=0},
{name="cave_perturb", type="translatedomain", source="cave_shape_attenuate", tx="cave_perturb_scale"},
{name="cave_select", type="select", low=1, high=0, control="cave_perturb", threshold=0.48, falloff=0},

First of all, we added the Bias function . This is for convenience, because it allows us to adjust the interval of the gradient attenuation function. Then the cave_shape_attenuate function is added , which is a Combiner of type anl :: MULT . She multiplies the gradient by cave_shape . Then the result of this operation is passed to the cave_perturb function . The result looks something like this:









We see that closer to the surface of the earth have become thinner. (Don’t pay attention to the very top, this is just an artifact of negative gradient values, it does not affect the finished caves. If this becomes a problem - let's say if we use this function for something else, then we can limit the gradient to the interval (0, 1).) It's a little hard to see how this works in relation to the terrain, so let's move on and put everything together to see what happens. Here is the whole chain of functions that we have created so far.

terraintree =
 {
	{name = "ground_gradient", type = "gradient", x1 = 0, x2 = 0, y1 = 0, y2 = 1},
	
	{name = "lowland_shape_fractal", type = "fractal", fractaltype = anl.BILLOW, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 2, frequency = 0.25},
	{name="lowland_autocorrect", type="autocorrect", source="lowland_shape_fractal", low=0, high=1},
	{name="lowland_scale", type="scaleoffset", source="lowland_autocorrect", scale=0.125, offset=-0.45},
	{name="lowland_y_scale", type="scaledomain", source="lowland_scale", scaley=0},
	{name="lowland_terrain", type="translatedomain", source="ground_gradient", ty="lowland_y_scale"},
	
	{name="highland_shape_fractal", type="fractal", fractaltype=anl.FBM, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=4, frequency=2},
	{name="highland_autocorrect", type="autocorrect", source="highland_shape_fractal", low=-1, high=1},
	{name="highland_scale", type="scaleoffset", source="highland_autocorrect", scale=0.25, offset=0},
	{name="highland_y_scale", type="scaledomain", source="highland_scale", scaley=0},
	{name="highland_terrain", type="translatedomain", source="ground_gradient", ty="highland_y_scale"},

	{name="mountain_shape_fractal", type="fractal", fractaltype=anl.RIDGEDMULTI, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=8, frequency=1},
	{name="mountain_autocorrect", type="autocorrect", source="mountain_shape_fractal", low=-1, high=1},
	{name="mountain_scale", type="scaleoffset", source="mountain_autocorrect", scale=0.45, offset=0.15},
	{name="mountain_y_scale", type="scaledomain", source="mountain_scale", scaley=0.25},
	{name="mountain_terrain", type="translatedomain", source="ground_gradient", ty="mountain_y_scale"},

	{name="terrain_type_fractal", type="fractal", fractaltype=anl.FBM, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=3, frequency=0.125},
	{name="terrain_autocorrect", type="autocorrect", source="terrain_type_fractal", low=0, high=1},
	{name="terrain_type_y_scale", type="scaledomain", source="terrain_autocorrect", scaley=0},
	{name="terrain_type_cache", type="cache", source="terrain_type_y_scale"},
	{name="highland_mountain_select", type="select", low="highland_terrain", high="mountain_terrain", control="terrain_type_cache", threshold=0.55, falloff=0.2},
	{name="highland_lowland_select", type="select", low="lowland_terrain", high="highland_mountain_select", control="terrain_type_cache", threshold=0.25, falloff=0.15},
	{name="highland_lowland_select_cache", type="cache", source="highland_lowland_select"},
	{name="ground_select", type="select", low=0, high=1, threshold=0.5, control="highland_lowland_select_cache"},
	
	{name="cave_shape", type="fractal", fractaltype=anl.RIDGEDMULTI, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=1, frequency=4},
	{name="cave_attenuate_bias", type="bias", source="highland_lowland_select_cache", bias=0.45},
	{name="cave_shape_attenuate", type="combiner", operation=anl.MULT, source_0="cave_shape", source_1="cave_attenuate_bias"},
	{name="cave_perturb_fractal", type="fractal", fractaltype=anl.FBM, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=6, frequency=3},
	{name="cave_perturb_scale", type="scaleoffset", source="cave_perturb_fractal", scale=0.5, offset=0},
	{name="cave_perturb", type="translatedomain", source="cave_shape_attenuate", tx="cave_perturb_scale"},
	{name="cave_select", type="select", low=1, high=0, control="cave_perturb", threshold=0.48, falloff=0},
	
	{name = "ground_cave_multiply", type = "combiner", operation = anl.MULT, source_0 = "cave_select", source_1 = "ground_select"}
 }

Here are examples of randomized cards derived from this function:





















Now everything looks pretty good. All caves are rather large caverns deep underground, but closer to the surface they usually turn into small tunnels. This helps create an atmosphere of mystery. Exploring the surface, you find a small entrance to the cave. Where is she going? How deep does it extend? We cannot know this, but in the process of studying it begins to expand, turning into an extensive system of caverns filled with darkness and dangers. And loot, of course. There is always a lot of loot.



You can change this system in many different ways, getting different results. We can change threshold parameters for cave_select and parameters for cave_attenuate_bias , or replace cave_attenuate_biasother functions to match the gradient interval to other values ​​that better suit your needs. You can also add another fractal, distorting the cave system along the Y axis, to eliminate the possibility of unnaturally smooth tunnels along the X axis (caused by the fact that the cave shape is distorted only along the X axis). You can also add a new fractal as an additional source of attenuation, specify a third source for cave_shape_attenuate , which scales the attenuation based on regions, so that caves in some areas are denser (for example, in the mountains), and less often or completely absent in others. This regional select can be created from the terrain_type_fractal functionto know where the areas of the mountains are located. It all comes down to just thinking over what you want, figuring out what effect different functions will have on the output, and experimenting with the parameters until you get the desired result. This is not an exact science, and often the desired effect can be reached in different ways.

disadvantages

This terrain generation method has drawbacks. The noise generation process can be quite slow. It is important to reduce the number of fractals, the number of octaves of those fractals that you use, and other slow operations, if possible. Try to use fractals multiple times and cache all functions that are called multiple times. In this example, I freely used fractals, creating one for each of the three relief types. Using ScaleOffset to change the intervals and taking one fractal as the basis for them all, I would save a lot of processor time. In 2D, everything is not so bad, but when you get to 3D and try to compare the amounts of data, the processing time will increase significantly.

Go to 3D

All this is great if you create a game like Terraria or King Arthur's Gold , but what if you need something like Minecraft or Infiniminer? What changes will we need to make to the function chain? In fact, there are not many. The function shown above with almost no modifications will work for 3D relief. It will be enough for you to compare the 3D volume using the 3D variations of the generator, and also to compare the Y axis with the vertical axis of the volume, and not the 2D region. However, one change will nevertheless be required, namely, a way to realize the caves. As you saw, Ridged Multifractal is great for a 2D cave system, but in 3D it cuts out a lot of curved shells, not tunnels, and its effect turns out to be wrong. That is, in 3D it is necessary to specify two fractal forms of caves, both are 1-octave Ridged Multifractal noise, but with different seeds. Using Select, set them to 1 or 0, and multiply them. Thus, at the intersection of fractals, a cave will appear,and everything else will remain solid, and the appearance of the tunnels will become more natural than using a single fractal.

terraintree3d=
 {
	{name="ground_gradient", type="gradient", x1=0, x2=0, y1=0, y2=1},
	
	{name="lowland_shape_fractal", type="fractal", fractaltype=anl.BILLOW, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=2, frequency=0.25},
	{name="lowland_autocorrect", type="autocorrect", source="lowland_shape_fractal", low=0, high=1},
	{name="lowland_scale", type="scaleoffset", source="lowland_autocorrect", scale=0.125, offset=-0.45},
	{name="lowland_y_scale", type="scaledomain", source="lowland_scale", scaley=0},
	{name="lowland_terrain", type="translatedomain", source="ground_gradient", ty="lowland_y_scale"},
	
	{name="highland_shape_fractal", type="fractal", fractaltype=anl.FBM, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=4, frequency=2},
	{name="highland_autocorrect", type="autocorrect", source="highland_shape_fractal", low=-1, high=1},
	{name="highland_scale", type="scaleoffset", source="highland_autocorrect", scale=0.25, offset=0},
	{name="highland_y_scale", type="scaledomain", source="highland_scale", scaley=0},
	{name="highland_terrain", type="translatedomain", source="ground_gradient", ty="highland_y_scale"},

	{name="mountain_shape_fractal", type="fractal", fractaltype=anl.RIDGEDMULTI, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=8, frequency=1},
	{name="mountain_autocorrect", type="autocorrect", source="mountain_shape_fractal", low=-1, high=1},
	{name="mountain_scale", type="scaleoffset", source="mountain_autocorrect", scale=0.45, offset=0.15},
	{name="mountain_y_scale", type="scaledomain", source="mountain_scale", scaley=0.25},
	{name="mountain_terrain", type="translatedomain", source="ground_gradient", ty="mountain_y_scale"},

	{name="terrain_type_fractal", type="fractal", fractaltype=anl.FBM, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=3, frequency=0.125},
	{name="terrain_autocorrect", type="autocorrect", source="terrain_type_fractal", low=0, high=1},
	{name="terrain_type_y_scale", type="scaledomain", source="terrain_autocorrect", scaley=0},
	{name="terrain_type_cache", type="cache", source="terrain_type_y_scale"},
	{name="highland_mountain_select", type="select", low="highland_terrain", high="mountain_terrain", control="terrain_type_cache", threshold=0.55, falloff=0.2},
	{name="highland_lowland_select", type="select", low="lowland_terrain", high="highland_mountain_select", control="terrain_type_cache", threshold=0.25, falloff=0.15},
	{name="highland_lowland_select_cache", type="cache", source="highland_lowland_select"},
	{name="ground_select", type="select", low=0, high=1, threshold=0.5, control="highland_lowland_select_cache"},
	
	{name="cave_attenuate_bias", type="bias", source="highland_lowland_select_cache", bias=0.45},
	{name="cave_shape1", type="fractal", fractaltype=anl.RIDGEDMULTI, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=1, frequency=4},
	{name="cave_shape2", type="fractal", fractaltype=anl.RIDGEDMULTI, basistype=anl.GRADIENT, interptype=anl.QUINTIC, octaves=1, frequency=4},
	{name="cave_shape_attenuate", type="combiner", operation=anl.MULT, source_0="cave_shape1", source_1="cave_attenuate_bias", source_2="cave_shape2"},             
	{name = "cave_perturb_fractal", type = "fractal", fractaltype = anl.FBM, basistype = anl.GRADIENT, interptype = anl.QUINTIC, octaves = 6, frequency = 3},
	{name = "cave_perturb_scale", type = "scaleoffset", source = "cave_perturb_fractal", scale = 0.5, offset = 0},
	{name = "cave_perturb", type = "translatedomain", source = "cave_shape_attenuate", tx = "cave_perturb_scale"},
	{name = "cave_select", type = "select", low = 1, high = 0, control = "cave_perturb", threshold = 0.48, falloff = 0},
	
	{name = "ground_cave_multiply", type = "combiner", operation = anl.MULT, source_0 = "cave_select", source_1 = "ground_select"}
 }

Examples of results:















It seems that some of the settings require tuning. It may be worth reducing the attenuation or making the caves thinner, reducing the number of octaves in the fractal of the relief, so that the relief becomes smoother, etc. ... I repeat, it all depends on what result you want to get.