I went into the study of collision recognition processes, and this led me to the Gilbert-Johnson-Keerthi (GJK) algorithm.
All code examples in the post are written in TypeScript. The examples use the structures I created that are not discussed in detail in the post. They are simple and can be viewed in the GitHub repository:
Vector
-
IShape
-
Collision
All code from the post is stored in the GitHub repository:
https://github.com/jthomperoo/gjk-ts-implementation
The post was written on the basis of this article and the video recommended in it:
Introduction
GJK is an algorithm designed to determine the intersection of two convex shapes. It is simple and implemented using a generalized “auxiliary function” that allows you to use a more general approach - in the same way, you can process polygons and shapes, consisting of curves, for example, ellipses.
Required Information
Minkowski sum
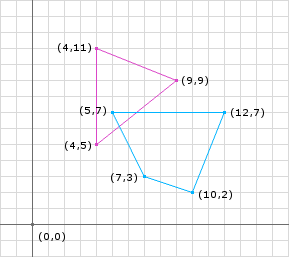
GJK uses a concept called the Minkowski sum. SM is calculated by adding up all the points of two figures. For example, take the two figures shown below:
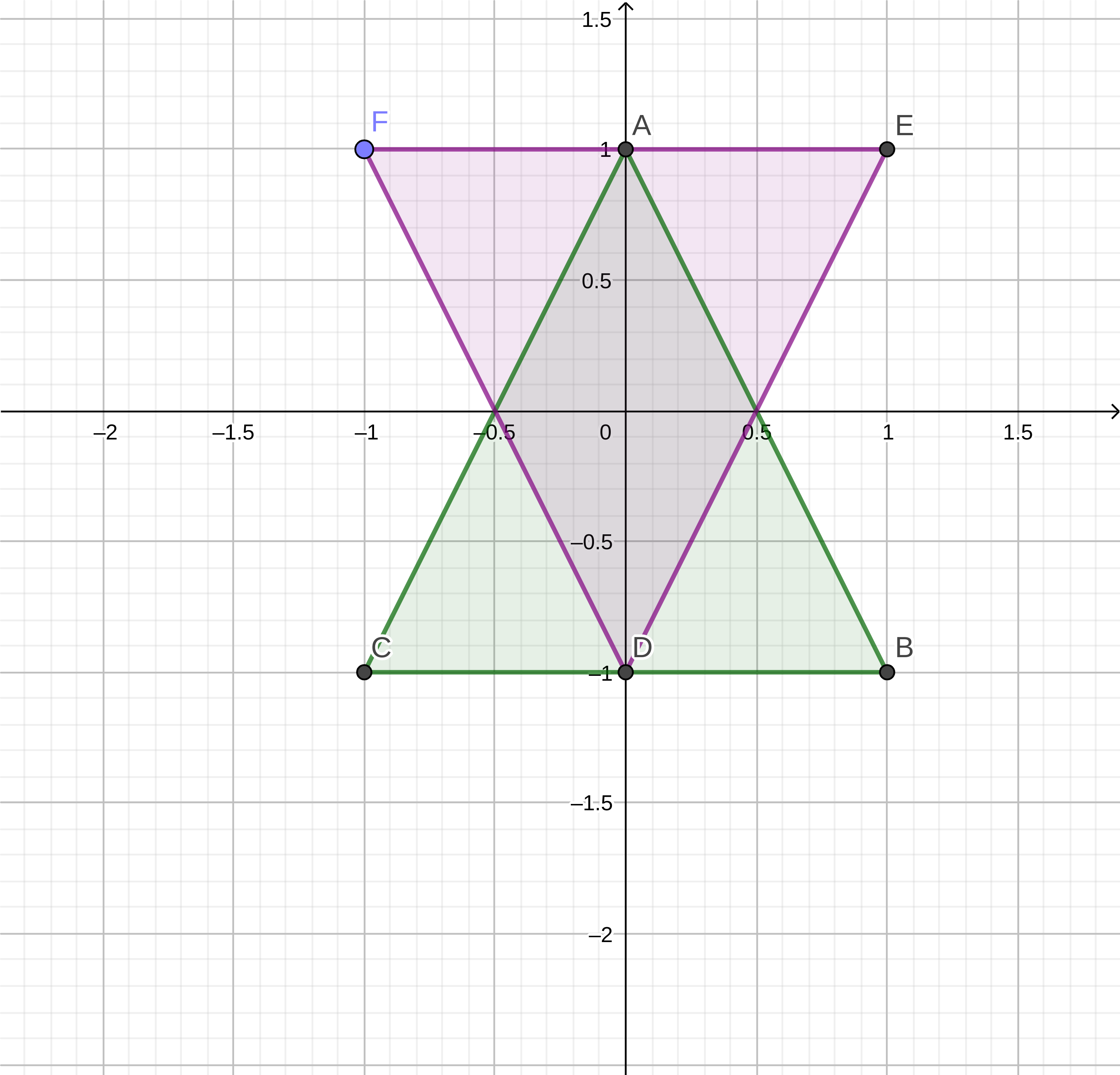
Figure A (green):
| A | B | C |
|---|---|---|
| (0,1) | (1, -1) | (-1, -1) |
Figure B (purple):
| D | E | F |
|---|---|---|
| (0, -1) | (1,1) | (-1.1) |
Taking the values of figure A and figure B, we can calculate the Minkowski sum:
A + D = (0,1) + (0,-1) = (0,0)
A + E = (0,1) + (1,1) = (1,2)
A + F = (0,1) + (-1,1) = (-1,2)
B + D = (1,-1) + (0,-1) = (1,-2)
B + E = (1,-1) + (1,1) = (2,0)
B + F = (1,-1) + (-1,1) = (0,0)
C + D = (-1,-1) + (0,-1) = (-1,-2)
C + E = (-1,-1) + (1,1) = (0,0)
C + F = (-1,-1) + (-1,1) = (-2,0)
If we take these values and draw a graph from them, we will see which figure will be the result.
Minkowski sum for figures A and B:
Note that AD in the table and graph corresponds to A + D
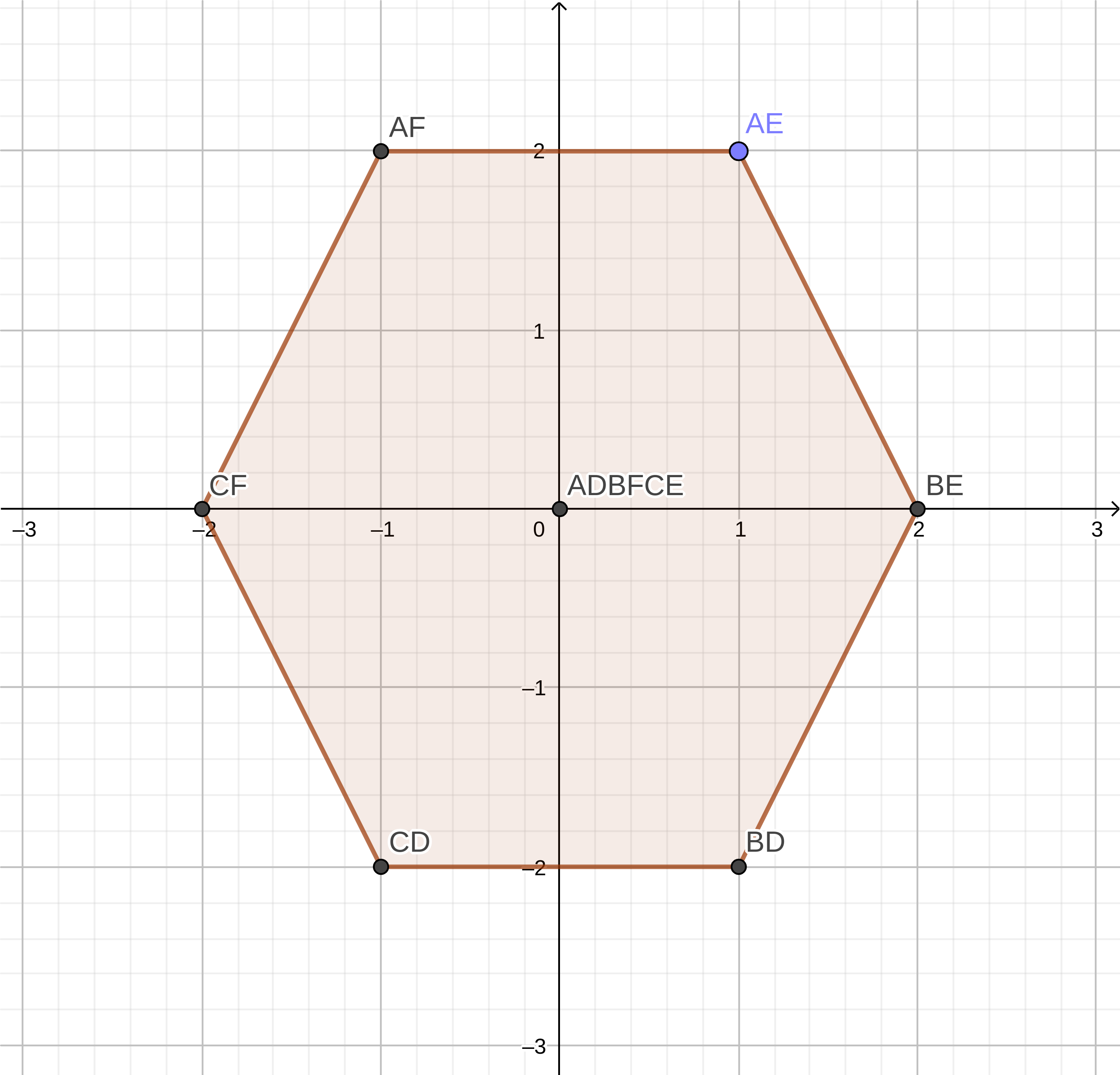
| AD | Ae | AF | Bd | BE | Bf | CD | CE | CF |
|---|---|---|---|---|---|---|---|---|
| (0,0) | (1,2) | (-1.2) | (1, -2) | (2.0) | (0,0) | (-1, -2) | (0,0) | (-2.0) |
To better understand the Minkowski sum, we can imagine that we take a figure A and bypass it with the outline of a B. The resulting figure will be the Minkowski sum.
Minkowski difference
GJK uses a variation of the Minkowski sum in which it is taken not A + B, but A - B. In the sources I read, this is called the “Minkowski Difference”. The Minkowski difference has an interesting property: if two figures overlap / intersect, then the resulting Minkowski difference will contain the origin. And this is the basis of the GJK algorithm.
Taking the values of figures A and B, we can calculate the Minkowski difference:
A - D = (0,1) - (0,-1) = (0,2)
A - E = (0,1) - (1,1) = (-1,0)
A - F = (0,1) - (-1,1) = (1,0)
B - D = (1,-1) - (0,-1) = (-1,0)
B - E = (1,-1) - (1,1) = (0,-2)
B - F = (1,-1) - (-1,1) = (2,-2)
C - D = (-1,-1) - (0,-1) = (-1,0)
C - E = (-1,-1) - (1,1) = (-2,-2)
C - F = (-1,-1) - (-1,1) = (0,-2)
If we take these values and put them on the graph, we will see the resulting figure.
Minkowski difference for figures A and B:
Note that AD in the table and graph refers to A - D
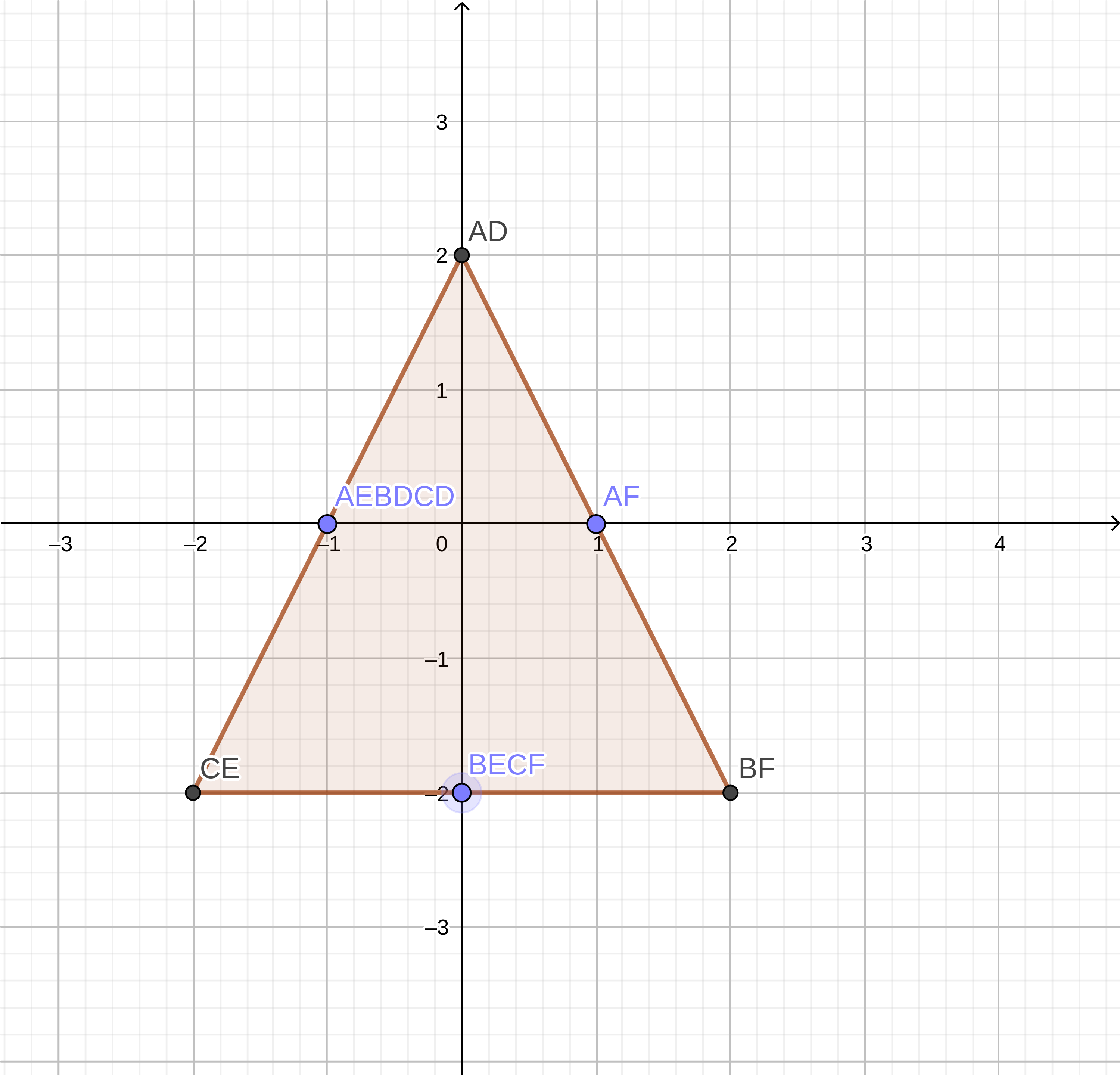
| AD | Ae | AF | Bd | BE | Bf | CD | CE | CF |
|---|---|---|---|---|---|---|---|---|
| (0.2) | (-1.0) | (1,0) | (-1.0) | (0, -2) | (2, -2) | (-1.0) | (-2, -2) | (0, -2) |
Algorithm
Based on these concepts, the GJK algorithm optimizes them. Calculating the Minkowski sum can take a lot of time, especially if you check the intersection of two figures consisting of many points. To avoid this, GJK uses two key concepts: helper functions and simplexes.
Secondary functions
Auxiliary functions are a way of sampling a point on the edge of the Minkowski difference without constructing the entire figure. The helper function gets two compared figures, and the direction that needs to be checked. Then the auxiliary function receives from each figure a point farthest from two opposite directions. Using these two most distant points, you can calculate the auxiliary point on the figure of the Minkowski difference. We take points from opposite directions because we get a point on the Minkowski difference, which will give us the largest area, that is, there will be a higher probability that we will enclose the origin in the figure. Since the Minkowski difference is the
a - b
, the presence of the point of the figure b sampled from the opposite direction will give us an auxiliary point that is as far as possible in this direction.
The implementation of the helper function is quite simple:
function support(a: IShape, b: IShape, direction: Vector): Vector { const aFar = a.FarthestPointInDirection(direction); const bFar = b.FarthestPointInDirection(direction.Invert()); return aFar.Sub(bFar); }
One of the advantages of GJK is that
FarthestPointInDirection
can be abstracted and applied to polygons and curves. Here is the implementation of
FarthestPointInDirection
for a polygon.
class Polygon implements IShape { public points: Vector[]; ... public FarthestPointInDirection(direction: Vector): Vector { let farthestDistance = -Infinity; // If there are no points, just return point 0,0 let farthestPoint: Vector = new Vector(0,0); for (const point of this.points) { const distanceInDirection = point.Dot(direction); if (distanceInDirection > farthestDistance) { farthestPoint = point; farthestDistance = distanceInDirection; } } return farthestPoint; } }
If you want to see how other shapes will be implemented, then check out the Git repository of this post , which introduces the implementation for
Circle
.
Here's how the auxiliary point in the (1,0) direction will be calculated for figures A and B:
- Take the most distant point from the figure A; it turns out to be point B (1, -1) . (It can be calculated, as the algorithm shown above does, or simply seen by looking at the graph).
- Take the most distant point from figure B; it turns out to be the point F (-1, 1) .
- Calculate B - F ; it turns out to be point BF (2, -2) - it will be auxiliary .
Simplexes
A simplex is a sample of points along the figure of the Minkowski difference. Simplexes can contain up to three points. GJK uses them, trying to construct a triangle around the origin to determine the occurrence of a collision.
Simplex construction
Simplexes are constructed iteratively by adding auxiliary points in different directions. Each auxiliary point should point in a new direction, so that we can as quickly as possible build a simplex containing a point of origin. The difficulty lies in choosing the direction in which to get the next auxiliary point.
Collision detection and direction selection
The basic algorithm simply builds a simplex using an auxiliary function, trying to enclose a point of origin in the figure. We can understand that there is no collision / intersection by checking whether the calculated auxiliary point reaches the origin, and if it does not, then the origin must be outside the Minkowski difference; therefore, we can say that there is no collision / intersection.
function Calculate(a: IShape, b: IShape): Collision | undefined { // Build a new Simplex for determining if a collision has occurred const simplex = new Simplex(); // Choose an arbitrary starting direction let direction: Vector | undefined = new Vector(0,1); // Get the first support point and add it to the simplex const initSupportPoint = support(a, b, direction); simplex.Add(initSupportPoint); // Flip the direction for the next support point direction = direction.Invert(); // Keep iterating until the direction is undefined, this will occur when // 'CalculateDirection' doesn't return a direction, indicating that an // intersection has been detected while(direction) { const supportPoint = support(a, b, direction); // If the support point did not reach as far as the origin, // the simplex must not contain the origin and therefore there is no // intersection if (supportPoint.Dot(direction!) <= 0) { // No intersection return; } // Add the simplex and determine a new direction simplex.Add(supportPoint); direction = simplex.CalculateDirection(); } // No direction calculated, intersection detected return new Collision(a, b); }
All the complexity and internal workings of the algorithm are in
simplex.CalculateDirection
. This function determines whether the origin is in the current simplex - if so, it will return
undefined
; otherwise, it will return a new direction to obtain an auxiliary point, which must be added to the simplex.
class Simplex { private points: Vector[]; ... CalculateDirection(): Vector | undefined { // Get a, the last point added to the simplex const a = this.points[this.points.length - 1]; // Since a was just added, we know that the inverse of a points // towards the origin const ao = a.Invert(); // If the simplex is a triangle if (this.points.length == 3) { // B is the penultimate in the simplex // C is the oldest point in the simplex const b = this.points[1]; const c = this.points[0]; // Determine a->b and a->c lines const ab = b.Sub(a); const ac = c.Sub(a); // Determine perpendicular of the a->b line let abPerp = new Vector(ab.y, -ab.x); // Check the handedness of the perpendicular, it should // face AWAY from the simplex if (abPerp.Dot(c) >= 0) { abPerp = abPerp.Invert(); } // If the origin lies outside of the simplex remove the // point and determine a new direction in the direction // of the perpendicular; aiming to try to encapsulate // the origin that lies outside if (abPerp.Dot(ao) > 0) { this.points.splice(0, 1); return abPerp; } // Determine perpendicular of the a->c line let acPerp = new Vector(ac.y, -ac.x); // Check the handedness of the perpendicular, it should // face AWAY from the simplex if (acPerp.Dot(b) >= 0) { acPerp = acPerp.Invert(); } // If the origin lies outside of the simplex remove the // point and determine a new direction in the direction // of the perpendicular; aiming to try to encapsulate // the origin that lies outside if (acPerp.Dot(ao) > 0) { this.points.splice(1, 1); return acPerp; } return undefined; } // Otherwise the simplex is just a line // B is the penultimate point in the simplex, // in this case the other end of the line const b = this.points[0]; // Determine a -> b line const ab = b.Sub(a); // Get the perpendicular of the a->b line let abPerp = new Vector(ab.y, -ab.x); // Check the handedness of the perpendicular, it should // face TOWARDS the origin if (abPerp.Dot(ao) <= 0) { abPerp = abPerp.Invert(); } return abPerp; } }
You may wonder: why are we not checking the BC segment? Because we can unconditionally exclude that the origin is along its perpendicular. Since points B and C are already in the simplex, and they have not only been added, we know that they were checked in the previous iteration. They could be checked either as part of a triangle, or as a segment of the first two points in a simplex - it does not matter. Therefore, we can safely skip checking BC.
Detailed explanation
We got a lot of code, and it looks confusing. Below I will go through the steps for all the steps of the algorithm for the above figures A and B.
Points of figures A and B:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| (0,1) | (1, -1) | (-1, -1) | (0, -1) | (1,1) | (-1.1) |
- Preparation of the algorithm; we take
(0,1)
as the initial direction.
// Build a new Simplex for determining if a collision has occurred const simplex = new Simplex(); // Choose an arbitrary starting direction let direction: Vector | undefined = new Vector(0,1);
- We get the first auxiliary point.
// Get the first support point and add it to the simplex const initSupportPoint = support(a, b, direction); simplex.Add(initSupportPoint); // Flip the direction for the next support point direction = direction.Invert();
We get the farthest point from point A in the direction(0,1)
and from point B in the direction(0,-1)
.
aFar:(0,1)
and bFar:(0,-1)
Use these values to get the auxiliary point.
Support: aFar-bFar =(0,2)
function support(a: IShape, b: IShape, direction: Vector): Vector { const aFar = a.FarthestPointInDirection(direction); const bFar = b.FarthestPointInDirection(direction.Invert()); return aFar.Sub(bFar); }
- We flip the direction for the next auxiliary point and begin iteration, calculating a new auxiliary point.
Support:(0,-3)
// Flip the direction for the next support point direction = direction.Invert(); // Keep iterating until the direction is undefined, this will occur when // 'CalculateDirection' doesn't return a direction, indicating that an // intersection has been detected while(direction) { const supportPoint = support(a, b, direction);
- Check if the auxiliary point has reached the origin; if not, there should be no intersection. If she reached the origin, then add the point to the simplex.
In this case, the auxiliary point has reached the origin.
direction:(0,-1)
Support:(0,-3)
supportPoint.Dot (direction):3
// If the support point did not reach as far as the origin, // the simplex must not contain the origin and therefore there is no // intersection if (supportPoint.Dot(direction!) <= 0) { // No intersection return; } // Add the simplex and determine a new direction simplex.Add(supportPoint);
- At this stage, the simplex is a segment, so it cannot contain a point of origin inside; define a new direction in which to look for the auxiliary point.
direction = simplex.CalculateDirection();
- We take the last point added to the simplex and determine the direction to the point of origin, this will be the reciprocal of this point.
a:(0,-3)
ao:(0,3)
CalculateDirection(): Vector | undefined { // Get a, the last point added to the simplex const a = this.points[this.points.length - 1]; // Since a was just added, we know that the inverse of a points // towards the origin const ao = a.Invert(); // If the simplex is a triangle if (this.points.length == 3) {
- Since the simplex is a segment, not a triangle, we take the second point of the segment and calculate the segment of the simplex.
b:(0,2)
ab:(0,5)
// Otherwise the simplex is just a line // B is the penultimate point in the simplex, // in this case the other end of the line const b = this.points[0]; // Determine a -> b line const ab = b.Sub(a);
- We compute the perpendicular to this segment and verify that it is directed to the origin. This will be a new direction for the next auxiliary point.
abPerp:(5, 0)
abPerp.Dot (ao)0
abPerp:(-5, 0)
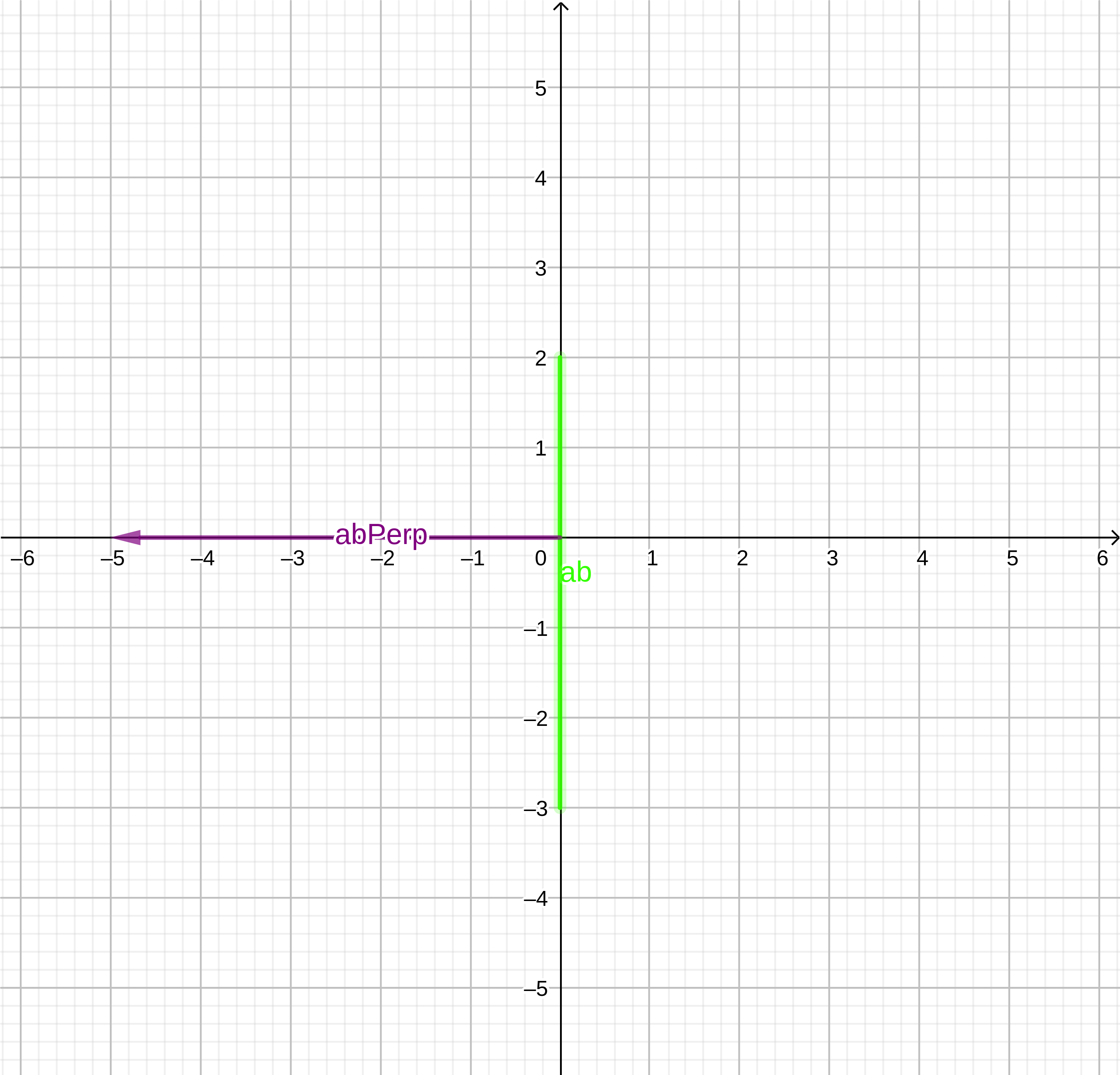
// Get the perpendicular of the a->b line let abPerp = new Vector(ab.y, -ab.x); // Check the handedness of the perpendicular, it should // face TOWARDS the origin if (abPerp.Dot(ao) <= 0) { abPerp = abPerp.Invert(); } return abPerp;
- We take the last point added to the simplex and determine the direction to the point of origin, this will be the reciprocal of this point.
- Now we have a direction to search for the next auxiliary point. We return to the beginning of the cycle and do not exit it, because for now we have a direction, and the intersection has not yet been found.
direction:(-5, 0)
Support:(-2,-2)
supportPoint.Dot (direction):10
The auxiliary point has reached the origin, so we cannot say that there is no intersection.
while(direction) { const supportPoint = support(a, b, direction); // If the support point did not reach as far as the origin, // the simplex must not contain the origin and therefore there is no // intersection if (supportPoint.Dot(direction!) <= 0) { // No intersection return; }
- Add a new auxiliary point to the simplex, creating a triangle. This triangle may contain the origin, and if so, then the simplex will return
undefined
, and not a new direction for the search.
// Add the simplex and determine a new direction simplex.Add(supportPoint); direction = simplex.CalculateDirection();
- Take the points of the simplex of the triangle.
a:(-2,-2)
b:(0,-3)
c:(0,2)
ao:(2,2)
// Get a, the last point added to the simplex const a = this.points[this.points.length - 1]; // Since a was just added, we know that the inverse of a points // towards the origin const ao = a.Invert(); // If the simplex is a triangle if (this.points.length == 3) { // B is the penultimate in the simplex // C is the oldest point in the simplex const b = this.points[1]; const c = this.points[0];
- Take the segments ab and ac.
ab:(2,-1)
ac:(2,4)
// Determine a->b and a->c lines const ab = b.Sub(a); const ac = c.Sub(a);
- We compute the perpendicular to the segment ab, directed from the simplex.
abperp:(-1,-2)
// Determine perpendicular of the a->b line let abPerp = new Vector(ab.y, -ab.x); // Check the handedness of the perpendicular, it should // face AWAY from the simplex if (abPerp.Dot(c) >= 0) { abPerp = abPerp.Invert(); }
- We determine whether the origin is outside the simplex beyond ab.
abPerp.Dot (ao):-6
The origin does not lie outside the simplex beyond ab.
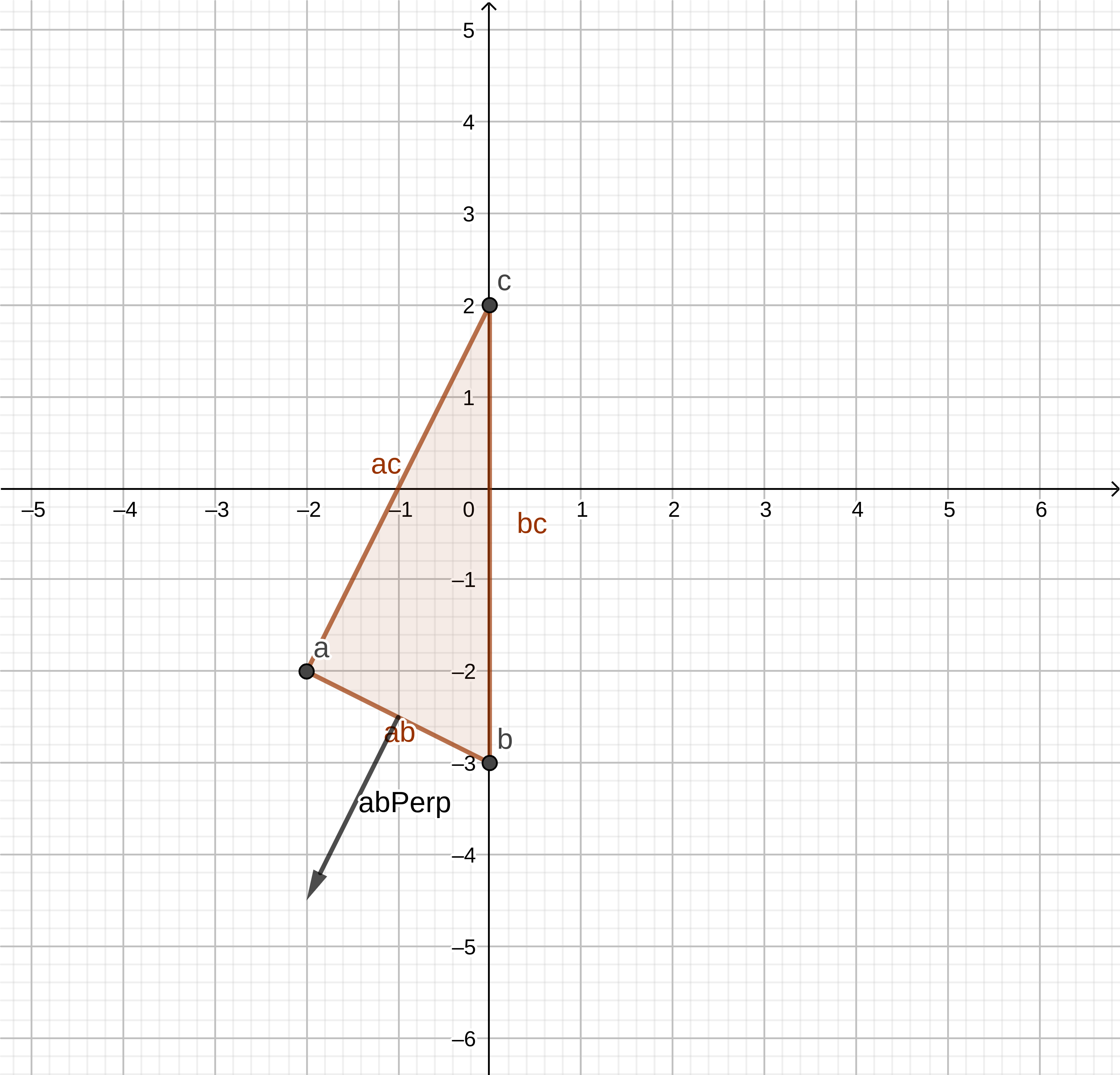
if (abPerp.Dot(ao) > 0) { this.points.splice(0, 1); return abPerp; }
- We compute the perpendicular to the segment ac directed from the simplex.
acPerp:(-4,2)
// Determine perpendicular of the a->c line let acPerp = new Vector(ac.y, -ac.x); // Check the handedness of the perpendicular, it should // face AWAY from the simplex if (acPerp.Dot(b) >= 0) { acPerp = acPerp.Invert(); }
- Determine whether the origin is outside the simplex beyond ac.
acPerp.Dot (ao):-4
The origin is not outside the simplex beyond ab.

// If the origin lies outside of the simplex remove the // point and determine a new direction in the direction // of the perpendicular; aiming to try to encapsulate // the origin that lies outside if (acPerp.Dot(ao) > 0) { this.points.splice(1, 1); return acPerp; }
- Since AB and AC were checked in this iteration, and we know that BC was checked in the previous iteration, the origin must lie inside the simplex, so a collision / intersection was detected - informing about this, the function will return
undefined
.
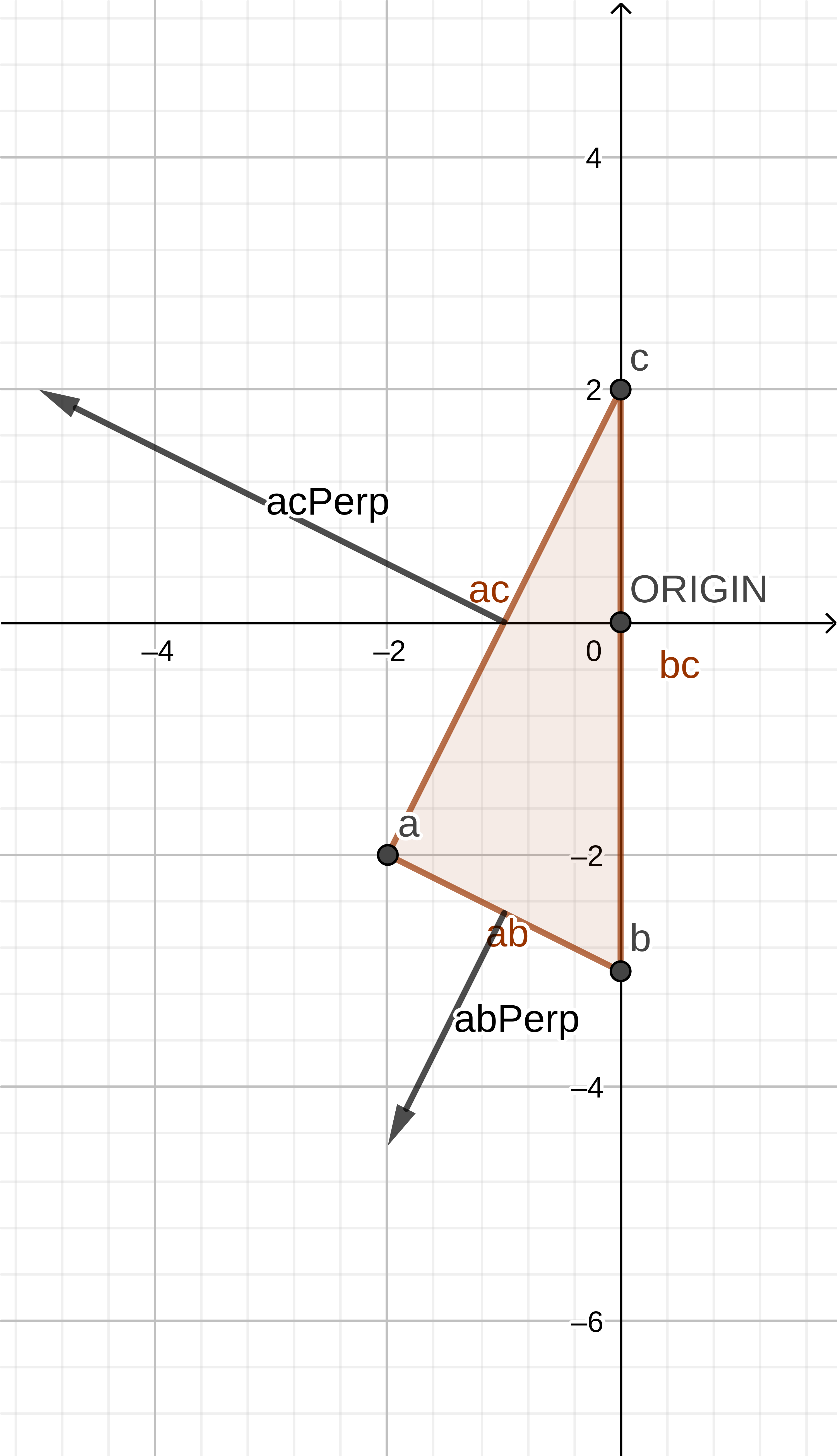
- Take the points of the simplex of the triangle.
- Since a collision has been detected, the loop is exited and
Collision
information about the collision between the two figures is returned.
direction = simplex.CalculateDirection(); } // No direction calculated, intersection detected return new Collision(a, b);
Conclusion
I hope this article helps you understand the GJK algorithm. The algorithm gives a yes / no answer about the presence of a conflict between the two figures. A working example with polygons and circles can be viewed in the repository for this post . You can expand this code with additional algorithms and techniques by trying to get the penetration distance between the two figures, the collision normal, and the contact point. The dyn4j post has links to good resources on various collision / response recognition algorithms; if you want to expand GJK, then you should study them.