Somehow I fell into the hands of a test task. Academic interest prevailed and I decided to sit on this task. My solution does not claim to be optimal and correct. I was just curious to solve it.
Initial data
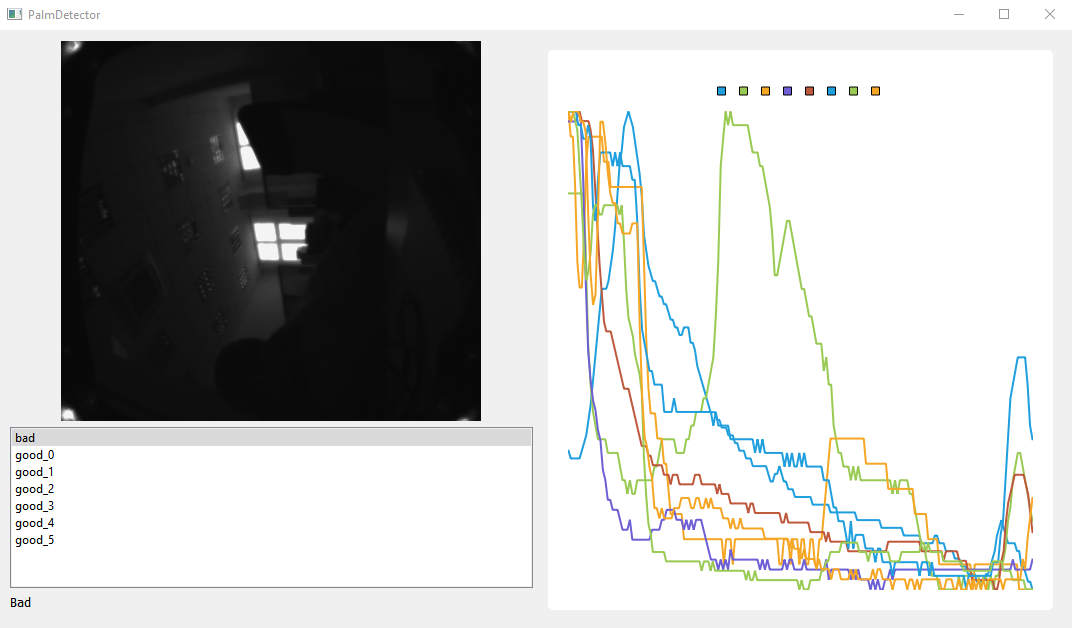
The essence of the task is to write a program that determines whether the palm is attached to the scanner by the image of images from the palm vein scanner.
Initial data - several images with a known result.

Result
The program with a graphical interface with the ability to select images from the list. After selection, the image is analyzed and after analysis, the result is displayed in the form of the inscription Good or Bad .

Algorithm
The image analysis algorithm is quite simple. To start, I created the ImageAnalyser class with the following interface
class ImageAnalyser { public: ImageAnalyser(); explicit ImageAnalyser(const QImage&); bool analyze(const QImage&); bool analyze(); std::vector<std::vector<int>> data(); virtual ~ImageAnalyser(); };
Inside this class, I decided to conditionally divide the image into 4 parts for each light source. And for each image, calculate the average brightness relative to the X and Y axes. This is clearly demonstrated in the image below.

As a result, we get eight graphs with an average brightness level.

Next, you need to analyze these graphs. I decided to use the correlation function by comparing the resulting graphs with some “perfect” graph. The ideal graph in this case is just a rectangle, which I get in the following way:
std::vector<int> ImageAnalyser::prepare_ideal_array(const std::vector<int>& array) { unsigned long min = static_cast<unsigned long>(array.size() * 0); unsigned long max = static_cast<unsigned long>(array.size() * 0.45); int ideal_value = 100; std::vector<int> ideal; ideal.resize(array.size()); for(unsigned long i = min; i < max; ++i) { ideal[i] = ideal_value; } return ideal; }
To compare the graphs and, accordingly, get the correlation value, I used the gsl_stats_correlation function, the implementation of which I honestly stole from the GNU Scientific Library .
double ImageAnalyser::gsl_stats_correlation(const std::vector<int>& data) { std::vector<int> ideal = prepare_ideal_array(data); const int stride1 = 1; const int stride2 = 1; double sum_xsq = 0.0; double sum_ysq = 0.0; double sum_cross = 0.0; double mean_x = data[0]; double mean_y = ideal[0]; for (unsigned int i = 1; i < data.size(); ++i) { double ratio = i / (i + 1.0); double delta_x = data[i * stride1] - mean_x; double delta_y = ideal[i * stride2] - mean_y; sum_xsq += delta_x * delta_x * ratio; sum_ysq += delta_y * delta_y * ratio; sum_cross += delta_x * delta_y * ratio; mean_x += delta_x / (i + 1.0); mean_y += delta_y / (i + 1.0); } double r = sum_cross / (sqrt(sum_xsq) * sqrt(sum_ysq)); return r; }
Next, you just need to analyze the correlation values. I decided that if at least one correlation value is less than 0.5, then the palm is not attached to the sensor or is poorly attached.
bool ImageAnalyser::is_good(const vector<double>& correlation, const vector<int>& maximums) { bool result = true; double min_corr = *std::min_element(correlation.begin(), correlation.end()); if (min_corr < 0.5) { result = false; } double min_val = *std::min_element(maximums.begin(), maximums.end()); if (min_val < 30) { result = false; } return result; }
It is also seen from the code that an analysis of the brightness level is performed - if the value is less than 30, then we also believe that the palm is not attached.
Stack of technologies used
- C / c ++
- Qt creator
- QtCharts
- GNU Scientific Library
Source code
https://github.com/techlinked/PalmDetector.git