
I am sure that many of the readers sometimes engaged in useless nonsense in the classroom instead of listening to the teacher. I did exactly that, and one way to kill time was to play on paper. The preview game (whose name I still do not know) seemed especially interesting to me, but there are two reasons: it does not require a second person and it can be completed! True, this was extremely rare. For a long time I was wondering how simple the solution may turn out to be, and now, after many years, it will not be difficult to find it programmatically.
rules
First, it’s worth describing the rules. The game begins with the following field:
123456789
111213141
516171819
Here, all numbers from 1 to 19 are recorded character by character, with the exception of 10. The numbers are arranged from left to right, line by line. The rules are quite simple - at each step you need to cross out 2 numbers that correspond to the following criteria:
- the numbers must be either the same or in total give 10 (1 and 1, 3 and 7, 8 and 2, etc.);
- they should either stand on top of each other, or be arranged sequentially. In this case, already crossed out numbers are ignored.
One of the options for the first few moves is shown below:
1
23456789
1
11213141
5161718
19
#2345678
9
#
1
1213141
5161718##
#2345678#
##1213141
5161718##
At the moment when there are no more moves, all the unmarked numbers are added to the end. The game ends when the entire field is crossed out.
#2345678#
##1213141
51
6
171
8
##
23
4
567
8
12
131415161
718
#2345678#
##1213
1
41
5
1
#
1
71###
23#567#12
131415
1
61
718
#2345678#
##1213#41
5###71###
2
3
#567#12
1
3
1415#61
718
...
The number of available moves is rapidly increasing, the game begins to branch strongly. Often the table becomes so long that it overflows to the next page in a notebook. It’s easier to start a new batch. Sometimes I continued out of perseverance, but in the end I gave up.
This raises the reasonable question - how fast can you finish this game? In childhood, it was possible to find a solution in one column on a notebook sheet - this is about 40 lines or 360 characters.
I don’t know the guaranteed way to complete the game. It is completely not clear how to choose a strategy. You can try playing it yourself if you haven’t.
Decision
How are solutions to such problems sought? I do not know for sure, but I chose the usual bust.
We need a queue, first consisting only of a single initial configuration. At each step, we take the next configuration from the queue, look at all the moves available from it, and either add them all to the end of the queue, or declare ourselves the winner if there are no such moves.
123456789 #23456789 12345678# 123456789 123456789 123456789 123456789 ...
111213141 #11213141 #11213141 ##1213141 1##213141 11#213141 11121314# ...
516171819 516171819 516171819 516171819 516171819 516#71819 51617181# ...
If you do not dwell on the first available solution, then this algorithm will produce all possible solutions (in the presence of an infinite amount of RAM).
In practice, such a naive approach will not help at all, at least because of the constantly appearing duplicates in the queue. Therefore, some optimizations will be required, which I will now explain:
- Naturally, configurations need to be cached so as not to re-queue them. This will greatly increase memory usage, but still will not help to get a solution in a reasonable amount of time. Moreover, the question of comparing configurations arises sharply. Since two winning configurations of the same size will always consist only of strikethrough numbers, an additional way is needed to distinguish them, otherwise not all solutions will be found;
- to make the search meaningful and fast, it is better to use a priority queue. The fewer numbers on the field (including crossed out), the earlier such a configuration should be considered;
- if you need not one solution, but many, it is better to limit the maximum number of digits per field, the search will issue solutions much earlier.
Answer
If everything is correct, it turns out that the minimum solution consists of only 68 characters or 8 lines!
I will bring it in the form of gif-animation. Some moves were glued into one to reduce the number of frames:
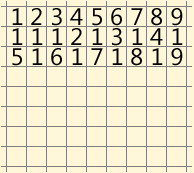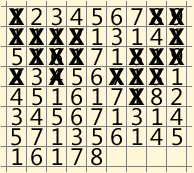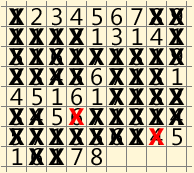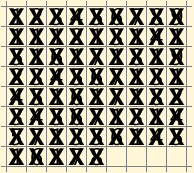
To be honest, I was struck by how short this decision is. But maybe this luck and other decisions will not be met soon and will be very long?
No, decisions are far from rare. The answers are 72, 74 and 76 long. There are 4 more fundamentally different solutions with a length of 80. In general, I managed to find 30 solutions up to 90 in length (inclusive), and if I increase the border to 100, then there will be 170 solutions. but looking for them becomes more expensive.
Under the spoiler, the optimal solution is described in detail:
123456789 111213141 516171819 123456789 111213141 5161718## 123456789 1##213141 5161718## 12345678# 1##21314# 5161718## #2345678# ###21314# 5161718## #234567## ####1314# 5161718## #234567## ####1314# 5161718## 234567131 45161718 #234567## ####1314# 51#1718## 23#567131 45161718 #234567## ####1314# 51#171### #3#567131 45161718 #234567## ####1314# 51#171### #3#567#31 451617#8 #234567## ####1314# 51#171### #3#56###1 451617#8 #234567## ####1314# 5###71### #3#56###1 451617#8 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 571356145 16178 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 57#356145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 5###56145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 #####6145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 34567131# ######145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 3456713## #######45 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 3#56713## #######45 1##78 #234567## ####1314# 5###71### #3#56###1 451617### 3#56713## #######45 1##78 #234567## ####1314# 5###71### #3#56###1 45161#### ##56713## #######45 1##78 #234567## ####1314# 5###7#### #3#56###1 45161#### ##567#3## #######45 1##78 #234567## ####1314# 5######## ###56###1 45161#### ##567#3## #######45 1##78 #234567## ####1314# ######### ####6###1 45161#### ##567#3## #######45 1##78 #234567## ####1314# ######### ####6###1 45161#### ##56##### #######45 1##78 #234567## ####1314# ######### ####6###1 45161#### ##5###### ########5 1##78 #234567## ####1314# ######### ####6###1 45161#### ######### ######### 1##78 #234567## ####131## ######### ########1 45161#### ######### ######### 1##78 #234567## ####13### ######### ######### 45161#### ######### ######### 1##78 #234567## #####3### ######### ######### 4516##### ######### ######### 1##78 #23456### ######### ######### ######### 4516##### ######### ######### 1##78 #2345#### ######### ######### ######### #516##### ######### ######### 1##78 #234##### ######### ######### ######### ##16##### ######### ######### 1##78 #23###### ######### ######### ######### ##1###### ######### ######### 1##78 #23###### ######### ######### ######### ######### ######### ######### ###78 #2####### ######### ######### ######### ######### ######### ######### ####8 ######### ######### ######### ######### ######### ######### ######### #####
My Java solution code can be viewed at this link , but I warn you that it is terrible, because originally written not for publication. In its current form, it finds all solutions up to 70 characters (that is, only one solution). This is easy to fix by playing around with the conditions in the code.
Thanks for your attention!