Clever Geek Handbook

The number underlying modern music



Why twelve?



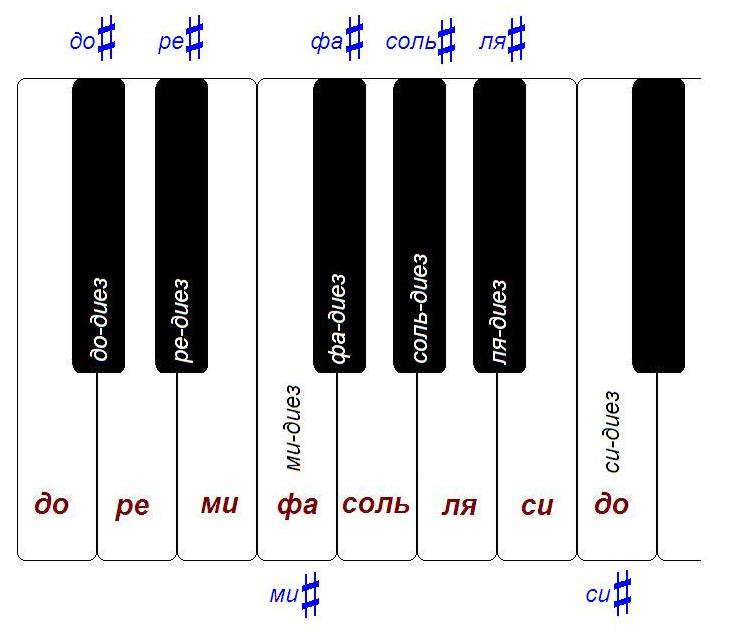
If you look at the keyboard, you will see that each octave contains 12 semitones.

In the case of the piano, this only means that between, for example, “to” the first octave and “to” the second octave, there are 11 keys. Together with one of the “do” (for example, to the second octave) we get 12 keys: do #, re, re #, mi, fa, fa #, salt, salt #, la, la #, si, do.







But why 12?







Maybe this is just an accident? Our ancestors liked the number 12, they have 12 everywhere: 12 months, 12 zodiac signs, 12 tribes of Israel, 12 apostles, ... and here they decided, let it be 12, and so it was commanded. Or is there still an objective law, and this number is not accidental?







In this article I will try to demonstrate that this is not an accident. Sufficiently general requirements, quite natural for modern (western) music, with mathematical necessity, lead us to the number 12. It is interesting that the reason why we have this value is the property of another number (see the end of the article). You can even say that it lies at the heart of modern sound.







Formulation of the problem



First, let's try to formalize the task.







We have a reference frequency $ \ omega_0 $ . We will call it tonic. We also have an octave with a frequency $ 2 \ omega_0 $ . Now we need to understand what options for intermediate frequencies from $ \ omega_0 $ before $ 2 \ omega_0 $ , such that a melody built on these notes would sound harmonious for our ears?







I am afraid that this formulation, although it reflects the essence of the question, is still, from a mathematical point of view, rather vague, and such a question cannot be answered unambiguously, if only because human hearing has a rather limited frequency resolution. And this is confirmed by the fact that at different times different tunes were used, for example, Pythagoras , clean , well-tempered , evenly tempered tunes. And they all sounded and sound, at least for certain works, quite acceptable.







What is harmony?



We must impose some additional conditions. But first we must answer one important question: what do we perceive as harmonious sound?







Let's look at two sounds - with frequencies $ \ omega_1 $ and $ \ omega_2 $ .







Take the ratio of these frequencies. This relation can be represented as a product of numbers $ a_1 ^ {k_1} \ cdot a_2 ^ {k_2} \ cdot ... \ cdot a_l ^ {k_l} $ where $ a_1, a_2, ..., a_l $ Are prime numbers, and $ k_1, k_2, ..., k_l $ - integers, for example, this ratio may equal $ 2 ^ {- 3} \ cdot3 \ cdot5 $ . And than these prime numbers ( $ a_1, a_2, ..., a_l $ ) less, the more harmonious for our ear this interval will sound (I found this statement here (see the second paragraph) )







So, for example, the most harmonious sound in accordance with this statement will be an octave (frequency change by 2 times). And the next harmonic intervals will be the fifth (frequency change in $ 3/2 $ times) and a quart (frequency change in $ 4/3 $ times).







But not so simple with this statement. So, for example, it is not very clear how the degree affects. For example, what is more harmonious multiplication by $ 3 ^ 2 $ or 7? I do not know whether this question has been studied or not, and is it possible, in principle, to give an answer to it. Also, the perception of harmony is a rather subjective thing. So, modern music is full of sounds that would have been perceived for 100-200 years only as a terrible cacophony.







The first condition. Tonic, Quart, Quint, Octave



This uncertainty is not a problem for our little research. The fact is that the only conclusion I want to draw from this statement is that in our case, in any case, there should be at least the "most harmonious" intervals, namely, an octave, a quart and a fifth. That is, along with tonic with a frequency $ \ omega_0 $ and octave with a frequency $ 2 \ omega_0 $ we must also have a fifth and a fourth, with frequencies respectively $ {3 \ over 2} \ omega_0 $ , $ {4 \ over 3} \ omega_0 $ or something very close that we could not distinguish from a pure fifth and fourth.







Note: in fact, only tonics, fifths and octaves are enough. The presence of a fifth gives us both a quart and an addition to an octave, and due to the second condition (invariance), which is described below, we must also have a quart from tonic. That is, the need for a quart is a consequence of the presence of a fifth and the requirement of invariance.







And this is our first requirement.







The second condition. Invariance



Our second requirement is invariance. And this is an important requirement of modern music. This requirement consists in the fact that all harmonies in any keys should sound the same. If we are talking about the modern system, which is used to tune the piano, then this means that a quint, consisting of seven half-tones, should sound the same, regardless of what sound it is built from. That is, the frequency ratio between do and salt should be the same as for do # - salt #, re - la, re # - la #, ... and equal $ 3/2 $ . And this invariance should apply, of course, not only to the fifth, but also to any intervals. An important advantage of this system is the ability to transpose the play to any interval. This is the essence of uniform temperament.







I must say that this requirement of invariance is not so obvious, and this approach was applied relatively recently, only in the 18th century. The systems used before (for example, Pythagoras and pure) did not possess such a property. For example, listen to the Sonata for Microtonal Piano (Ben Johnston) , written in a clean system (prime limit = 5). It feels like the piano is not tuned. All the wealth of modern harmonies is based precisely on this invariance. For example, Bach's "Well-Tempered Clavier" appeared precisely thanks to a new approach to tuning keyboards. It was this invariance that enabled Bach to create harmonic sequences that were simply impossible before.







So, now we have all the data necessary for the calculation.







Payment



Let's build a scale from a tonic to an octave that satisfies both requirements.

Suppose that in this case we get $ N $ sounds (including an octave). it $ N $ and is the desired number. We want to show that $ N $ under our conditions should be 12.







A consequence of the second requirement is that the interval between the frequencies of neighboring sounds must be the same and must be equal $ 2 ^ {1 \ over N} $ .







Now the first requirement says that there should be two sounds in our row, corresponding (with a good approximation) to the frequencies $ {3 \ over 2} \ omega_0 $ and $ {4 \ over3} \ omega_0 $ . This is the fifth and fourth. Suppose a quart is $ n_1 $ sound in our row, and the fifth - $ n_2 $ -Oh. We denote $ n = n_2 - n_1 $ .







It is easy to see that the change in frequency between a quart and a fifth (frequency ratio) is $ 9/8 $ .







But, according to our second condition, this should also be equal $ 2 ^ {n \ over N} $ .







So, we got the formula:







$ 2 ^ {n \ over N} \ approx 9/8 $







After simple transformations, we get the basic formula:







$ n \ approx N (2 \ log_2 {3} - 3) = N \ cdot $ 0.170







It is easy to see that the solution (of course, approximate) is $ N = 6i $ where $ i $ - any natural number (small enough, because nevertheless 0.170 differs from 1/6).







Let's look at a case $ i = 1 $ . In this case $ N = 6 $ , $ n = 1 $ . That is, this is a variant of the modern system, only without semitones, only with tones (do, re, mi, fa #, salt #, la #, do). But, as you can see, in this case the quart (f) and quint (salt) did not fall into this scale.







That is, the only option for us may be







$ N = 12 i $ where $ i $ - any natural number ( $ i $ small enough). Happening $ i = 1 $ just corresponds to our modern system, which is called the uniformly temperamental system.







But why not 24 or more? The reason is simple - I can assume that such a graduation is already excessive for our perception. Therefore, only one number remains: 12.







If you are not satisfied with the given train of thought, then here you can find







rigorous mathematical proof

A task:







Find the minimum positive integer N at which there is a positive integer $ n <N $ such that $ 2 ^ {n \ over N} $ differs from $ 3 \ over2 $ no more than $ \ delta $ cents .







Decision:







Denote by $ Z_n = N \ cdot (log_2 {3} -1) $ . Then, with $ \ delta <{1200 \ over N} $ (which is true for the range of those $ \ delta $ and $ N $ which we will consider) our task is to find the minimum $ N $ at which







$ {1200 \ over N} \ cdot | Z_n - round (Z_n) | <\ delta $ ,







Where $ round $ - function rounding to the nearest integer.







We will solve this problem numerically.







image







Now it's time to decide $ \ delta $ .







What is the value (in cents) of the discrepancy between the pure fifth and “our” fifth, which we consider acceptable? Many people hear, for example, that the big / small third in the evenly temperament system "fakes". But this is only about 15 cents relative to pure intervals. Therefore, our requirement should be better than 15 cents. Some sources say that at certain frequencies, musicians distinguish up to 5 - 6 cents. Therefore wise to take $ \ delta = 5 $ .







Then the table clearly shows that the smallest $ N = 12 $ . The following are satisfactory $ N = 17,24,29,34,36,41, ... $ .







Comment:

Next iteration, for each $ N $ you need to also check the sound and other intervals. When $ N = 17 $ for example, thirds become completely "fake": more than 30 cents (for a large third).







So our answer is: $ N = 12 $ . Q.E.D.







And by the way, it’s clear that our answer will not change if we instead $ \ delta = 5 $ take, for example, 10 or even 15.







Conclusion Underlying number



Surprisingly, it turns out that the number underlying the modern musical system and contemporary (European) music is $ \ log_2 {3} $ , namely, that with good accuracy (0.1%) the following equality holds:







$ \ log_2 {3} \ approx 19/12 $







More articles:


All Articles