Many tasks in the field of Computer Science, which at first glance seem new or unique, are actually rooted in classical algorithms, coding methods, and development principles. And established techniques are still the best way to solve such problems!
The book will give you the opportunity to deeper learn the Python language, test yourself on time-tested tasks, exercises and algorithms. You have to solve dozens of programming tasks: from the simplest (for example, find list items using binary sorting) to complex ones (clustering data using the k-means method). Working through examples devoted to search, clustering, graphs, etc., you will remember what you have forgotten about, and master the classical techniques for solving everyday problems.
Who is this book for?
This book is intended for middle and high level programmers. Experienced professionals who want to deepen their knowledge of Python will find here tasks that are familiar from the time they taught computer science or programming. Mid-level programmers will become familiar with these classic tasks in their chosen language - Python. For developers who are preparing for a programming interview, the publication is likely to become valuable preparatory material.
In addition to professional programmers, this book may be considered useful by students studying for undergraduate programs in computer science and interested in Python. It does not claim to be a rigorous introduction to data structures and algorithms. This is not a tutorial on data structures and algorithms. You will not find proof of theorems or the abundant use of O big notations on its pages. On the contrary, this book is positioned as an accessible practical guide to methods for solving problems that should become the end product of studying the data structure, algorithms and classes of artificial intelligence.
I emphasize again: it is assumed that readers are familiar with the syntax and semantics of Python. A reader with zero programming experience is unlikely to benefit from this book, and a programmer with zero experience in Python will probably be difficult. In other words, “Classical Computer Science Tasks in Python” is a book for Python programmers and computer science students.
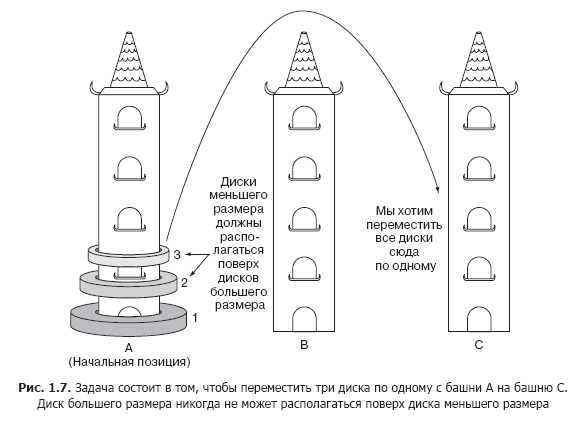
Excerpt. 1.5. Hanoi towers
There are three tall vertical columns (hereinafter - towers). We will designate them A, B and C. Disks with holes in the center are strung on tower A. The widest disk - we will call it disk 1 - is located below. The remaining disks located above it are indicated by increasing numbers and gradually taper up. For example, if we had three disks, the widest of them, the one below, would have number 1. The next widest disk, at number 2, would be located above disk 1. Finally, the narrowest disk, at number 3 would lie on disk 2.
Our goal is to move all drives from tower A to tower C, taking into account the following restrictions.
- Disks can only be moved one at a time.
- The only drive available for moving is the one located at the top of any tower.
- A wider drive can never be placed on top of a narrower one.
Schematically, the task is shown in Fig. 1.7.
1.5.1. Tower Modeling
A stack is a data structure modeled on a last-in-first-out (LIFO) principle. The last thing that gets on the stack becomes the first one that is fetched from there. The two main operations of the stack are push (put) and pop (extract). The push operation pushes a new item onto the stack, and pop removes it from the stack and returns the last item inserted. You can easily model the stack in Python using the list as a backup storage (Listing 1.20).
Listing 1.20. hanoi.py
from typing import TypeVar, Generic, List T = TypeVar('T') class Stack(Generic[T]): def __init__(self) -> None: self._container: List[T] = [] def push(self, item: T) -> None: self._container.append(item) def pop(self) -> T: return self._container.pop() def __repr__(self) -> str: return repr(self._container)
The presented Stack class implements the __repr __ () method, which makes it easy to examine the contents of the tower. __repr __ () is what will be output when the print () function is applied to the stack.
As stated in the introduction, type annotations are used in the book. Importing Generic from an input module allows Stack to be a parametric class for a specific type in type annotations. An arbitrary type T is defined in T = TypeVar ('T'). T can be any type. When the type annotation is subsequently used for Stack when solving the Hanoi tower problem, the prompt will be Stack [int], that is, the int type will be used instead of T. In other words, here the stack is a stack of integers. If you are having difficulty with type annotations, take a look at Appendix B.
Stacks are perfect for the Hanoi tower challenge. In order to move the disk to the tower, we can use the push operation. In order to move the disk from one tower to another, we can push it from the first (pop) and place it on the second (push).
Define the towers as Stack objects and fill the first one with disks (Listing 1.21).
Listing 1.21. hanoi.py (continued)
num_discs: int = 3 tower_a: Stack[int] = Stack() tower_b: Stack[int] = Stack() tower_c: Stack[int] = Stack() for i in range(1, num_discs + 1): tower_a.push(i)
1.5.2. Solving the Tower of Hanoi Problem
How can I solve the problem of Hanoi towers? Suppose we are trying to move only one drive. Then we would know how to do this, right? In fact, moving one disk is a basic case for a recursive solution to this problem. Moving multiple drives is a recursive case. The key point is that we, in fact, have two scenarios that need to be encoded: moving one disk (base case) and moving several disks (recursive case).
To understand the recursive case, consider a specific example. Suppose we have three disks - the upper, middle and lower, located on tower A, and we want to move them to tower C. (Subsequently, this will help to schematically describe the problem.) First we could move the upper disk to tower C. Then - move the middle disk to tower B, and after that the upper disk from tower C to tower B. Now we have the lower disk still located on tower A and the two upper disks on tower B. Essentially, we have already successfully moved two drive from one tower (A) to another (B). Moving the lower disk from A to C is the basic case (moving one disk). Now we can move the two upper disks from B to C using the same procedure as from A to B. We move the upper disk to A, the middle disk to C, and finally the upper disk from A to C.
In computer science classes, small models of these towers are often found, built from pins and plastic disks. You can make your own model with three pencils and three sheets of paper. Perhaps this will help you visualize the solution.
In the example with three disks, there was a simple basic case of moving one disk and a recursive case of moving the remaining disks (in this case, two) using a temporary third tower. We can break the recursive case into the following steps.
- Move the top n - 1 drives from tower A to tower B (temporary), using C as an intermediate tower.
- Move lower drive from A to C.
- Move n - 1 disks from tower B to tower C, tower A is intermediate.
Surprisingly, this recursive algorithm works not only for three, but for any number of disks. Encode it as the hanoi () function, which is responsible for moving disks from one tower to another using a third temporary tower (Listing 1.22).
Listing 1.22. hanoi.py (continued)
def hanoi(begin: Stack[int], end: Stack[int], temp: Stack[int], n: int) -> None: if n == 1: end.push(begin.pop()) else: hanoi(begin, temp, end, n — 1) hanoi(begin, end, temp, 1) hanoi(temp, end, begin, n - 1)
After calling hanoi (), you need to check towers A, B, and C to make sure that the disks have been moved successfully (Listing 1.23).
Listing 1.23. hanoi.py (continued)
if __name__ == "__main__": hanoi(tower_a, tower_c, tower_b, num_discs) print(tower_a) print(tower_b) print(tower_c)
You will find that the drives have indeed been moved. When coding the solution to the Hanoi tower problem, it is not necessary to understand every step necessary to move several disks from tower A to tower C. We came to understand the general recursive algorithm for moving any number of disks and systematized it, allowing the computer to do the rest. This is the power of formulating recursive solutions to problems: we can often imagine solutions abstractly, without wasting energy on the mental representation of each individual action.
By the way, the hanoi () function will be executed exponentially depending on the number of disks, which makes the solution to the problem even for 64 disks unsuitable. You can try to execute it with a different number of disks by changing the variable num_discs. As the number of disks increases, the number of steps to complete the Hanoi tower task grows exponentially, more details can be found in many sources. If you are interested in learning more about the mathematics behind the recursive solution of this problem, see Karl Birch’s explanation in the article “On Hanoi Towers” .
1.6. Real applications
The various methods presented in this chapter (recursion, memoization, compression, and manipulation at the bit level) are so widespread in the development of modern software that without them it is impossible to imagine the world of computing. Despite the fact that tasks can be solved without them, it is often more logical or expedient to solve them using these methods.
In particular, recursion underlies not only many algorithms, but even entire programming languages. In some functional programming languages, such as Scheme and Haskell, recursion replaces loops used in imperative languages. However, it should be remembered that everything that can be achieved using the recursive method can also be performed iteratively.
Memoization has been successfully used to speed up the work of parsers - programs that interpret languages. This is useful in all tasks where the result of a recent calculation is likely to be requested again. Another area of memoization is the runtime of programming languages. Some of these runtimes, for example, for the Prolog version, automatically save the results of function calls (auto-mash), so the function does not have to be executed the next time with the same call. This is similar to the @lru_cache () decorator in fib6 ().
Compression has made the world of the Internet, with its limited bandwidth, more bearable. The bit string method discussed in Section 1.2 is applicable to simple data types in the real world that have a limited number of possible values, for which even 1 byte is redundant. However, most compression algorithms work by searching for patterns or structures in a dataset that eliminate duplicate information. They are much more complicated than described in section 1.2.
Disposable ciphers are not suitable for general encryption cases. They require that both the encoder and the decoder have one of the keys (dummy data in our example) to restore the original data, which is too cumbersome and in most encryption schemes does not allow to achieve the goal of keeping the keys secret. But you might be interested to know that the name “one-time cipher” was invented by spies who during the Cold War used real paper notebooks with fictitious data recorded in them to create encrypted messages.
These methods are the building blocks of programs; other algorithms are based on them. In the following chapters you will see how widely they are applied.
about the author
David Kopec is a Senior Lecturer in Computer Science and Innovation at Champlain College in Burlington, Vermont. He is an experienced software developer and author of Classic Computer Science Problems in Swift (Manning, 2018) and Dart for Absolute Beginners (Apress, 2014). David earned a bachelor's degree in economics and a master's degree in computer science from Dartmouth College. You can contact him on Twitter by @davekopec.
»More details on the book can be found on the publisher’s website
» Contents
» Excerpt
25% off coupon for hawkers - Python
Upon payment of the paper version of the book, an electronic book is sent by e-mail.