Quasi-Newton methods, or when there are too many second derivatives for Athos
When you first get acquainted with quasi-Newtonian methods, you may be surprised twice. First, after a quick glance at the formulas, doubts arise that this can work at all. However, they work. Further it seems doubtful that they will work well. And it’s all the more surprising to see how much faster they are than the various variations of gradient descent, not on specially constructed tasks, but on real ones taken from practice. And if after this there are still doubts mixed with interest, then you need to understand why this something works at all.
The origin and basic ideas that drive gradient methods, including the Newton method, have already been considered . Namely, we relied on the information about the behavior of the function in the vicinity of the current position, which gives us a simple mathematical analysis. At a minimum, it was assumed that information on the first derivatives was available to us. What if this is all that is available to us? Is gradient descent our sentence? Of course, yes, unless you suddenly remember that we are dealing with a process in which the objective function is properly processed. And if so, why don't we use the accumulated information about the behavior of the function in order to make our walk on its surface a little less blind?
The idea of using information about the path covered lies at the heart of most ways to speed up the descent methods. This article discusses one of the most effective, although not the cheapest, way of accounting for this kind of information, leading to the idea of quasi-Newtonian methods.
In order to understand where the legs of quasi-Newtonian methods grow and where the name comes from, we will again have to return to the minimization method based on the direct solution of the stationary point equation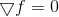
. Just as the consideration of the Newton method applied to the solution of this equation led us to the optimization method of the same name (which, unlike its progenitor, has a global region of convergence), we can expect that consideration of other methods for solving systems of nonlinear equations will be fruitful in plan ideas for building other optimization methods.
Let me remind you that Newton’s method for solving the system of equations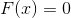
, is based on the replacement in the neighborhood of some point close to the solution 
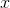the functions 
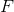its linear approximation 
where 
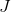Is a linear operator, which, when 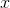is a vector and 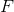has partial derivatives with respect to each variable, coincides with the Jacobi matrix 
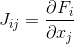. Next, the equation is solved 
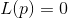and point 
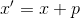taken as a new approximation to the desired solution. It is simple and it works.
But what if we for some reason cannot calculate the Jacobi matrix? The first thing that comes to mind in this case is that if we cannot calculate the partial derivatives analytically, then we can well get a numerical approximation for them. The simplest (although by no means the only) variant of such an approximation can be the formula of right finite differences: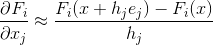
where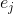 
Is the jth base vector. The matrix composed of such approximations will be denoted 
. An analysis of how much replacement 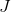on in Newton's method, its convergence affects, a fairly large number of works are devoted, but in this case we are interested in another aspect. Namely, such an approximation requires the calculation of the function at N additional points, and, in addition, the function 
at these points the function interpolates 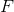, i.e.
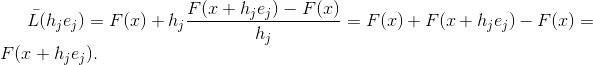
Not every approximation of the Jacobi matrix has this property, but every matrix of an affine function with this property is an approximation of the Jacobi matrix. Indeed, if
and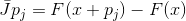 
then at 
. This property, namely, the interpolation property, gives us a constructive way to generalize the Newton method.
Let be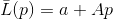
- function satisfying the requirement 
for some system of linearly independent vectors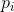 
. Then such a function is called a secant function 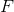, and the equation that defines it is the secant equation . If the system of vectors is complete (that is, there are exactly N of them and they are still linearly independent), and, in addition, the system of vectors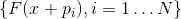 
linearly independent then 
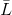defined uniquely.
Any method based on local change of equation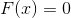 equation of the form 
where 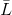satisfies the secant equation , called the secant method .
A fair question arises about how to construct the secant for a function in the most rational way.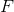 . The following line of reasoning seems obvious: let an affine model be constructed at the point x that interpolates the given function at the points 
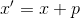. Equation solution gives us a new point . Then to build an affine model at a point 
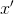it is most reasonable to choose interpolation points so that the value 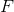already known - that is, take them from the set 
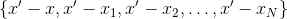. There are different options for which points to choose from the many previously used. For example, you can take as interpolation points those in which 
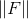matters least or just the first 
points. In any case, it seems obvious that 
should be included in many interpolation points for the new affine model. So beyond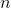 
steps of the iterative process in our set can be up to 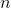displacements built on previously passed points. If the process is constructed in such a way that the new affine model uses no more 
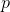of the previous values, then such a process is called the p-point secant method.
At first glance, it might seem that the N-point secant method is the best candidate for the role of replacing the Newton method, since it makes maximum use of the information that we obtain in the process of solving, and at the same time minimizes the number of additional calculations - we use the value of the function in the latter N points passed. Unfortunately, it is not. The thing is that the vector system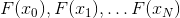
stubbornly refuses to be linearly independent with a sufficiently large N. In addition, even if this condition turns out to be fulfilled and the corresponding affine model still exists, then there’s a chance that the directions 
also prove to be linearly independent, it turns out even less. And this entails the fact that the affine model, although it exists, is degenerate and practically unsuitable.
In general, the most stable is the 2-point secant method. That is, a method in which at each iteration we have to calculate additional N-1 values of the function. This is clearly not suitable for our practical purposes.
Then the question is - what was all this?
The way out is simple, although not obvious. If we do not have the technical ability, based on the already calculated values, to uniquely determine an affine model that satisfies the secant equation, then it is not necessary. We take the equation of secants as a basis, but we will require that it be satisfied only for some incomplete system of vectors
. In other words, we will require that the interpolation condition is satisfied only for a sufficiently small number of known values. Of course, in this case we can no longer guarantee that the matrix used in such a model will tend to the Jacobi matrix, but we will not need this. Adding to this, the affine model must interpolate the function at the current point, i.e. 
, we get the following formulation of the secant method:
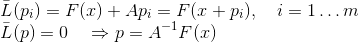
Bruiden was the first to consider methods of this kind for m = 1, calling them quasi-Newtonian. It is clear that the secant condition in this case allows us to uniquely identify the matrix
only if additional conditions are imposed on it, and each such additional condition gives rise to a separate method. Bruyden himself reasoned as follows:
as the movement in the direction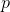 from point 
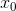to the point 
does not give us any additional information on how the function changes in other than 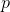directions, then the effect of the new affine function on the vector 
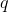should differ from the effect of the old function on the same vector the less the more different 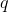from 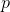. As a last resort, when 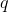orthogonal 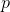, the behavior of the new function should not be different from the behavior of the old one.
Breiden's idea is brilliant in its simplicity. Indeed, if we do not have new information about the behavior of the function, then the best we can do is try not to foul the old one. Then the additional condition
for all 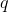such that 
allows you to uniquely determine the matrix of the new transformation - it is obtained by adding a rank 1 correction to the old matrix.
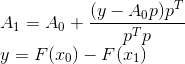
However, despite the simplicity and consistency of the conclusions made by Bruiden, they do not provide the point of support that could serve as the basis for constructing other similar methods. Fortunately, there is a more formal expression of his idea. Namely, the matrix constructed in this way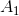
It turns out to be the solution to the following problem:
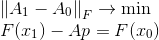
The task constraint is nothing but the secant equation, and the minimization condition reflects our desire to save as much information as possible in the matrix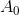
. The measure of the discrepancy between the matrices in this case is the Frobenius norm, in which the problem posed has a unique solution. This formulation may well serve as a starting point for constructing other methods. Namely, we can change both the measure by which we evaluate the introduced changes and tighten the conditions imposed on the matrix. In general, one can already work with such a formulation of the method.
Having understood the main idea, we can finally return to optimization problems and notice that the application of the Bruiden formula for recalculation of the affine model does not fall too well on our task. In fact, the first derivative of the gradient function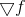
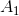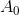there is nothing else but the Hessian matrix, which by construction is symmetric. At the same time, updating according to the Bruyden rule leads to an asymmetric matrix even was symmetrical. This does not mean that the Broyden method cannot be applied to solve the stationary point equation, but based on such an update rule, we are unlikely to be able to construct good optimization methods. In general, it is quite obvious that the quasi-Newton method should work the better, the more accurately the system of conditions of the problem describes the specifics of a specific Jacobi matrix.
To correct this drawback, we add an additional restriction to the Bruden minimization problem, explicitly requiring that the new matrix be symmetric along with the old one:
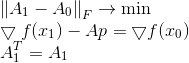
The solution to this problem is
Here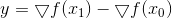
, and the matrix recalculation formula is named after its creators - Powell, Shanno and Bruyden (PSB). The resulting matrix is symmetric, but clearly not positive definite, if only suddenly 
will not be collinear 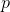. And we saw that positive certainty is highly desirable in optimization methods.
Again, we will correct the condition of the problem, using this time the scaled Frobenius norm as a measure of matrix divergence.
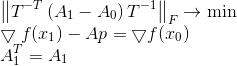
The origin of this formulation of the question is a separate big topic, but it is interesting that if the matrix T is such that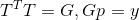
(that is, G is also an affine transformation matrix satisfying the secant equation for the direction p), then the solution to this problem turns out to be independent of the choice of T and leads to the update formula
known as the Davidon-Fletcher-Powell formula. This update method has proven itself in practice, as it has the following property:
if
and 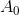positive definite then 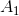also positively identified.
I note after that if the first condition is not satisfied, then there does not exist an affine function with a positive definite matrix that satisfies the secant equation.
If in the problem leading to the DFP method, we take, as a measure of the discrepancy of affine models, the distance not between the matrices themselves, but between the matrices inverse to them, we obtain a problem of the form
Its solution is a well-known formula, discovered almost simultaneously by Breuden, Fletcher, Goldfarb and Shanno (BFGS).
To date, it is believed that recalculation according to this formula is the most efficient from a computational point of view and at the same time is less prone to degeneration of the matrix with a large number of iterations. Under the same conditions as DFP, this formula preserves the property of positive definiteness.
All the described methods for updating the matrix require a correction of rank 2. This makes it easy and easy to invert the matrix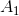 using the Sherman-Morrison formula and the value 
.
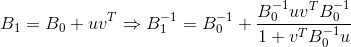
provided that the denominator of the formula is nonzero. I will not give specific formulas for updating the inverse matrices of the listed methods, since they are easy to find or derive independently. The only thing that should be noted in this case is that the variants of the methods with updating the inverse matrix are usually much less stable (that is, they suffer more from rounding errors) than those that suggest updating the original matrix. It is most effective to update not the matrix itself, but its Cholesky decomposition (unless, of course, such a decomposition takes place), since such an implementation option is more numerically stable and, in addition, minimizes the cost of solving an equation that determines the direction of motion.
It remains to consider the question of how the very first matrix should look in the quasi-Newtonian process. Everything is obvious here - the closer it is to the Hessian matrix or to its corrected version, if the Hessian does not suddenly turn out to be positive definite, the better it will be in terms of convergence. However, in principle, any positive definite matrix can be suitable for us. The simplest version of such a matrix is a single one, and then the first iteration coincides with the iteration of the gradient descent. Fletcher and Powell showed (naturally, for the DFP method) that if the quadratic function is minimized, regardless of which (positive definite) matrix is used as the initial DFP iteration, they will lead to a solution in exactly N iterations, where N is dimension of the problem, and the quasi-Newtonian matrix coincides with the Hessian matrix at the minimum point. In the general non-linear case of such happiness, we, of course, will not wait, but this at least gives reason to not worry too much about the poor choice of the initial matrix.
The described approach to the construction of quasi-Newtonian methods is not the only possible one. At a minimum, the discoverers of the described quasi-Newtonian methods and many subsequent researchers came to the same formulas on the basis of completely different considerations. However, it is interesting that as soon as a certain quasi-Newtonian method appeared, then regardless of the method of obtaining it, after a rather short time it became clear that it was a solution to some very easily interpreted optimization problem. In my opinion, it is remarkable that it is possible to bring some common denominator for such diverse methods, since this provides the basis for constructing other methods that better take into account the specifics of a particular task. In particular, there are quasi-Newtonian methods designed to update sparse matrices, methods in which as few elements as possible are subjected to change, and many others would be fantasy.
It should also be noted that methods of variable metrics, in spite of their name, do not always lead to the construction of matrices, which are actually metrics, although they do it every time it is possible at all. This is usually not a big problem, but those who want to protect themselves from a possible embarrassment may well resort to the same tricks that were made to overcome a similar problem with the Newton method - for example, by changing the direction or applying the Levenberg-Marquardt scheme . True, in this case, questions of choosing the form of a trusting region will again become relevant, but here it is necessary to choose the lesser of evils. Another solution to the problem is to use linear search methods to ensure that the necessary conditions for maintaining positive certainty are met. Wolfe’s rule guarantees the fulfillment of this condition, while the Armijo and Goldstein rules do not.
Theoretically, it is almost impossible to determine which of the huge number of possible quasi-Newtonian methods will be the most effective in relation to a certain class of problems. Usually, when formulating a method, they are limited to showing its effectiveness in minimizing a quadratic function (by the way, a method is considered effective if it leads to an exact solution in N iterations, that is, no more slowly than direct methods for solving SLAEs). In more rare cases, one can find studies of the convergence order of the method (which is usually superlinear, that is, significantly better than what gradient descent gives us), stability, and other characteristics of interest. But in general, the only reasonable criterion that allows us to judge the effectiveness of a particular method for a particular class of tasks is practice. So shovels in hand - and success in application.
The origin and basic ideas that drive gradient methods, including the Newton method, have already been considered . Namely, we relied on the information about the behavior of the function in the vicinity of the current position, which gives us a simple mathematical analysis. At a minimum, it was assumed that information on the first derivatives was available to us. What if this is all that is available to us? Is gradient descent our sentence? Of course, yes, unless you suddenly remember that we are dealing with a process in which the objective function is properly processed. And if so, why don't we use the accumulated information about the behavior of the function in order to make our walk on its surface a little less blind?
The idea of using information about the path covered lies at the heart of most ways to speed up the descent methods. This article discusses one of the most effective, although not the cheapest, way of accounting for this kind of information, leading to the idea of quasi-Newtonian methods.
In order to understand where the legs of quasi-Newtonian methods grow and where the name comes from, we will again have to return to the minimization method based on the direct solution of the stationary point equation
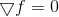. Just as the consideration of the Newton method applied to the solution of this equation led us to the optimization method of the same name (which, unlike its progenitor, has a global region of convergence), we can expect that consideration of other methods for solving systems of nonlinear equations will be fruitful in plan ideas for building other optimization methods.
Secant methods
Let me remind you that Newton’s method for solving the system of equations
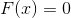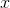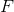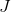, is based on the replacement in the neighborhood of some point close to the solution the functions its linear approximation where Is a linear operator, which, when 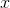is a vector and 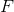has partial derivatives with respect to each variable, coincides with the Jacobi matrix 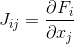. Next, the equation is solved 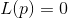and point 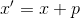taken as a new approximation to the desired solution. It is simple and it works.
But what if we for some reason cannot calculate the Jacobi matrix? The first thing that comes to mind in this case is that if we cannot calculate the partial derivatives analytically, then we can well get a numerical approximation for them. The simplest (although by no means the only) variant of such an approximation can be the formula of right finite differences:
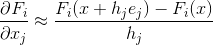where 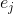Is the jth base vector. The matrix composed of such approximations will be denoted . An analysis of how much replacement 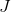on in Newton's method, its convergence affects, a fairly large number of works are devoted, but in this case we are interested in another aspect. Namely, such an approximation requires the calculation of the function at N additional points, and, in addition, the function at these points the function interpolates 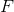, i.e.
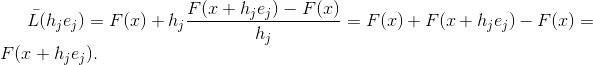
Not every approximation of the Jacobi matrix has this property, but every matrix of an affine function with this property is an approximation of the Jacobi matrix. Indeed, if
and 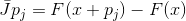then at . This property, namely, the interpolation property, gives us a constructive way to generalize the Newton method.
Let be
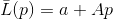- function satisfying the requirement for some system of linearly independent vectors 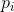. Then such a function is called a secant function 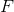, and the equation that defines it is the secant equation . If the system of vectors 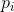is complete (that is, there are exactly N of them and they are still linearly independent), and, in addition, the system of vectors 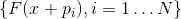linearly independent then 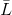defined uniquely.
Any method based on local change of equation
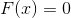equation of the form where 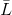satisfies the secant equation , called the secant method .
A fair question arises about how to construct the secant for a function in the most rational way.
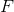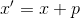. The following line of reasoning seems obvious: let an affine model be constructed at the point x that interpolates the given function at the points . Equation solution gives us a new point . Then to build an affine model at a point 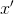it is most reasonable to choose interpolation points so that the value 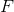already known - that is, take them from the set 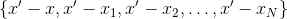. There are different options for which points to choose from the many previously used. For example, you can take as interpolation points those in which 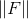matters least or just the first points. In any case, it seems obvious that should be included in many interpolation points for the new affine model. So beyond 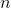steps of the iterative process in our set can be up to 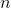displacements built on previously passed points. If the process is constructed in such a way that the new affine model uses no more 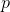of the previous values, then such a process is called the p-point secant method.
At first glance, it might seem that the N-point secant method is the best candidate for the role of replacing the Newton method, since it makes maximum use of the information that we obtain in the process of solving, and at the same time minimizes the number of additional calculations - we use the value of the function in the latter N points passed. Unfortunately, it is not. The thing is that the vector system
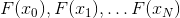stubbornly refuses to be linearly independent with a sufficiently large N. In addition, even if this condition turns out to be fulfilled and the corresponding affine model still exists, then there’s a chance that the directions also prove to be linearly independent, it turns out even less. And this entails the fact that the affine model, although it exists, is degenerate and practically unsuitable.
In general, the most stable is the 2-point secant method. That is, a method in which at each iteration we have to calculate additional N-1 values of the function. This is clearly not suitable for our practical purposes.
Then the question is - what was all this?
Quasi-Newtonian methods for solving equations
The way out is simple, although not obvious. If we do not have the technical ability, based on the already calculated values, to uniquely determine an affine model that satisfies the secant equation, then it is not necessary. We take the equation of secants as a basis, but we will require that it be satisfied only for some incomplete system of vectors
. In other words, we will require that the interpolation condition is satisfied only for a sufficiently small number of known values. Of course, in this case we can no longer guarantee that the matrix used in such a model will tend to the Jacobi matrix, but we will not need this. Adding to this, the affine model must interpolate the function at the current point, i.e. , we get the following formulation of the secant method:
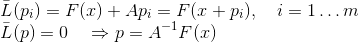
Bruiden was the first to consider methods of this kind for m = 1, calling them quasi-Newtonian. It is clear that the secant condition in this case allows us to uniquely identify the matrix
only if additional conditions are imposed on it, and each such additional condition gives rise to a separate method. Bruyden himself reasoned as follows:
as the movement in the direction
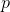from point 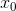to the point does not give us any additional information on how the function changes in other than 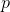directions, then the effect of the new affine function on the vector 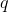should differ from the effect of the old function on the same vector the less the more different 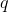from 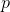. As a last resort, when 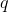orthogonal 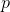, the behavior of the new function should not be different from the behavior of the old one.
Breiden's idea is brilliant in its simplicity. Indeed, if we do not have new information about the behavior of the function, then the best we can do is try not to foul the old one. Then the additional condition
for all 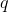such that
allows you to uniquely determine the matrix of the new transformation - it is obtained by adding a rank 1 correction to the old matrix.
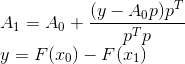
However, despite the simplicity and consistency of the conclusions made by Bruiden, they do not provide the point of support that could serve as the basis for constructing other similar methods. Fortunately, there is a more formal expression of his idea. Namely, the matrix constructed in this way
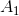It turns out to be the solution to the following problem:
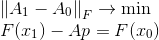
The task constraint is nothing but the secant equation, and the minimization condition reflects our desire to save as much information as possible in the matrix
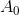. The measure of the discrepancy between the matrices in this case is the Frobenius norm, in which the problem posed has a unique solution. This formulation may well serve as a starting point for constructing other methods. Namely, we can change both the measure by which we evaluate the introduced changes and tighten the conditions imposed on the matrix. In general, one can already work with such a formulation of the method.
Quasi-Newton Optimization Methods
Having understood the main idea, we can finally return to optimization problems and notice that the application of the Bruiden formula for recalculation of the affine model does not fall too well on our task. In fact, the first derivative of the gradient function
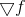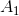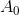there is nothing else but the Hessian matrix, which by construction is symmetric. At the same time, updating according to the Bruyden rule leads to an asymmetric matrix even was symmetrical. This does not mean that the Broyden method cannot be applied to solve the stationary point equation, but based on such an update rule, we are unlikely to be able to construct good optimization methods. In general, it is quite obvious that the quasi-Newton method should work the better, the more accurately the system of conditions of the problem describes the specifics of a specific Jacobi matrix.
To correct this drawback, we add an additional restriction to the Bruden minimization problem, explicitly requiring that the new matrix be symmetric along with the old one:
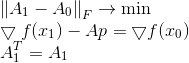
The solution to this problem is
Here
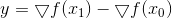, and the matrix recalculation formula is named after its creators - Powell, Shanno and Bruyden (PSB). The resulting matrix is symmetric, but clearly not positive definite, if only suddenly will not be collinear 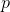. And we saw that positive certainty is highly desirable in optimization methods.
Again, we will correct the condition of the problem, using this time the scaled Frobenius norm as a measure of matrix divergence.
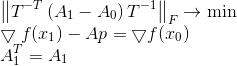
The origin of this formulation of the question is a separate big topic, but it is interesting that if the matrix T is such that
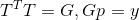(that is, G is also an affine transformation matrix satisfying the secant equation for the direction p), then the solution to this problem turns out to be independent of the choice of T and leads to the update formula
known as the Davidon-Fletcher-Powell formula. This update method has proven itself in practice, as it has the following property:
if
and 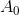positive definite then 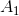also positively identified.
I note after that if the first condition is not satisfied, then there does not exist an affine function with a positive definite matrix that satisfies the secant equation.
If in the problem leading to the DFP method, we take, as a measure of the discrepancy of affine models, the distance not between the matrices themselves, but between the matrices inverse to them, we obtain a problem of the form
Its solution is a well-known formula, discovered almost simultaneously by Breuden, Fletcher, Goldfarb and Shanno (BFGS).
To date, it is believed that recalculation according to this formula is the most efficient from a computational point of view and at the same time is less prone to degeneration of the matrix with a large number of iterations. Under the same conditions as DFP, this formula preserves the property of positive definiteness.
All the described methods for updating the matrix require a correction of rank 2. This makes it easy and easy to invert the matrix
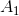using the Sherman-Morrison formula and the value .
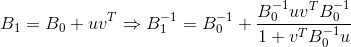
provided that the denominator of the formula is nonzero. I will not give specific formulas for updating the inverse matrices of the listed methods, since they are easy to find or derive independently. The only thing that should be noted in this case is that the variants of the methods with updating the inverse matrix are usually much less stable (that is, they suffer more from rounding errors) than those that suggest updating the original matrix. It is most effective to update not the matrix itself, but its Cholesky decomposition (unless, of course, such a decomposition takes place), since such an implementation option is more numerically stable and, in addition, minimizes the cost of solving an equation that determines the direction of motion.
It remains to consider the question of how the very first matrix should look in the quasi-Newtonian process. Everything is obvious here - the closer it is to the Hessian matrix or to its corrected version, if the Hessian does not suddenly turn out to be positive definite, the better it will be in terms of convergence. However, in principle, any positive definite matrix can be suitable for us. The simplest version of such a matrix is a single one, and then the first iteration coincides with the iteration of the gradient descent. Fletcher and Powell showed (naturally, for the DFP method) that if the quadratic function is minimized, regardless of which (positive definite) matrix is used as the initial DFP iteration, they will lead to a solution in exactly N iterations, where N is dimension of the problem, and the quasi-Newtonian matrix coincides with the Hessian matrix at the minimum point. In the general non-linear case of such happiness, we, of course, will not wait, but this at least gives reason to not worry too much about the poor choice of the initial matrix.
Conclusion
The described approach to the construction of quasi-Newtonian methods is not the only possible one. At a minimum, the discoverers of the described quasi-Newtonian methods and many subsequent researchers came to the same formulas on the basis of completely different considerations. However, it is interesting that as soon as a certain quasi-Newtonian method appeared, then regardless of the method of obtaining it, after a rather short time it became clear that it was a solution to some very easily interpreted optimization problem. In my opinion, it is remarkable that it is possible to bring some common denominator for such diverse methods, since this provides the basis for constructing other methods that better take into account the specifics of a particular task. In particular, there are quasi-Newtonian methods designed to update sparse matrices, methods in which as few elements as possible are subjected to change, and many others would be fantasy.
It should also be noted that methods of variable metrics, in spite of their name, do not always lead to the construction of matrices, which are actually metrics, although they do it every time it is possible at all. This is usually not a big problem, but those who want to protect themselves from a possible embarrassment may well resort to the same tricks that were made to overcome a similar problem with the Newton method - for example, by changing the direction or applying the Levenberg-Marquardt scheme . True, in this case, questions of choosing the form of a trusting region will again become relevant, but here it is necessary to choose the lesser of evils. Another solution to the problem is to use linear search methods to ensure that the necessary conditions for maintaining positive certainty are met. Wolfe’s rule guarantees the fulfillment of this condition, while the Armijo and Goldstein rules do not.
Theoretically, it is almost impossible to determine which of the huge number of possible quasi-Newtonian methods will be the most effective in relation to a certain class of problems. Usually, when formulating a method, they are limited to showing its effectiveness in minimizing a quadratic function (by the way, a method is considered effective if it leads to an exact solution in N iterations, that is, no more slowly than direct methods for solving SLAEs). In more rare cases, one can find studies of the convergence order of the method (which is usually superlinear, that is, significantly better than what gradient descent gives us), stability, and other characteristics of interest. But in general, the only reasonable criterion that allows us to judge the effectiveness of a particular method for a particular class of tasks is practice. So shovels in hand - and success in application.
All Articles