The generator of simple arithmetic examples for dummies and not only
Hello!
In this "article", or rather the essay, I will show a very simple way to have fun knowing the very basics of latex and python.
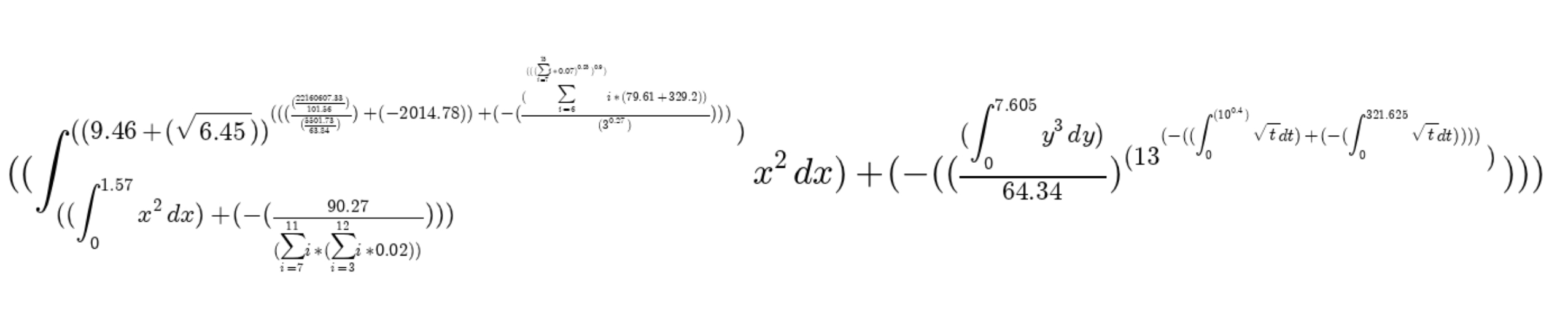
Well, you can generate simple expressions for kids to count. Or just like that. Yes, at least put on the wallpaper, if you are as fanatic as I am.
The idea is really very simple, absolutely anyone can write such a program. We want to generate an expression equal to some number n (which the user enters). Any number can be replaced with an arithmetic expression, for example, 3 = 1 + 2. And 2 is 4 / 2. This is how we generated 3 = 1 + 4/2. Similarly, we will introduce several different operations and wrap this in LaTeX, the formula language.
We need to parse the expression so that we can get the numbers out of there. Let's call our class as a generator of problems (we all miss it so much!)
The meaning of the extract_nums function is to get n pairs of numbers (a, b), where a is the position of the first character, b is the position of the last + 1.
For example, if we run the following code:
We will see:
That is, it is a tuple array. (0, 2) means that there is a number between 0 (inclusive) and 2 (not inclusive).
Now we would like to make different operators, let's start with multiplication and sum. Declare three functions
The essence of the unmin function is not only to simply convert all arguments to strings, but also to bracket one of the operands if it is less than zero. For example, we got the numbers a = 3, b = -4. If we write
Then a = "3", b = "(- 4)"
Well, the rest of the functions are clear: __c_sum returns a string of the form “13 + 4”, and __c_mul “13 * 4”.
It remains to combine these two pieces and replace each number in the expression with the expression.
Add the following code to ProblemGenerator:
complexify takes some number, and returns a string - a complicated expression. For example, if we write:
We get:
How does __rxp__ work? We randomly select the position of a number from an expression (for example, if there is an expression “13 + 35/45”, then let's say we selected (3, 5)) and replace this number with an expression equal to that number. That is, I would like to:
"13 + 35/45" - a random number (3, 5)
"13+" + "(12 + 23)" + "/ 45"
"13+ (12 + 23) / 45"
That's how __rxp__ works
Well, randexpr works quite simply. For example, if we have four steps, then the expression will open like this:
Let's try to run:
Result:
Oddly enough, the simplest remains. We will announce a number of different LaTeX operators:
Add all the functions to gen:
Finally, add the output of the result:
That's all.
In this "article", or rather the essay, I will show a very simple way to have fun knowing the very basics of latex and python.
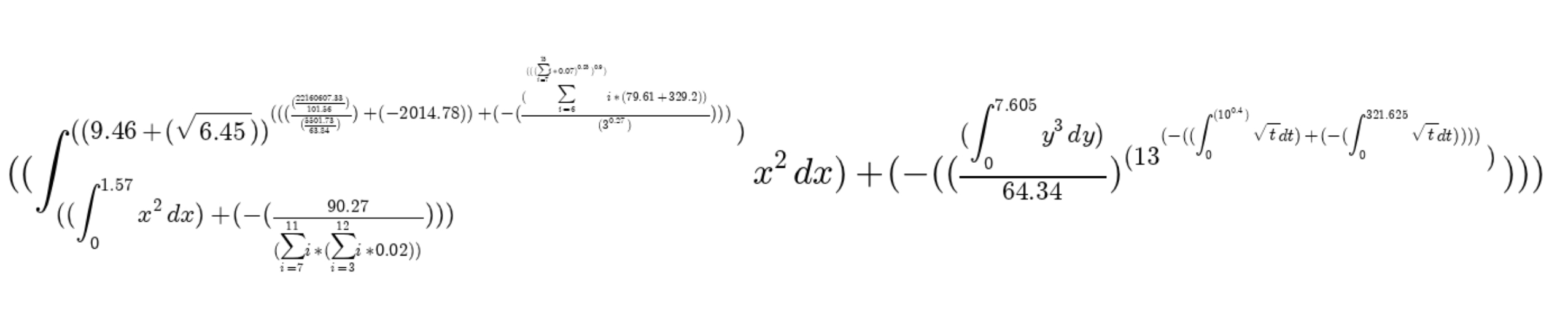
What for?
Well, you can generate simple expressions for kids to count. Or just like that. Yes, at least put on the wallpaper, if you are as fanatic as I am.
How is this supposed to work?
The idea is really very simple, absolutely anyone can write such a program. We want to generate an expression equal to some number n (which the user enters). Any number can be replaced with an arithmetic expression, for example, 3 = 1 + 2. And 2 is 4 / 2. This is how we generated 3 = 1 + 4/2. Similarly, we will introduce several different operations and wrap this in LaTeX, the formula language.
You will need...
One week experience in python and matplotlib. I'm serious.
Main mechanism
We need to parse the expression so that we can get the numbers out of there. Let's call our class as a generator of problems (we all miss it so much!)
import random from math import log import math import sys sys.setrecursionlimit(1000) # class ProblemGenerator: def extract_nums(self, exp): symbols = list(exp) NUM = "1234567890." for i in range(len(symbols)): symbols[i] = "N" if symbols[i] in NUM else "T" begins = [] ends = [] for i in range(len(symbols) - 1): fn = symbols[i] + symbols[i + 1] if fn == "TN": begins.append(i) elif fn == "NT": ends.append(i) if exp[-1] in NUM: ends.append(len(exp) - 1) if exp[0] in NUM: begins = [-1] + begins return [(x + 1, y + 1) for x, y in zip(begins, ends)]
The meaning of the extract_nums function is to get n pairs of numbers (a, b), where a is the position of the first character, b is the position of the last + 1.
For example, if we run the following code:
gen = ProblemGenerator() print(gen.extract_nums("13+256/355+25"))
We will see:
[(0, 2), (3, 6), (7, 10), (11, 13)]
That is, it is a tuple array. (0, 2) means that there is a number between 0 (inclusive) and 2 (not inclusive).
Now we would like to make different operators, let's start with multiplication and sum. Declare three functions
def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b) return a + " * " + b
The essence of the unmin function is not only to simply convert all arguments to strings, but also to bracket one of the operands if it is less than zero. For example, we got the numbers a = 3, b = -4. If we write
a = 3 b = -4 a, b = unmin(a, b)
Then a = "3", b = "(- 4)"
Well, the rest of the functions are clear: __c_sum returns a string of the form “13 + 4”, and __c_mul “13 * 4”.
It remains to combine these two pieces and replace each number in the expression with the expression.
Add the following code to ProblemGenerator:
class ProblemGenerator: ... def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e
complexify takes some number, and returns a string - a complicated expression. For example, if we write:
gen = ProblemGenerator() gen.add_expander(__c_sum) print(gen.complexify(13))
We get:
31.2 + (-18.2)
How does __rxp__ work? We randomly select the position of a number from an expression (for example, if there is an expression “13 + 35/45”, then let's say we selected (3, 5)) and replace this number with an expression equal to that number. That is, I would like to:
"13 + 35/45" - a random number (3, 5)
"13+" + "(12 + 23)" + "/ 45"
"13+ (12 + 23) / 45"
That's how __rxp__ works
Well, randexpr works quite simply. For example, if we have four steps, then the expression will open like this:
13 (5.62 + 7.38) ((20.63 + (-15.01)) + 7.38) ((20.63 + (-(67.5 + (-52.49)))) + 7.38) ((20.63 + (-((15.16 + 52.34) + (-52.49)))) + 7.38)
Let's try to run:
gen = ProblemGenerator() gen.add_expander(__c_sum) gen.add_expander(__c_mul) exp = gen.randexpr(1, 5) print(exp)
Result:
((6.63 + (56.62 + 16.8)) + (-((60.53 + 3.61) + 14.91)))
LaTeX
Oddly enough, the simplest remains. We will announce a number of different LaTeX operators:
def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c
Add all the functions to gen:
gen = ProblemGenerator() gen.add_expander(__l_sum) # gen.add_expander(__l_div) # gen.add_expander(__l_pow) # gen.add_expander(__l_sqrt) # gen.add_expander(__l_int) # gen.add_expander(__l_sig) #
Finally, add the output of the result:
import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30) # 30 . 1 plt.text(0.5, 0.5, "$" + latex_expression + "$", horizontalalignment='center', verticalalignment='center', fontsize=20) plt.show()
That's all.
Whole code
import random from math import log import math import sys sys.setrecursionlimit(1000) class ProblemGenerator: def extract_nums(self, exp): symbols = list(exp) NUM = "1234567890." for i in range(len(symbols)): symbols[i] = "N" if symbols[i] in NUM else "T" begins = [] ends = [] for i in range(len(symbols) - 1): fn = symbols[i] + symbols[i + 1] if fn == "TN": begins.append(i) elif fn == "NT": ends.append(i) if exp[-1] in NUM: ends.append(len(exp) - 1) if exp[0] in NUM: begins = [-1] + begins return [(x + 1, y + 1) for x, y in zip(begins, ends)] def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b, acc=5) return a + " * " + b def __c_sub(num): a = num + 100 ** (random.random() * 2) b = (a - num) a, b = unmin(a, b) return a + " - " + b def __c_log(num): fr = random.randint(300, 500) a = math.e ** (num / fr) a, fr = unmin(a, fr, acc=5) return "log(" + a + ") * " + fr def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c gen = ProblemGenerator() gen.add_expander(__l_sum) gen.add_expander(__l_div) gen.add_expander(__l_pow) gen.add_expander(__l_sqrt) gen.add_expander(__l_int) gen.add_expander(__l_sig) import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30) # 30 . 1 plt.text(0.5, 0.5, "$" + latex_expression + "$", horizontalalignment='center', verticalalignment='center', fontsize=15) plt.show()
Result (3 screenshots) 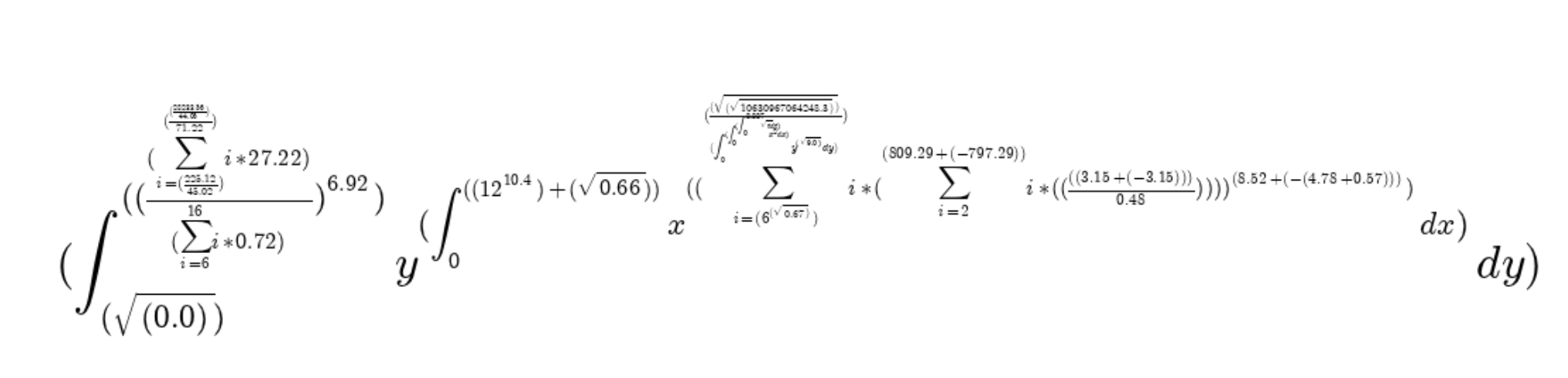





All Articles