Back to the Future? Quantum Deferred Eraser
Articles and comments about the wonders of quantum physics appear periodically on Habré: quantum eraser and weak measurements. Unfortunately, too often they are spoken of as mysterious and incomprehensible phenomena that make it possible to create almost magic, although in reality there is absolutely nothing surprising in them. In this post, I am translating an article by Sean Carroll on deferred quantum eraser. Let it be the starting point for discussion in the comments of all the tricks of quantum mechanics.
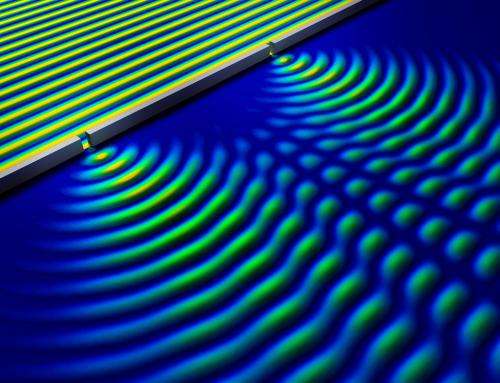
Let's imagine that you are a physics student, sitting on a course in experimental work, and the professor is in a particularly bad mood. It forces you to carry out a particularly strange version of Jung’s experience , explaining that this version is called a “delayed-choice quantum eraser.” You seem to have seen something like this on YouTube once.
In Jung’s traditional experiment with two slits, an electron beam passes through two slits and enters the recording screen. Each electron individually leaves a dot on the screen, but if we wait until a lot of such events are typed, we will see an interference picture with light and dark stripes. This is because the wave function of electrons passes through both slits and interferes with itself.
If we measure through which gap each electron passes, the interference image will disappear, and we will see a smoothed distribution on the screen. Textbooks on quantum mechanics will traditionally tell us that this happened due to the collapse of the wave function when we observed it on slits. The multi-world interpretation says that this is because the electron messed up with the measuring device, and the device messed up with the environment (decoherence occurred), and the wave function was divided into two separate worlds, in each of which the electron passed through only one of the slits.
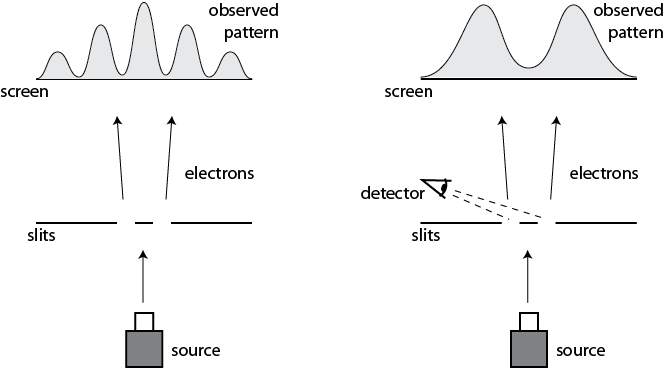The interference picture is visible when the electron passes through two slots (on the left), until an attempt is made to measure through which slit the electron passes (on the right).
Your experiment is complicated: you will measure through which gap an electron passes, but not with a large macroscopic device, but with a quantum device, and store information in a qubit. For example, for each “main” electron passing through the slits, we have a second “auxiliary” electron entangled with the first. The pair is confused as follows: if the main electron passes through the left gap, the auxiliary electron is in a state with spin up, and if through the right - with spin down:
Ψ = (L) [↑] + (R) [↓].
Your professor, who is obviously not in the mood today, insists that you do not take measurements on the "auxiliary" electrons, and do not even let them fly away and crash into something in the room. You carefully catch and store them, for example, in a magnetic trap.
What will we see on the screen if we repeat such an experiment with many electrons? Of course, a smooth distribution without an interference image, of course. Interference can occur only if two parts are components of the same wave function, and since two main electrons are now entangled with auxiliary ones, the paths through the left and right slots are distinguishable, and we do not see the interference picture. In this case, it turns out to be indifferent that we did not have a real dimension (and decoherence), but only confusion. The only important thing is that the main electrons are in a state of entanglement with auxiliary electrons. Any confusion kills interference.
Of course, we can measure the spins of auxiliary electrons if we want. If we measure them along the vertical axis, we get [↑] or [↓]. Regarding the quantum state Ψ, this will put us either in the universe where the main electron passed through the left gap, or in the universe where it passed through the right one. Finally, if we repeat the experiment many times, we will not see interference.
Okay, says your professor with sadistic inclinations, rubbing his hands with a villainous grin. Let's now measure our auxiliary electrons, but not along the vertical, but along the horizontal axis. The state in the vertical and horizontal bases are related as:
[↑] = [→] + [←],
[↓] = [→] - [←].
(For simplicity, we discard the normalization factors). In this basis, the same state as above will look like this:
Ψ = (L) [→] + (L) [←] + (P) [→] - (P) [←]
= ( + ) [→] + ( - ) [←].
When we measured the auxiliary spin in the vertical direction, we obtained a certain path of the main electron: [↑] was entangled with (), and [↓] was entangled with (). Making a measurement, we found out whether the main electron passed through the left or right slit. Now we measure the spin along the horizontal direction, and this certainty disappears. After the measurement, we again find ourselves in the branch of the wave function, where the main electron passes immediately through two slots. If we measured the spin “left”, the main electron will receive a phase shift when passing through the right slit (minus sign), but this is a purely mathematical feature.
So, choosing this method of measurement, we “erased” the information about the gap through which the electron passed. This is the so-called "quantum eraser." The erase process itself does not change the overall distribution of points on the screen. It remains smooth, and interference does not occur: the measurement results “left” and “right” are still random.
But now we have not only the general distribution of electrons on the screen. For each point on the screen, we also know the measurement result for the auxiliary electron: it was in the “spin to left” or “spin to right” state. So, your professor is blooming, let's now go to the computer and divide our measurements into two parts: the part for which the auxiliary electron had a spin to the left, and the part for which it was to the right. What will we see now?
Curiously, interference now reappears. The main electrons associated with auxiliary electrons with a left spin form an interference picture, as well as those for which the auxiliary electron had a spin to the right. (Remember that the interference image does not appear immediately, but appears as single electron statistics are collected). But these two pictures are shifted relative to each other, so that the peaks in one picture coincide with the dips in the other. When they are superimposed on each other, a smooth distribution occurs where the interference image is actually hidden.
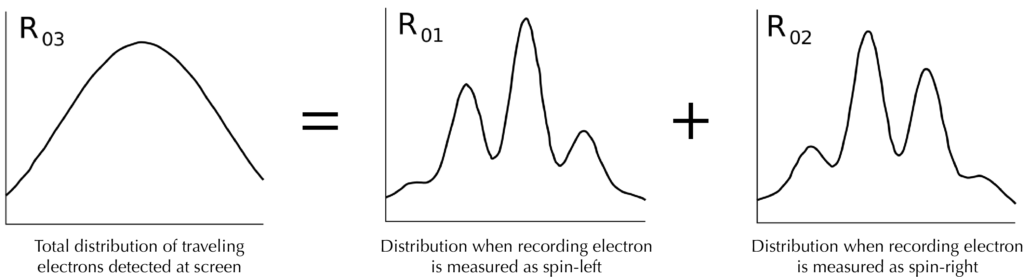Taken from Wikipedia
Looking back, we will not find it so surprising. If we look at how the state Ψ was recorded relative to auxiliary electrons in a horizontal basis (spin left or right), we see that each measurement was entangled with the main electron passing through both slots. So of course, interference could arise. And that minus, which seemed like a completely unimportant mathematical detail, shifted one picture relative to another so that when superimposed, they formed a smooth picture.
Your professor seems to be more surprised at this than you. “Can't you see!” She exclaims excitedly. “If we do not measure auxiliary electrons at all, or measure them along the vertical axis, no interference arises. And if we measure them along the horizontal axis, it turns out there was a hidden interference that we could detect by dividing the measurement results into parts for different spins of the auxiliary electron. ”
You and other students nod in agreement, although you are in some perplexity.
“Think about what that means! The choice of the direction of measurement of auxiliary spins could be made after all the main electrons were registered on the screen. If we saved all the auxiliary backs without letting them get confused with the surroundings, we could make this choice years later. ”
It seems yes, the audience mutters, it seems to be true.
“But interference only occurs when the main electrons pass through both slits, and a smooth distribution occurs when an electron passes through one slit. This decision - to pass through two slits or through one - occurs long before we measured the auxiliary electrons. Obviously, our decision to measure them horizontally, rather than vertically, sent a signal back to the past and informed the main electrons that they had to go through both slots at once, and not through one. ”
The puzzled audience freezes for a moment and explodes in protest. Decision? Back to the past? What are you talking about? The electron does not make the choice to go through one gap or another. Its wave function (and everything with which it is confused) evolves in accordance with the Schrödinger equation, as usual. An electron does not make choices, it definitely always passes through both slots, but it turns out to be in an entangled state. By measuring auxiliary electrons along different directions, we can choose different parts of the entangled wave function, some of which interfere, and some not. Nothing has returned to the past. This is a cool experiment, but no one is building any time machine here.
You and your comrades are right. Your professor is a little carried away. There is always the temptation to think of the electron as having something “wave and particle properties at the same time,” and the Copenhagen interpretation of quantum mechanics only condones this. If we succumb to this temptation, the idea that the electron behaves either as a particle or as a wave, and in each experiment one of these two options is realized, is not far off. And from this position, a quantum eraser with a delayed choice really leads to the conclusion that the information should have been transferred back to the past to help the electron with the choice. Honestly, popular explanations often complicate the picture, creating an aura of mystery in quantum mechanics. And the assumption that quantum mechanics allows you to send signals to the past only adds fuel to the fire.
All these temptations must be resisted. An electron is simply part of the wave function of the universe. He does not make the choice to be a particle or a wave. But for some reason, even serious researchers in the fundamentals of quantum physics sometimes consider experiments with a quantum eraser with a delayed choice and others like it (which, incidentally, have been repeatedly tested in practice) as evidence of reverse causality in nature - signals propagating backward in time, affect the past. A variant of such an experiment, proposed by none other than John Wheeler, suggested several telescopes on the other side of the screen that could determine which gap the electron passed through, much later than the moment it passed. Unlike later commentators, Wheeler did not go so far as to suggest reverse causality, and did not insist that the electron is always either a particle or a wave.
There is no need for reverse causality to explain a deferred quantum eraser. For the follower of a multi-world interpretation, the result is obvious without any time travel. The trick is that when entangled with one spin, and not a huge ensemble of particles in a classical detector and environment, the electron does not decohere in the full sense of the word. When the main electron is entangled with only one particle, we can consider different options for measuring this auxiliary particle. If, as in Jung’s usual experiment, we measured the gap through which an electron passed using a classical macroscopic device, we don’t have such a choice of measurement options. With true decoherence, the tiny size of the original entanglement is reinforced, essentially irreversibly, into entanglement with the environment. In this sense, a delayed-choice quantum eraser proves to be a useful thought experiment for understanding the role of decoherence and environment in measurements.
Unfortunately, not everyone is a proponent of a multi-world interpretation. In other versions of quantum mechanics, wave functions actually collapse, in contrast to the multi-world interpretation, where the collapse is only apparent, arising due to decoherence. In interpretations where the collapse actually occurs (such as GRW), it turns out to be asymmetric in time: the wave functions collapse, but cannot return to their original state. If in your theory there is a collapse of the wave function, but at the same time you want to maintain general time symmetry in the laws of physics, you can convince yourself of the need for reverse causality.
Or you can accept the smooth evolution of the wave function with branching rather than collapse, and automatically maintain time symmetry for all the basic equations without the need for time travel or doubting electrons.
Welcome to the Many Worlds!
From the translator. Sean Carroll is a professor at Caltech, specializing in cosmology and the basics of quantum physics. He is a consistent proponent of the Many-Worlds Interpretation (MMI) of quantum mechanics, about which Something Deeply Hidden recently released. Accordingly, the explanation of the experiment in the post will be from the standpoint of MMI. Although by and large this is not so important for the explanation itself. You can read my recent post about MMI if you want to refresh the basics.This article is a chapter from Something Deeply Hidden , not included in the final version of the text.
Carroll is also hosting a great Mindscape podcast. This podcast turned out to be almost the main event of my intellectual life in the last year, and, honestly, this is the best that you can get out of this post.
Disclaimer! In some places I adapted a little text, and added a little bit from myself for the sake of clarity. All errors are on my conscience (and in PM, I hope).
Let's imagine that you are a physics student, sitting on a course in experimental work, and the professor is in a particularly bad mood. It forces you to carry out a particularly strange version of Jung’s experience , explaining that this version is called a “delayed-choice quantum eraser.” You seem to have seen something like this on YouTube once.
In Jung’s traditional experiment with two slits, an electron beam passes through two slits and enters the recording screen. Each electron individually leaves a dot on the screen, but if we wait until a lot of such events are typed, we will see an interference picture with light and dark stripes. This is because the wave function of electrons passes through both slits and interferes with itself.
If we measure through which gap each electron passes, the interference image will disappear, and we will see a smoothed distribution on the screen. Textbooks on quantum mechanics will traditionally tell us that this happened due to the collapse of the wave function when we observed it on slits. The multi-world interpretation says that this is because the electron messed up with the measuring device, and the device messed up with the environment (decoherence occurred), and the wave function was divided into two separate worlds, in each of which the electron passed through only one of the slits.
The interference picture is visible when the electron passes through two slots (on the left), until an attempt is made to measure through which slit the electron passes (on the right).
Your experiment is complicated: you will measure through which gap an electron passes, but not with a large macroscopic device, but with a quantum device, and store information in a qubit. For example, for each “main” electron passing through the slits, we have a second “auxiliary” electron entangled with the first. The pair is confused as follows: if the main electron passes through the left gap, the auxiliary electron is in a state with spin up, and if through the right - with spin down:
Ψ = (L) [↑] + (R) [↓].
Your professor, who is obviously not in the mood today, insists that you do not take measurements on the "auxiliary" electrons, and do not even let them fly away and crash into something in the room. You carefully catch and store them, for example, in a magnetic trap.
What will we see on the screen if we repeat such an experiment with many electrons? Of course, a smooth distribution without an interference image, of course. Interference can occur only if two parts are components of the same wave function, and since two main electrons are now entangled with auxiliary ones, the paths through the left and right slots are distinguishable, and we do not see the interference picture. In this case, it turns out to be indifferent that we did not have a real dimension (and decoherence), but only confusion. The only important thing is that the main electrons are in a state of entanglement with auxiliary electrons. Any confusion kills interference.
Of course, we can measure the spins of auxiliary electrons if we want. If we measure them along the vertical axis, we get [↑] or [↓]. Regarding the quantum state Ψ, this will put us either in the universe where the main electron passed through the left gap, or in the universe where it passed through the right one. Finally, if we repeat the experiment many times, we will not see interference.
Okay, says your professor with sadistic inclinations, rubbing his hands with a villainous grin. Let's now measure our auxiliary electrons, but not along the vertical, but along the horizontal axis. The state in the vertical and horizontal bases are related as:
[↑] = [→] + [←],
[↓] = [→] - [←].
(For simplicity, we discard the normalization factors). In this basis, the same state as above will look like this:
Ψ = (L) [→] + (L) [←] + (P) [→] - (P) [←]
= ( + ) [→] + ( - ) [←].
When we measured the auxiliary spin in the vertical direction, we obtained a certain path of the main electron: [↑] was entangled with (), and [↓] was entangled with (). Making a measurement, we found out whether the main electron passed through the left or right slit. Now we measure the spin along the horizontal direction, and this certainty disappears. After the measurement, we again find ourselves in the branch of the wave function, where the main electron passes immediately through two slots. If we measured the spin “left”, the main electron will receive a phase shift when passing through the right slit (minus sign), but this is a purely mathematical feature.
So, choosing this method of measurement, we “erased” the information about the gap through which the electron passed. This is the so-called "quantum eraser." The erase process itself does not change the overall distribution of points on the screen. It remains smooth, and interference does not occur: the measurement results “left” and “right” are still random.
But now we have not only the general distribution of electrons on the screen. For each point on the screen, we also know the measurement result for the auxiliary electron: it was in the “spin to left” or “spin to right” state. So, your professor is blooming, let's now go to the computer and divide our measurements into two parts: the part for which the auxiliary electron had a spin to the left, and the part for which it was to the right. What will we see now?
Curiously, interference now reappears. The main electrons associated with auxiliary electrons with a left spin form an interference picture, as well as those for which the auxiliary electron had a spin to the right. (Remember that the interference image does not appear immediately, but appears as single electron statistics are collected). But these two pictures are shifted relative to each other, so that the peaks in one picture coincide with the dips in the other. When they are superimposed on each other, a smooth distribution occurs where the interference image is actually hidden.
Taken from Wikipedia
Looking back, we will not find it so surprising. If we look at how the state Ψ was recorded relative to auxiliary electrons in a horizontal basis (spin left or right), we see that each measurement was entangled with the main electron passing through both slots. So of course, interference could arise. And that minus, which seemed like a completely unimportant mathematical detail, shifted one picture relative to another so that when superimposed, they formed a smooth picture.
Your professor seems to be more surprised at this than you. “Can't you see!” She exclaims excitedly. “If we do not measure auxiliary electrons at all, or measure them along the vertical axis, no interference arises. And if we measure them along the horizontal axis, it turns out there was a hidden interference that we could detect by dividing the measurement results into parts for different spins of the auxiliary electron. ”
You and other students nod in agreement, although you are in some perplexity.
“Think about what that means! The choice of the direction of measurement of auxiliary spins could be made after all the main electrons were registered on the screen. If we saved all the auxiliary backs without letting them get confused with the surroundings, we could make this choice years later. ”
It seems yes, the audience mutters, it seems to be true.
“But interference only occurs when the main electrons pass through both slits, and a smooth distribution occurs when an electron passes through one slit. This decision - to pass through two slits or through one - occurs long before we measured the auxiliary electrons. Obviously, our decision to measure them horizontally, rather than vertically, sent a signal back to the past and informed the main electrons that they had to go through both slots at once, and not through one. ”
The puzzled audience freezes for a moment and explodes in protest. Decision? Back to the past? What are you talking about? The electron does not make the choice to go through one gap or another. Its wave function (and everything with which it is confused) evolves in accordance with the Schrödinger equation, as usual. An electron does not make choices, it definitely always passes through both slots, but it turns out to be in an entangled state. By measuring auxiliary electrons along different directions, we can choose different parts of the entangled wave function, some of which interfere, and some not. Nothing has returned to the past. This is a cool experiment, but no one is building any time machine here.
You and your comrades are right. Your professor is a little carried away. There is always the temptation to think of the electron as having something “wave and particle properties at the same time,” and the Copenhagen interpretation of quantum mechanics only condones this. If we succumb to this temptation, the idea that the electron behaves either as a particle or as a wave, and in each experiment one of these two options is realized, is not far off. And from this position, a quantum eraser with a delayed choice really leads to the conclusion that the information should have been transferred back to the past to help the electron with the choice. Honestly, popular explanations often complicate the picture, creating an aura of mystery in quantum mechanics. And the assumption that quantum mechanics allows you to send signals to the past only adds fuel to the fire.
All these temptations must be resisted. An electron is simply part of the wave function of the universe. He does not make the choice to be a particle or a wave. But for some reason, even serious researchers in the fundamentals of quantum physics sometimes consider experiments with a quantum eraser with a delayed choice and others like it (which, incidentally, have been repeatedly tested in practice) as evidence of reverse causality in nature - signals propagating backward in time, affect the past. A variant of such an experiment, proposed by none other than John Wheeler, suggested several telescopes on the other side of the screen that could determine which gap the electron passed through, much later than the moment it passed. Unlike later commentators, Wheeler did not go so far as to suggest reverse causality, and did not insist that the electron is always either a particle or a wave.
There is no need for reverse causality to explain a deferred quantum eraser. For the follower of a multi-world interpretation, the result is obvious without any time travel. The trick is that when entangled with one spin, and not a huge ensemble of particles in a classical detector and environment, the electron does not decohere in the full sense of the word. When the main electron is entangled with only one particle, we can consider different options for measuring this auxiliary particle. If, as in Jung’s usual experiment, we measured the gap through which an electron passed using a classical macroscopic device, we don’t have such a choice of measurement options. With true decoherence, the tiny size of the original entanglement is reinforced, essentially irreversibly, into entanglement with the environment. In this sense, a delayed-choice quantum eraser proves to be a useful thought experiment for understanding the role of decoherence and environment in measurements.
Unfortunately, not everyone is a proponent of a multi-world interpretation. In other versions of quantum mechanics, wave functions actually collapse, in contrast to the multi-world interpretation, where the collapse is only apparent, arising due to decoherence. In interpretations where the collapse actually occurs (such as GRW), it turns out to be asymmetric in time: the wave functions collapse, but cannot return to their original state. If in your theory there is a collapse of the wave function, but at the same time you want to maintain general time symmetry in the laws of physics, you can convince yourself of the need for reverse causality.
Or you can accept the smooth evolution of the wave function with branching rather than collapse, and automatically maintain time symmetry for all the basic equations without the need for time travel or doubting electrons.
Welcome to the Many Worlds!
All Articles