Riddles on the quest for perfect chance

Is there an objective, ideal chance, or is it the result of our ignorance?

Life is unpredictable, and accidents happen to us all the time. We can say that the universe itself is accidental. And yet, somehow, large numbers of random events can create large-scale patterns that science can predict. Heat dissipation and Brownian motion are just two examples of such events.



Recently, randomness even fell into the news feeds: it turned out that random surfaces have a hidden order , and we may also have come close to seeing how a quantum computer generates perfect randomness . The latter case, the search for perfect randomness, is important because randomness brings unpredictability, and all non-quantum technology attempts to achieve it have one hidden flaw: they are implemented using algorithms that, theoretically, can be decrypted. In this column, we will learn how to create randomness and defeat it in everyday life, before going up to the philosophical heights of the debate about what is true randomness.

Riddle 1: random combinations

Consider a simple code lock for a bicycle, similar to the above image. It has three rotating disks, each of which shows 10 digits in order. When these three discs are rotated so as to give the desired combination - 924 - the lock opens. When you want to close it, you need to mix the numbers so that they are far away from the given combination. But what does “far” mean in this context? If you move the disk as much as possible by 5 positions, you will set the number 479. However, it will be easy for an attacker to accidentally stumble upon this position if he simply turns all five disks at the same time and sees if the lock opens. Imagine that a cracker has time to test five different combinations. In each case, our potential thief tries our castle after one of the following actions (and in case of failure, returns the castle to its original configuration):

• Rotate one drive at a random number of positions.
• Rotate two discs simultaneously at a random number of positions.
• Rotate all three disks at the same time at a random number of positions.
• Rotate two discs at different angles.
• Rotate all three discs differently.,

Our riddle is the following: if the lock unlock code is 924, which set of mixed numbers will be the most stable for random attempts to open the lock, and how many such sets exist? What is the probability of detecting code?

Riddle 2: from randomness to order in riddles

It often surprises me how similar the process of solving the puzzle to scientific progress is. We go from randomness to order, adding pieces, and our confidence in the correctness of the decision is fueled with each new suitable piece. In the second task, we will try to create a way to measure our progress on the way from a random disordered state to a complete, ordered solution.







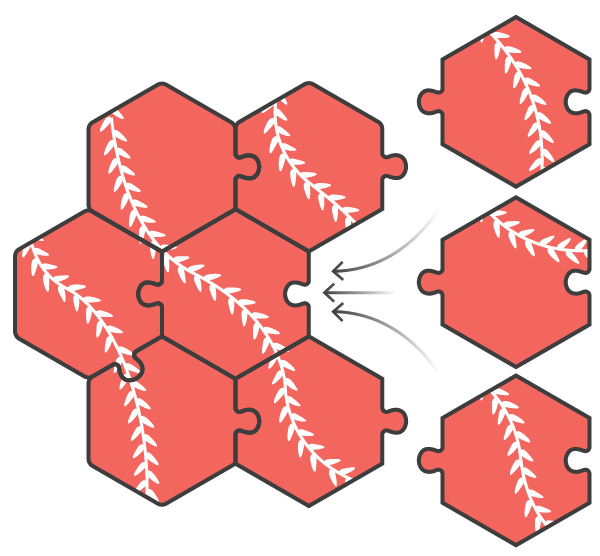
Suppose we solve a puzzle consisting of hexagonal pieces - like honeycombs. The picture of the puzzle is a winding vine. Since the pattern is repeating and self-similar, it cannot be guaranteed that two adjacent pieces fit physically to each other, even if they fit the picture. Suppose that three others can go to each edge of a given piece. Therefore, when two pieces fit each other in the picture, the probability that they fit physically will be 33.33%. However, if you can find another piece that fits both of these, that is, one that has one common edge with each of these two, then your confidence in success will increase. Let's try to evaluate how much it grows.

1. You have found three pieces that seem to fit together at first glance, without the obvious displacement of the liana pattern on their adjoining edges. What is the measure of your confidence in the correct selection of pieces?
2. You have found a central hexagonal piece, and six surrounding it, and in the picture they seem to coincide. What is the measure of your confidence in the correct selection of pieces?

The larger the groups of pieces become, the stronger your confidence in the correct assembly. It is reasonable to assume that three isolated groups, in which there are a total of seven connected pieces, are not comparable with the only surrounded hexagon described above.



The third part of this puzzle has corrections, and is an attempt to quantify the above difference. Is it possible to come up with a measure of the degree of completion of a partially solved puzzle? This method should allow you to assign a number from 0 to 100 to any partially assembled puzzle of 10x10 hexagons. This number should indicate the degree of completion, roughly correlating with the proportion of the current state of the puzzle in relation to the finished version.

Riddle 3: is perfect coincidence possible?

For this part, I will give you a variant of the famous Einstein-Bohr debate for chance. Debate participants can join teams E or B.



Both teams agree that in the macrocosm the existence of random-generating mechanisms is possible only because we do not understand the forces, or the algorithms underlying them. If you knew all the forces acting on a flipped coin or a dice, then if you had sufficient computing power, you could predict the result. We are taught, according to the prevailing views of team B, that this is not so in the quantum world - quantum probabilities must be objective. But is this even possible? Could there be some mechanism in the subquantical Planck world that decides which of the two equally probable options will be implemented, even if we never have the opportunity to study this level? Even if Einstein’s nightmare with a dice playing dice is real, this deity should have some algorithm in his head that decides each choice, no matter how bizarre and illogical it is. Then chance will again be due to our ignorance. It will be unknown only in practice, and not randomly objective.



The standard response from Team B is that the quantum world is simply too strange to apply to it the rules we have learned from our experience in interacting with the macrocosm. However, there are two kinds of oddities. On the one hand, strangeness may lie in the physical impossibility of traveling faster than the speed of light. Such a strangeness can exist, and it will only mean that we need to reconsider our understanding of the physical law in special circumstances, just as Einstein revised the law of addition of Newton's velocities, which becomes incorrect at very large values.



On the other hand, something may be strange in terms of logical impossibility - such as 2 + 2 equals 5. Such a result is impossible in any universe. Team E may argue that perfect chance and objective probabilities are logically impossible. We should not accept them, but instead we must find physical mechanisms that can explain the observed results, regardless of what existing laws of physics they may violate.



Which team do you join?



PS: Answers will be published later.