What lies behind the Feigenbaum constant

Obituary: Mitchell Feigenbaum, (1944-2019), 4.66920160910299067185320382 ...

Steven Wolfram Blog Article







It is called the Feigenbaum constant and equals approximately 4,6692016. And it occurs with enviable periodicity in certain types of mathematical - and physical - systems that can demonstrate chaotic behavior.



Mitchell Feigenbaum , who left us on June 30 at the age of 74, was the person who discovered it - in 1975, and he did this by doing experimental mathematics on a pocket calculator.



This discovery has become decisive in the theory of chaos . But when it was first discovered, this result was unexpected, bizarre, unrelated to anything from what was studied earlier. However, in some ways, the fact that it was Mitchell Feigenbaum who I had known for almost 40 years to discover it seems appropriate.



Mitchell, a student of theoretical physics, and a connoisseur of its mathematical traditions, always seemed to consider himself an outsider. He looked a little like Beethoven - and made an elegant impression of a certain intellectual secret. He often made strong statements, usually with a conspiratorial look, with a gleam in his eyes and a glass of wine or a cigarette in his hand.



He talked in long ornate sentences that betrayed him as an erudite and an intellectual. But the ideas from it poured the most different. Sometimes they were detailed and technical. Sometimes these were leaps of intuition, which, at least, I could not keep track of. He always read something, did not sleep until 5-6 hours, filling the yellow pages of notebooks with formulas and loading the Mathematica system with complex algebraic calculations that could last for hours.



He published little, and published works often disappointed him with the fact that not many people understood them. By the time of his death, he had worked for many years on optics of perception, and on such questions as “why does the moon seem larger when it is above the horizon”. However, he did not decide to publish anything like that.



For more than 30 years, Mitchell's official work (which he received, in fact, thanks to the opening of the Feigenbaum constant) was a professor at Rockefeller University in New York (to meet the Institute’s biological research mission, he was appointed head of the “Laboratory of Mathematical Physics”). However, he still did a lot of work, gave his name to the startup of financial computing, and was closely associated with the invention of new cartographic methods for the world-wide atlas Hammond .

What Mitchell discovered

The basic idea is pretty simple. Take the number x from 0 to 1. We will gradually replace x with ax (1 - x). Suppose we start with x = 1/3, and a = 3.2. Then here are the sequential values ​​of x we ​​will get:







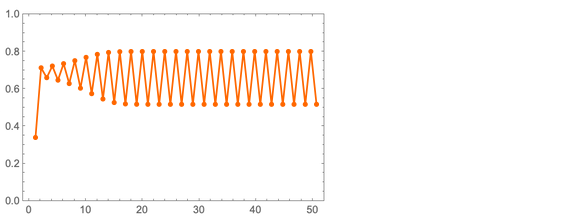
The values ​​of x quickly become periodic, with a period of 2. But what happens if we take other values ​​of a? Here are some results for the so-called "Logistic Mapping":







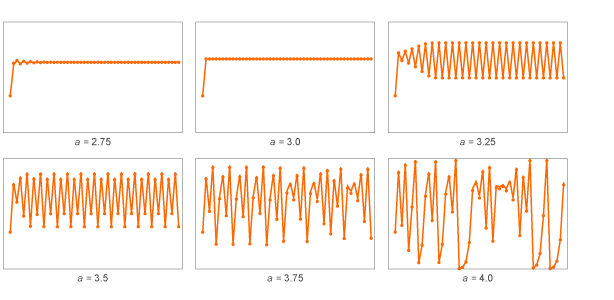
For small a, the values ​​of x quickly come to fixed values. For large a, they become periodic, first with a period of 2, then 4. And for larger a, the values ​​begin to jump with an apparently random way.



This can be summarized by constructing the values ​​of x (here they are 300, after discarding the first 50) as a function of the value of a:







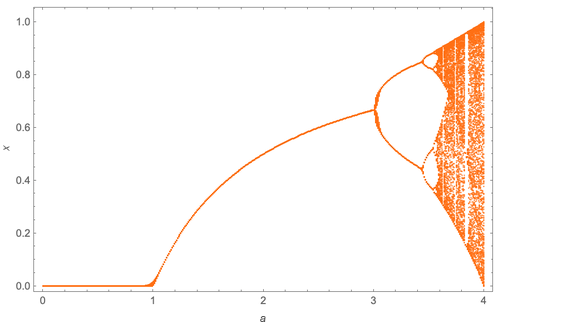
With increasing a, a cascade of period doubling is observed. In this case, they occur at a = 3, a ≈ 3.449, a ≈ 3.544090, a ≈ 3.5644072. Mitchell noted that these consecutive values ​​have a limit (a _∞ ≈ 3.569946) in the geometric sequence, a _∞ - a _n ~ δ ^-n and δ ≈ 4.669.



An interesting result. But here is what gives it meaning: this is true not only for a certain iterative mapping x → ax (1 - x); This is true for any display. Here, for example, is the “bifurcation diagram” for for x → a sin (π √x):







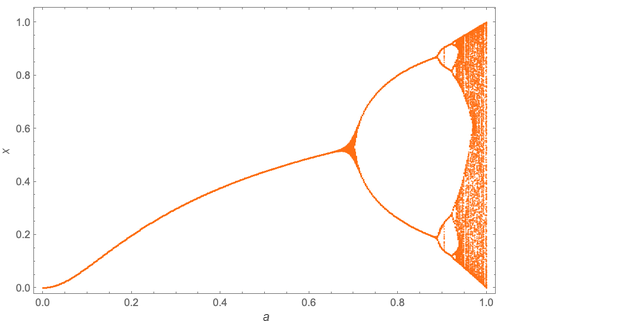
The details differ, but Mitchell noted that the arrangement of period doubling again forms a geometric sequence with exactly the same base δ ≈ 4.669.



And not only these various iterative mappings gave qualitatively similar results; when measuring the convergence rate, it turns out to be exactly the same - always δ ≈ 4.669. This was Mitchell's great discovery: a quantitatively universal feature of the approach to chaos in the class of systems.

Scientific background

The basic idea of ​​iterative mappings has a long history dating back to ancient times. Their early versions arose in connection with the search for successive approximations, for example, of square roots. For example, Newton’s method from the 17th century √2 can be obtained by iterations x → 1 / x + x / 2. Starting from x = 1:







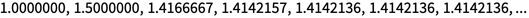
The idea of ​​an iterative approximation of an arbitrary function was first formalized, apparently, in the 1870 paper by Ernst Schroeder (known for formalizing many things, from degrees to Boolean algebra), although most of the discussions concerned the solution of functional equations and not the iterations themselves (except for the study areas of convergence of the Newtonian approximation done by Arthur Cayley in 1879). In 1918, Gaston Maurice Julia conducted an extensive study of iterative material functions on the complex plane, inventing the Julia set . But before the emergence of fractals in the late 1970s (which soon led to the appearance of the Mandelbrot set ), this area of ​​mathematics vegetated.



But regardless of the research in pure mathematics, iterative mappings with forms similar to to x → ax (1 - x) began to appear in the 1930s among possible practical models for studying population biology or the theory of business cycles. Usually they appeared in the form of discrete versions of continuous equations, such as the Verhulst logistic equation of the mid-19th century. Oscillatory behavior was also common - and in 1954, William Ricoeur (one of the founders of scientific fishing) also found more complex behavior when iterating through empirical fish reproduction curves.



In pure mathematics, variants of iterative mappings periodically arose in number theory. In 1799, Karl Friedrich Gauss , in fact, studied the mapping x → frac (1 / x) in connection with continued fractions. Since the end of the 19th century, interest has appeared in mappings of the form x → frac (ax) and their relation to the properties of a.



Immediately after the work of Henri Poincaré on effective methods of celestial mechanics in the 1900s, the idea of ​​sensitivity to initial conditions appeared, and in the end it was noticed that iterative maps can, in fact, “dig up numbers” in initial conditions. For example, iterating x → frac (10 x) over π digits essentially just shifts the sequence of digits one position to the left with each step:











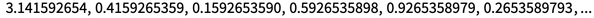
Mappings of the type x → ax (1-x) also demonstrate a similar “digging out of numbers” (for example, if x is replaced by sin (π u) ² , then x → 4 x (1-x) turns exactly into u → frac (u , 2), and this was already known in the 1940s - for example, John von Neumann commented on this in 1949 in connection with his iterative mid-square method for generating pseudorandom numbers by a computer.



However, what about experimental mathematics based on iterative mappings? There was virtually no experimental mathematics on early digital computers (the computer time of most of them was too expensive). But in the wake of the Manhattan project in Los Alamos, they created their own MANIAC computer, which eventually began to be used for a series of studies in the field of experimental mathematics. In 1964, Paul Stein and Stan Ulam wrote a report titled “Studying Nonlinear Transformations on Electronic Computers,” which shows photographs of MANIAC screens similar to those of oscilloscopes and which show iterative displays of a rather complex form. In 1971, another report created in Los Alamos “out of sheer curiosity” (written by Nick Metropolis, the head of the MANIAC project and the developer of the Monte Carlo method, as well as Paul Stein and his brother Miron Stein), produced more specific computational results for logistic mappings , and noted the basic phenomenon of period doubling (the authors called it the U-sequence), as well as the qualitative resistance to changes of the underlying display method.



Apart from all this in physics and mathematics there were other developments. In 1964, Ed Lorenz (meteorologist from MIT) introduced and created a simulation of his "naturally occurring" differential equations of his name, where sensitivity to initial conditions was demonstrated. Since the 1940s, a continuous stream of mathematical developments in the field of theory of dynamical systems has formed (the work was based on the achievements of Poincare from the 1900s). In particular, they investigated the global properties of solutions of differential equations. Usually, researchers encountered fixed points, sometimes limit cycles. However, by the 1970s, especially after the appearance of the first computer simulations (like Lorentz's), it became clear that something else could happen with nonlinear equations: the so-called " strange attractor ." And while studying the "returned mappings" of strange attractors, iterative mappings began to appear again.



However, it was not until 1975 that various studies of iterative mappings began to intersect. In the field of pure mathematics, dynamical systems theorist Jim York and his student Tien-Yen Lee from the University of Maryland published Chaos Follows from Period Three, where they showed that an iterative mapping with a certain parameter value, the initial condition of which leads to the appearance of a cycle of length three , there must be other initial conditions that do not lead to the appearance of cycles - or, as they describe it, demonstrating chaos. Then it turned out that Alexander Sarkovsky, a representative of the Soviet school of dynamic systems research, back in 1962, proved a slightly weaker result, in which cycles with all periods follow from a cycle with period 3.



At the same time, interest in mathematically oriented specialists in population biology began to grow in logistic mappings, from which the well-written 1976 review, Simple Mathematical Models with Very Complex Dynamics, was born, authored by an Australian physicist by education, Robert May , who at that time was a professor biology at Princeton (then he will become the scientific adviser to the British government and receive the title of Baron May of Oxford).



But although there were such things as sketches of bifurcation diagrams, the discovery of their universal numerical properties had to expect the appearance of Mitchell Feigenbaum.

Mitchell's Travel

Mitchell Feigenbaum grew up in Brooklyn, New York. His father was an analytical chemist, and his mother taught at a public school. Mitchell did not particularly like to study, although he received good grades in exams in mathematics and the exact sciences, and also independently learned matanalysis and playing the piano. In 1960, at the age of 16, he, like some prodigy, entered the city college of New York, officially to study electrical engineering, but also attended physics and mathematics courses. After graduating in 1964, he entered the MIT. At first he wanted to defend a doctorate in electrical engineering, but quickly switched to physics.



And although he was delighted with classical mathematical physics (such as that presented, for example, in the books of Landau and Lifshitz), he ended up writing a dissertation on the topic appointed by his curator - particle physics and an assessment of the class of Feynman diagrams for scattering photons by scalar particles . The dissertation was not very interesting, but in 1970 he was sent to Cornell University as a postdoc.



Mitchell started having problems with motivation, and instead of doing physics, he preferred to spend time in cafes, solving crosswords in the New York Times (which he managed to do with great speed). But at Cornell, Mitchell made some important friends. One of them was Predrag Tsvitanovic, an outstanding graduate student from that part of Yugoslavia that is now called Croatia; he studied quantum electrodynamics, and shared with Mitchell an interest in German literature. Another was the young poetess Kathleen Durish (who later became Katie Hammond), a friend of Predrag. Another was the rising star of physics, Professor Pete Carruthers, who shared with Mitchell an interest in classical music.



In the early 1970s, the golden age of quantum field theory was approaching. But, despite the theme of his work, Mitchell did not do this, and after two years in Cornell did not produce any results. However, he managed to impress Hans Bethe , and he transferred it to another place, also as a postdoc, but to an institute that occupies a slightly lower place in the unofficial hierarchy - the Virgin Polytechnic.



At the Virgin Institute, Mitchell did even less than at Cornell. He practically did not communicate with people, and gave out only one work on three pages: “The relationship of the normalization coefficient and the dispersion function in the transport equation of multigroups”. As the name implies, the work was technical and uninteresting.



At the end of Mitchell’s two-year stay in Virginia, it was not clear what would come next. However, luck intervened. Mitchell's friend from Cornell, Pete Carruthers, was hired to set up a theoretical unit in Los Alamos, and was given carte blanche to hire several prominent young physicists. Pete then proudly told me (as part of scientific management advice) that he had the feeling that Mitchell was capable of something great, and despite the opinions of other people - and the evidence - he decided to put on him.



Transferring Mitchell to Los Alamos, Pete began to offer him projects. At first, it was a continuation of Pete’s work, attempts to calculate a bunch of collective (“transport”) properties of quantum field theory in order to understand high-energy particle collisions — these were works that preceded studies of quark-gluon plasma.



But soon, Pete suggested that Mitchell deal with turbulence in liquids, in particular, to find out if the renormalization group methods would help.



When a liquid - for example, water - begins to flow fast enough, small whirlpools appear in it, and it begins to behave in a complex, and, at first glance, random way. But although this phenomenon has been discussed qualitatively for many centuries (for example, even Leonardo da Vinci made his sketches), physicists could tell about it remarkably little - although in the 1940s Andrei Nikolaevich Kolmogorov remarked that whirlpools should form a cascade with k - energy distribution. In Los Alamos, scientists focused on developing atomic weapons (which inevitably involves studying the behavior of fluids with strong currents), and turbulence was very important to understand - although it was not obvious how to approach it.



In 1974, news appeared that Kenneth Wilson of Cornell “solved the Kondo problem” [Kondo's problem is the inability of theoretical physics to explain the Kondo effect / approx. trans.] using a technique called "renormalization group." Pete Carruthers suggested that Mitchell apply this technique to turbulence.



The renormalization group is related to how changing the scale (or other parameters) affects the description (and behavior) of the systems. It so happened that Mitchell’s PhD from MIT, Francis Lowe, together with Murray Gel-Mann, reintroduced it in 1954 in the context of quantum electrodynamics. The idea lay motionless for many years, but returned in the 1970s, and was actively - albeit in different ways - applied both to particle physics (especially in quantum chromodynamics ) and to condensed matter physics.



In a piece of iron in the room, you can align the spins of all the electrons associated with each atom, and then the iron will be magnetized. But if you warm up the iron, fluctuations will begin in it, and suddenly - at a temperature above the so-called. Curie points (770 ° C for iron) - so much randomness appears in the iron that its magnetic properties disappear. In general, there are quite a few situations (melting, boiling, the formation of traffic congestion) when this sudden so-called phase transition .



But what exactly happens during the phase transition? I think the easiest way to see this is by studying its counterpart in the field of cellular automata. With the specific rule below, when the system initially does not have a large number of black cells, soon it will all turn white. But if you increase the number of original black cells (by analogy with increasing the temperature of the magnetic system), then suddenly, in this case, with a 50% proportion of black cells, a sharp transition occurs, and the whole system eventually turns black (observation for experts on phase transitions: yes , this is a phase transition in a one-dimensional system; a two-dimensional can only be needed if the system needs to be microscopically reversible ).







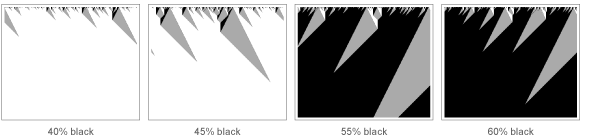
But what happens to the system near the border of 50% black cells? In fact, she cannot decide whether to become black or white. As a result, it shows a whole hierarchy of fluctuations, from the smallest to the largest. By the 1960s, it became clear that the “critical exponents” characterizing the power laws describing these fluctuations are the same for many systems.



But how do we calculate these critical exponents? In some artificial cases, analytical methods were known. But for the most part, something else was required. In the late 1960s, Ken Wilson realized that renormalization groups and computers could be used. It is possible to construct a model of the interaction of individual spins. But the renormalization group gives you a “scaling” procedure for interactions of more and more large blocks of spins. And by studying this on a computer, Ken Wilson managed to start calculating critical exponents.



At first, physicists did not pay due attention to this, not least because they were not used to such an active use of computers in theoretical physics. But then the Kondo problem arose. In most materials, the electrical resistance decreases with decreasing temperature (and in superconductors it decreases to zero even at temperatures above absolute zero). However, in the 1930s, measurements on gold showed that its resistance increases at low temperatures. By the 1960s, it was believed that the whole thing was the scattering of electrons by magnetic impurities - however, the calculations ran into trouble, giving out infinity in the results.



Then in 1975, Ken Wilson applied his methods of renormalization group - and was able to accurately calculate the effect. This effect is still shrouded in some mystery (probably due to the fact that I often had difficulty understanding Ken Wilson’s explanations on this topic, at least since I met him in the 1980s). But the idea that the renormalization group may be important has taken root.



How can it be applied to fluid turbulence? The Kolmogorov power law gave certain ideas. But was it possible to take the Navier-Stokes equations that control the flow of an idealized fluid and derive some of them? This project was taken up by Mitchell Feigenbaum.

Major discovery

Navier-Stokes equations are very difficult to work with. To this day, it is not very clear how even the most obvious property of turbulence - its apparent randomness - arises from them. Perhaps these equations are not a complete or consistent mathematical description, and we actually see enhanced microscopic movements of the molecules. Perhaps - as in the theory of chaos and the Lorentz equations - the whole thing is to enhance randomness in the initial conditions. Personally, based on my work from the 1980s, I believe that the whole point is in the properties of their internal calculations, similar to the randomness in my " rule 30 " for a cellular automaton.



How did Mitchell approach this problem? He tried to simplify it - first by moving from equations that depend on space and time to equations that depend only on time, and then making them discrete and studying iterative mappings. From Paul Stein, Mitchell was aware of previous work on iterative mappings done in Los Alamos (which was not widely known). But Mitchell did not understand which way to move on, although, having received at his disposal a brand new ultra-modern programmable calculator HP-65, he decided to program iterative displays on it



Then, in July 1975, Mitchell went to a summer physical meeting in Aspen, Colorado. There, he met with Stephen Smale, a famous mathematician who studied dynamical systems, and was surprised to learn that he was talking about iterative mappings. Smale mentioned that someone was asking him if the limit of a cascade with a doubling period a _∞ ≈ 3.56995 can be expressed in terms of standard constants like π and √2. Smale did not know the answer to this question. However, Mitchell became interested in this, and decided to try to find out the answer.



He did not have the HP-65 with him, but he plunged into this issue using standard tools of an educated mathematical physicist, and soon turned the task into a search for function poles on the complex plane, which he had nothing to say about. However, returning to Los Alamos in August, he turned to his HP-65, and began to program it in order to detect bifurcation points a _n .



For small n, the iteration went pretty fast. For n = 5, it took 30 seconds. For n = 6, I had to wait several minutes already.However, while the calculator was working, Mitchell decided to look at the values ​​of a _n that he already had, and noticed something: they seemed to geometrically strive for some final value.



At first, he simply used this fact to estimate a _∞ , which, despite all attempts, he could not express through standard constants. But he soon began to suspect that the convergence exponent δ was more important than a _∞ - since its value remained unchanged with simple changes in the variables in the map. For about a month, Mitchell tried to express δ in terms of standard constants.



But then, in October 1975, he remembered that Paul Stein said that doubling the period looks the same not only for logistic mappings, but generally for all iterative mappings with one maximum. Having reunited with his HP-65 after a trip to Caltech, Mitchell immediately tried the display x → sin (x) and found that the exponent δ was exactly the same as three decimal places.



He immediately decided that he had stumbled upon something wonderful. But Stein said he would need more numbers to draw conclusions. There were a lot of powerful computers in Los Alamos, so the next day Mitchell asked someone to show him how to write a FORTRAN program to move on - and by the end of the day he was able to calculate that in both cases δ had a value of about 4.6692 .



The computer he used was a typical workhorse for US science in those days: the CDC 6000 model (the same type that I used when I first moved to the USA in 1978). It was developed by Seymour Cray, and by default she used 60-bit floating point numbers. But with such accuracy (14 digits after the decimal point) Mitchell could not get anything better than 4.6692. Fortunately, Pete's wife, Lucy Carruthers, was a Los Alamos programmer, and she showed Mitchell how to use double precision. As a result, he was able to calculate δ up to 11 decimal places, and determine that the values ​​of two different iterative mappings are the same.



Over the course of several weeks, Mitchell discovered that δ appears to be a universal value for all iteration maps with one quadratic maximum. But he did not know why this was happening, and he did not have any specific mathematical apparatus for studying this issue. But in the end, at the age of 30, Mitchell discovered something that seemed really interesting to him.



On his birthday on December 19, Mitchell met with his friend Predrag and told him about this result. However, at that time, Predrag was working with mainstream particle physics, and he did not attach much importance to this.



Mitchell continued to work, and after a few months he became convinced that not only the exponent δ was universal - with the proper scale, the iterative mappings themselves were universal. In April 1976, Mitchell wrote a report on his results. On May 2, 1976, he talked about them in a lecture at the Advanced Research Institute in Princeton. Predrag was there, and then he finally became interested in Mitchell's work.



But Predrag quite often was not clear what Mitchell was talking about. But the next day, Predrag successfully managed to simplify the problem and obtain one immediate functional equation for the limited form of the scaled iteration map: g (g (x)) = -g (α x) / α, where α ≈ 2.50290, which implies that for any iterative mapping of a certain type, its limited form will look like a more tortuous version of this mapping:

How everything developed

The field of research on iterative mappings gained momentum on June 10, 1976 after publishing a review in the journal Nature by Robert May, which he wrote independently from Mitchell, and, naturally, without mentioning the results he obtained. But in the months that followed, Mitchell traveled with his reports on his results. The reaction to them was mixed. Physicists were interested in how these results relate to physics. Mathematicians did not understand their status, given that they were obtained from experimental mathematics and did not have formal mathematical proof. And, as usual, it was difficult for people to understand Mitchell's explanations.



In the fall of 1976, Predrag got a postdoc at Oxford, and on the very first day I arrived there, a 17-year-old student writing a diploma in particle physics, I met with him. We mainly talked about his elegant “bird footprint” method for working with group theory (the book about which he finally published 32 years later). He also tried to explain iterative maps to me. And I still remember how he talked about the idealized model of fish population in the Adriatic (only after years I connected this with the fact that Predrag was from those places that are now called Croatia).



At that time I did not attach any importance to this, but the idea of ​​iterative mappings became entrenched in my mind, and soon mixed up with the idea of ​​fractals, which I learned from the book of Benoit Mandelbrot. And when, after a couple of years, I concentrated on the problems of complexity, these ideas helped me to come to such systems as cellular automata.



But in 1976, Mitchell (until my next meeting, which will take several more years) actively traveled with reports on the results. He also submitted work to the prestigious scientific journal Advances in Mathematics. For six months he did not receive news from there, but in the end the work was rejected. He tried again, sending another job to SIAM Journal of Applied Mathematics - with the same result.



I want to say that I am not surprised by this. In my experience of publications in academic literature (which I have not been doing for a very long time), publishing a work in a defined field of research is quite easy. But work in the field of something truly new or original can practically rely on rejecting it after an expert assessment - either because of intellectual shortsightedness or because of academic corruption. Mitchell had another problem - his explanations were hard to understand.



But finally, in 1977, Joel Lebovitz, editor of the Journal of Statistical Physics, agreed to publish Mitchell's work - in fact, because he met him, because he admitted that he did not understand the work. So the 1978 work “Quantitative Universality in the Class of Nonlinear Transformations” appeared, describing Mitchell's great achievement. In order to set academic priorities, Mitchell sometimes cited a summary of the report he made on August 26, 1976, and published in the Los Alamos Theoretical Division annual collection of reports for 1975-1976. Mitchell was greatly influenced by the refusals to publish his works, and for years he kept letters of refusal in a drawer.



Mitchell continued to travel around the world with reports on the results. There was interest in them, but there was bewilderment. However, something amazing happened in the summer of 1979: Albert Liebhaber from Paris reported the results of a physical experiment on the transition to turbulence in convective flows of liquid helium, where he saw a doubling of the period exactly with the exponent δ that Mitchell calculated. It turned out to be universal not only for the class of mathematical systems, but also proved to be in real, physical systems.



And instantly Mitchell became famous. A connection with the renormalization group was discovered, his work became fashionable for both physicists and mathematicians. Mitchell continued to ride with reports, but now he had the opportunity to regularly hang out with the best physicists and mathematicians.



I remember how he came to Caltech, sometime in the fall of 1979. All this resembled a meeting with a rock star. Mitchell arrived, made a stylish, but a little mysterious report, and then Richard Feynman and Murray Gell-Man stole him for a private conversation .



Soon, Mitchell was offered a bunch of different upscale jobs, and in 1982 he returned with triumph to Caltech as a professor of physics. There was talk that the discovery was worthy of a Nobel prize, and by June 1984 he appeared in the New York Times magazine, with Beethoven's chic, amid a Cornell waterfall:







But mathematicians remained unhappy. As in the case of Benoit Mandelbrot's work, they considered Mitchell's results to be “numerical hypotheses”, unproven, and unworthy of mention. However, the best mathematicians (with whom Mitchell made friends) soon began to work on this problem, and the results were not long in coming - although it took ten years to complete and final proof of the universality of δ.

Where did science go

What happened to Mitchell’s major discovery? It, of course, became famous. And cascades with period doubling with its universal properties were soon found in a number of systems - in liquids, optics, etc. But how common were they? Could they be extended to the whole problem of turbulence in a fluid?



Mitchell and others studied systems other than iterative mappings and found related phenomena. But among them were not as surprising as Mitchell's first discovery.



In a sense, my attempts to study cellular automata and the behavior of simple programs, begun in 1981, were aimed at searching for some of the big questions that Mitchell's work could lead to. However, our methods and results were very different. Mitchell always tried to stay close to such things that traditional mathematical physicists can turn to, and I fearlessly went into the computing universe, exploring the phenomena encountered there.



I tried to understand how Mitchell’s work could be related to mine, and in my first work on cellular automata in 1981, I even noted, for example, that the average density of black cells in successive steps in the evolution of a cellular automaton can be estimated approximately through iterative mapping.



I also noted that mathematically the entire evolution of a cellular automaton can be considered as an iterative map - although not on a set of ordinary real numbers, but on a cantor set . In my first work, I even built an analogue of Mitchell smooth mappings, but they were wild and discontinuous in me:







But, no matter how I tried, I still could not find explicit connections with Mitchell's work. I was looking for analogues of the doubling of the period or Sharkovsky orderbut found nothing special. For my computing platform, even thinking about real numbers with their infinite sequences of numbers was unnatural. Many years later, in the book “A New Kind of Science”, I inserted the note “Smooth Iterative Mapping”. I showed their sequence of numbers and observed how Mitchell's discovery implies the presence of an unusual nested structure at the beginning of the sequences:

End of story

What happened to Mitchell? After spending four years in Cornell, he moved to Rockefeller University in New York, and for the next 30 years led an almost bohemian existence, spending most of his time in his apartment in Upper East Side in Manhattan.



While in Los Alamos, Mitchell married a woman of German descent named Cornelia, the sister of physicist (and my long-time friend) David Campbell, who founded the Center for Nonlinear Studies in Los Alamos, and then became rector of Boston University. However, rather quickly, Cornelia left Mitchell, and to none other than Pete Carruthers. Later, Pete, suffering from alcoholism and other problems, reunited with his wife Lucy, but died in 1997 at the age of 61.



In Cornell, Mitchell met Gunilla, who, at the age of 14, escaped from a pastor's family from a small town in northern Sweden, and at first was a model with Salvador Dali, and then came to New York as a fashion model in 1966. Gunilla was a journalist, videotaped, wrote plays and painted pictures. They married Mitchell in 1986, and their marriage lasted 26 years, during which Gunilla made a good career in figurative art .



The latest work, written by Mitchell on his own, was published in 1987. He also published many works with various co-authors, although not one of them became particularly noteworthy. Most of them continued his early research, or tried to apply traditional methods of mathematical physics to various complex phenomena similar to fluid flow.



Mitchell liked interacting with the upper echelons of academia. He received all sorts of awards and recognition (except for the Nobel Prize). But until the end he considered himself an outsider - a Renaissance man who focused on physics, but did not fully believe in all institutions and practices.



Since the early 1980s, I have seen quite regularly with Mitchell, in New York and elsewhere. He used the Mathematica platform daily, praised it, and often talked about the complex calculations that he performed with it. Like many mathematical physicists, Mitchell was an expert on special functions, and often talked with me about more and more exotic functions, which, in his opinion, we should add to the product.



Mitchell had two major hobbies outside the academic field. In the mid-1980s, the young poetess, who is now called Katie Hammond, and whom Mitchell knew from Cornell, was an advertising manager for the New York Times, and married a man from a family that owned the Hammond World Atlas Publishing House. Through it, Mitchell plunged into a completely new world of cartography.



I talked with him on this topic many times. He was proud to come up with how to use the Riemann map theorem to obtain special local mappings when creating maps. He described to me a physics-based algorithm for placing labels on maps (although I still did not understand him completely). He was very pleased with the release of the new edition of Hammond's atlas (which he later called "my atlas").



Since the 1980s, the trend of applying physical ideas to quantitative finance has been actively developing, and physicists often become Wall Street analysts. And since financiers are constantly looking for unique benefits, there is always interest in new methods. I was often contacted with such questions - but after the success of James Gleick's 1987 book “Chaos” (about which I gave a long interview), a whole crowd of people appeared who wanted to know how “chaos” could help them manage their finances.



One of them was someone Michael Gudkin . Studying in college in the early 1960s, He founded a law research company for law students. A few years later, he hired several economists who won the Nobel Prize, and founded, perhaps, the first hedge fund to deal with arbitrage trading using computers. Gudkin was a moto all his life, he loved gambling, travel and backgammon, and earned a lot of money. At one of the unfortunate moments, he was looking for some new solution - and discovered the theory of chaos and Mitchell Feigenbaum.



For several years, he worked on various physicists, and then in 1995 he assembled a team and founded the company Numerix to commercialize the use of physical calculation methods in the field of increasingly exotic financial instruments. Mitchell Feigenbaum was the face of the company, although my old friend Nigel Goldenfield and his young colleague Sasha Sokol carried all the hard work.



From the very beginning, the company had a lot of work related to mathematical physics, and Mitchell actively participated in it. He was a great lover of Ito's stochastic calculus, lectured on it and was proud to have found a method of accelerating stochastic integration a thousandfold. However, the company actually wrote libraries in C ++ for integration into bank systems. Mitchell did not want to do something like this in the long run. After several years of work, his activity in the company decreased.



I met with Gudkin in 1998, and then 14 years later. Shortly before that, he wrote an autobiography, “The Wrong Answer to Get Faster: A Confidential History of Creating a Trillion-Trading Machine,” and suddenly got in touch with me, inviting me to participate in a new obscure business. Mitchell still spoke well of Michael, although when the conversation suddenly went that I founded a new company and became its director, I refused.



All these years, I quite often talked with Mitchell, although our contacts were not as well preserved in the archive as they could be, because he liked talking more by voice than by mail. He wrote to me once: “I do not like to correspond by email. I still prefer to hear the voice and interact with the person. "



But some fragments were preserved in my archive. There is, for example, correspondence regarding Mitchell’s 60th birthday in 2004, which I didn’t get to, because it intersected with the birthday of one of my children. Instead, I ordered the production of the Feigenbaum-Zvitanovich Crystal, a three-dimensional glass sculpture depicting the restriction of the function g (z) on the complex plane.



Solving the functional equation was a little difficult, and laser engraving first split a couple of glass blocks, but in the end I managed to fabricate and send this object - and many years later I was pleased to see it on a shelf in Mitchell’s apartment:







Sometimes, in my archives, mentions of Mitchell pop up by other people, usually by the Predrag. In 2007, Predrag wrote to me (with his characteristic sense of humor):



To other news: just met Mitchell, he meets with Odyssey.



I do not mean an expensive escort service, but Homer's Odyssey. He set about calculating the location of stars as a function with a 26,000 year precession. He says that Hipparchus once calculated all this, but the Catholic Church managed to destroy all copies of his tablets. "



Justifying his image as a Renaissance man, Mitchell was always seriously interested in history. In 2013, in response to my article on Leibniz, Mitchell said that he had been a Leibniz lover since adolescence, and explained:



“Newton’s hagiographer , Voltaire, had no idea about the essence of monadology , so I could only fake“ the best of all possible worlds. ”Once upon a time I published this as an oral means of explaining the universality of 2 ⁿ .



The second of Leibniz’s works, published when he was 19, “On Tangent Inversion Methods,” or something like that, contained the invention of the isocline method for solving ordinary differential equations. Leibniz and Newton start with differential equations, having already received differential notation. Very interesting story".



However, mathematical physics has always been a stronghold of Mitchell’s intellectual life, although more personally, than as part of his academic work. At some point, his goddaughter, being very young, asked him why the moon, being closer to the horizon, seems to be larger. He wrote her an answer (a bit like Euler’s letters to a German princess), and then realized that he was not sure of the answer, and embarked on many years of research in optics and imaging. Once at MIT, he became interested in the work of the retina, inspired by Jerry Lettwin’s book “What the Frog’s Eye Says to the Frog’s Brain”.



He told me about this, saying that the usual theory of image formation is wrong, and that he has a better theory. He always used the size of the moon as an example, but I was not sure whether this problem was related to optics or perception. He never published works related to this topic, although with some luck his manuscripts (according to rumors, he was preparing a book), they will eventually see the light - if anyone else can understand them.



When I visited Mitchell and Gunilla, their apartments made a bohemian impression - everywhere there were books, papers, paintings, and various similar things. And there was a Bird. It was a cockatoo, and it was loud. I don’t know who and why brought it. But he was pretty troublesome. Mitchell and Gunilla were nearly kicked out of the apartment due to neighbors' complaints of noise, and they eventually drove the Bird to the doctors. As I later found out, unexpectedly reviewing the never-implemented plan for developing video games for pets (“someone else’s mind on our planet”), cockatoos are social creatures, and such pets definitely need “Twitter for cockatoos”.







As a result, Gunilla left the family, and, according to rumors, it was because of the Bird.



The last time we met with Mitchell in person a few years ago. My son Christopher and I came to visit him - and he was Mitchell-like excited, his eyes sparkled, he spoke quickly and a little mysteriously on the subject of mathematical physics of image formation. “The eyes of the birds are overrated,” he said to the sound of his cockatoo from the next room. Their central fossa is very small. Their eyes work like telescopes. ”



“The eyes of fish are best,” he said, explaining that all eyes appeared as a result of evolution underwater, and since then their architecture has not changed much. “Fish keep the entire field of view in focus, unlike us,” he said. It was charming, eccentric and very Mitchell.



For years, we periodically talked on the phone, usually late in the evening. A few months ago I met Predrag, and told him that I was surprised that I had not spoken to Mitchell for a long time. He explained that Mitchell was ill, but did not tell anyone about it. A few weeks ago, around midnight, Predrag sent me an email with the subject “Mitchell is dead,” explaining that Mitchell died at around 8 p.m. and attached a typical photograph of “Mitchell in New York” to the letter:







Over the years, I have developed a certain ritual for myself - when I hear about the death of a friend, I immediately start looking for him in my archives. And I suddenly discovered that a few years ago Mitchell phoned my voicemail, the existence of which I did not even suspect. So now I can give Mitchell the opportunity to say the last word .



And, of course, write the last number: 4.66920160910299067185320382 ...