Cosmology and quantum fluctuations in the browser

Let us set a purely practical goal - to realize an endless canvas with the ability to move and scale it with the mouse. Such a canvas, for example, can serve as a moving coordinate system in a graphical editor. The implementation of our idea is not so complicated, but the process of understanding it is associated with fundamental mathematical and physical objects, which we will consider as we develop.

Result

Formulation of the problem

From our canvas, we want to perform only two functions: moving the mouse and the movement of the mouse, as well as zooming when scrolling. The arena of our transformations will choose a browser. Weapons, in this case, do not have to choose.

State machine

The behavior of such systems is conveniently described by transitions between their states, i.e. state machine $$$\ delta: S \ rightarrow S$ where $$$\ delta$ - the transition function between states, displaying many states in itself.

In our case, the state diagram looks like this:

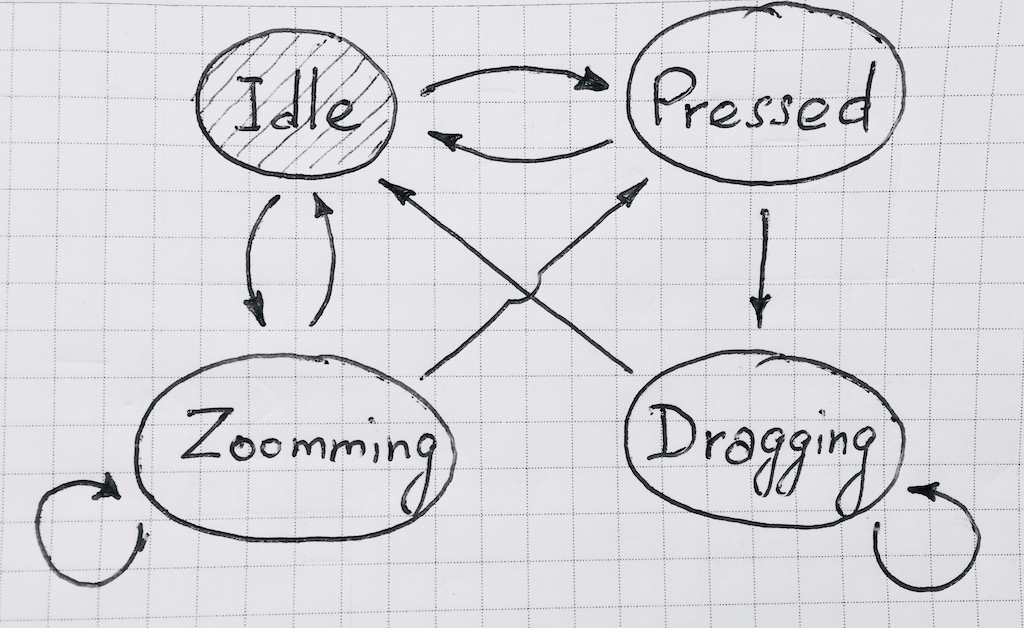
When implementing the transition function, it is convenient to make the event-dependent. This will become apparent in the future. Similarly, it is convenient to be able to subscribe to a change in the state of the machine.

type State = string | number; type Transition<States = State> = { to: States, where: (event: Event) => Array<boolean>, }; type Scheme<States = State> = { [key: States]: Array<Transition<States>> }; interface FSM<States = State> { constructor(state: States, scheme: Scheme<States>): void; // Returns true if the scheme had a transition, false otherwise get isActive(): boolean; // Dispatch event and try to do transition dispatch(event: Event): void; // subscribe on state change on(state: States, cb: (event: Event) => any): FSM<States>; // remove subscriber removeListener(state: States, cb: (event: Event) => any): void; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

We postpone the implementation for a while and take up the geometric transformations that underlie our task.

Geometries

If the issue with moving the canvas is so obvious that we will not dwell on it, then stretching should be considered in more detail. First of all, we require that the stretch leaves one single point stationary - the mouse cursor. The reversibility condition must also be satisfied, i.e. the reverse sequence of user actions should bring the canvas to its original position. What geometry is suitable for this? We will consider some group of point transformations of the plane into itself $$$\ mathbb {R} ^ 2 \ rightarrow \ mathbb {R} ^ 2$ , which is generally expressed by the introduction of new variables $$$x ', y'$ defined as functions of old:

$$

$$x '= \ varphi (x, y) \\ y' = \ psi (x, y)$$

In accordance with the principle of duality in mathematics, such transformations can be interpreted as a change in the coordinate system, as well as a transformation of the space itself with the latter fixed. The second interpretation is convenient for our purposes.

A modern understanding of geometry is different from an understanding of the ancients. According to F. Klein , - geometry studies invariants with respect to certain transformation groups. So, in a group of movements $$$D$ the invariant is the distance between two points $$$d ((x_ {1}, y_ {1}), ((x_ {2}, y_ {2})) = \ sqrt {(x_ {1} - x_ {2}) ^ 2+ (y_ {1 } - y_ {2}) ^ 2}$ . It includes parallel transfers $$$T _ {(x, y)}$ on vector $$$(x, y)$ rotation $$$R _ {\ phi}$ relative to the origin at an angle $$$\ phi$ and reflections $$$M_ {l}$ relative to some line $$$l$ . Such movements are called elementary. The composition of the two movements belongs to our group and sometimes comes down to elementary. So, for example, two consecutive mirror reflections relative to straight lines $$$l$ and $$$n$ give a rotation around a certain center at a certain angle (check for yourself):

$$

$$M_ {l} \ circ M_ {n} = T _ {(- a, -b)} \ circ R _ {\ alpha} \ circ T _ {(a, b)}$$

Surely you already guessed that such a group of movements $$$D$ forms Euclidean geometry. However, stretching does not preserve the distance between two points, but their relationship. Therefore, a group of movements, although it should be included in our scheme, but only as a subgroup.

The geometry that suits us is based on a stretch group $$$P$ to which, in addition to the above movements, homothety is added $$$S_ {k}$ by coefficient $$$k$ .

Well, the last. The reverse element must be present in the group. And therefore there is a neutral $$$e$ (or single) that does not change anything. for example

$$

$$S_ {k} \ circ S_ {k} ^ {- 1} = e$$

means first stretching in $$$k$ times and then in $$$1 / k$ .

Now we can describe the stretching, leaving the mouse cursor point fixed, in group-theoretical language:

$$

$$(x, y) \ rightarrow (x, y) (T _ {(- clientX, -clientY)} \ circ S_ {k} \ circ T _ {(clientX, clientY)})$$

Express the movement $$$T _ {(x, y)}$ and $$$S_ {k}$ and their composition as functions of a vector in code

 type Scalar = number; type Vec = [number, number]; type Action<A = Vec | Scalar> = (z: Vec) => (v: A) => Vec; // Translate const T: Action<Vec> = (z: Vec) => (d: Vec): Vec => [ z[0] + d[0], z[1] + d[1] ]; // Scale const S: Action<Scalar> = (z: Vec) => (k: Scalar): Vec => [ z[0] * k, z[1] * k ]; const compose = (z: Vec) => (...actions: Array<(z: Vec) => Vec>) => actions.reduce((z, g) => g(z), z);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Note that so far we have been working with a group of continuous transformations. However, the computer does not work with continuous quantities, therefore, following Poincare, we will understand a continuous group as an infinite group of discrete operations. Now that we have figured out the geometry, we should turn to the relativity of motion.

Cosmology of the canvas. Modular grid

For a century, as humanity, the expansion of the universe has been known. Observing distant objects - galaxies and quasars, we register the shift of the electromagnetic spectrum towards longer waves - the so-called cosmological redshift. Any measurement connects the observer, the observed and the means of measurement in relation to which we make our measurements. Without measuring instruments, it is impossible to establish invariant relations in nature, i.e., to determine the geometry of the Universe. However, geometry loses its meaning without observability. So in our task it’s nice to have landmarks, like galaxies, in relation to the light of which we can determine the relativity of the movement of our canvas. Such a structure can be a periodic lattice, which bifurcates each time when the space is expanded twice.

Since the lattice is periodic, it is convenient to adopt a modular algebra. Thus, we will act as a group $$$P$ also on the torus $$$T ^ 2 = S ^ 1 \ times S ^ 1$ . Since the monitor screen is not a continuous plane, but an integer lattice $$$\ mathbb {Z} ^ 2$ (we neglect now that it is finite), then the action of the group $$$P$ must be considered on an integer torus $$$\ mathbb {Z} _ {p} ^ 2$ where $$$p$ - the size of the edge of the square $$$p \ times p$ :

Thus, once and for all fixing our torus near the origin, we will perform all further calculations on it. Then propagate it using standard canvas library methods. Here's what a one pixel move looks like:

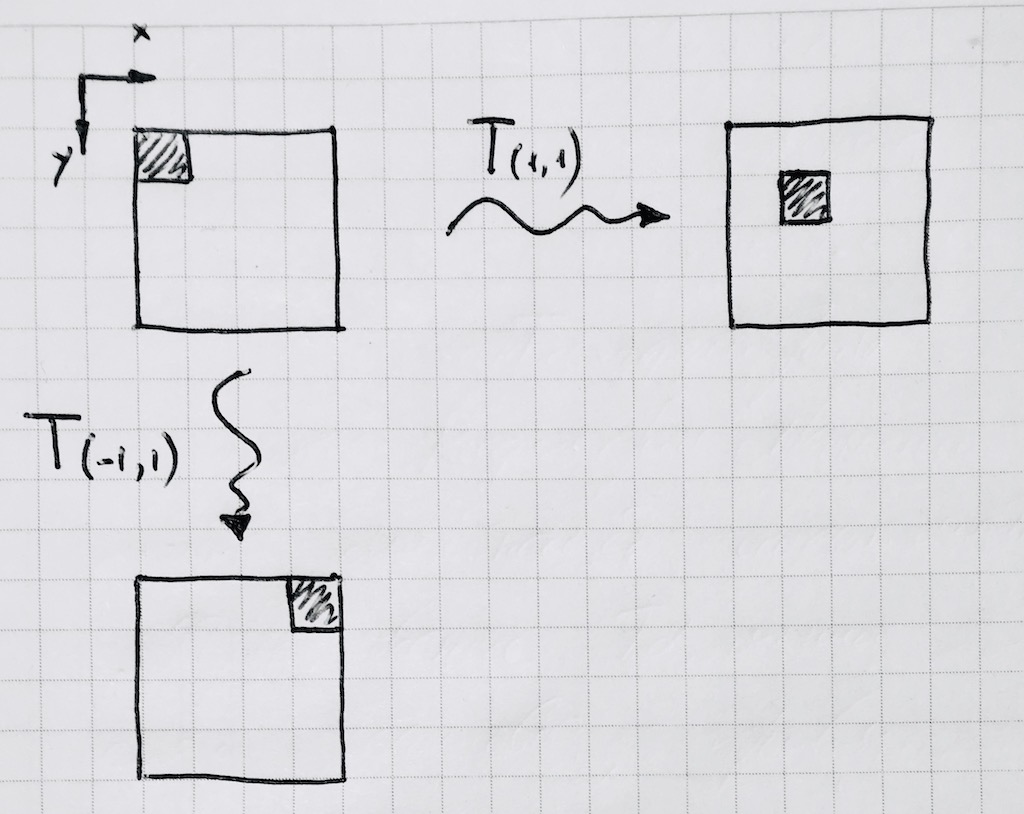
Obviously, the standard operation of taking the module x% p is not suitable for us, since it translates negative values ​​of the argument into negative ones, but there are none on the integer torus. Write your function $$$x \ mod p$ :

 const mod = (x, p) => x >= 0 ? Math.round(x) % p : p + Math.round(x) % p;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Now back to the final state machine and

Next, define a transition scheme, create a canvas and

Then you should determine the rendering function, set the necessary initial values ​​and subscribe to the change of state. Consider the most interesting part of the code:

  fsm.on('zooming', (event: WheelEvent) => { // next scale factor const nk = g >= 1 ? round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e2) : round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e12); // gain g = 2 ** Math.trunc(Math.log2(nk)); if (g < min || g > max) return; vec = compose(vec)( T([-event.clientX, -event.clientY]), S(nk / k), T([event.clientX, event.clientY]) ); size = base * nk; patternCanvas.width = Math.round(size / g); patternCanvas.height = Math.round(size / g); xyMod = [ mod(vec[0], patternCanvas.width), mod(vec[1], patternCanvas.height) ]; k = nk; main(); });
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Firstly, we are expanding not by the coefficient k, but by some ratio nk / k. This is due to the fact that the m-step of our mapping at a fixed point $$$(a, b)$ expressed as

$$

$$x_ {m} = (x_ {m-1} -a) k_ {m-1} ^ * + a \\ y_ {m} = (y_ {m-1} -b) k_ {m-1} ^ * + b$$

or, relative to the initial values $$$x_ {1}, y_ {1}$

$$

$$x_ {m} = (x_ {1} -a) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + a \\ y_ {m} = (y_ {1} -b) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + b$$

Obviously the product $$$\ prod_ {i = 1} ^ {m-1} k_ {i} ^ *$ there is a nonlinear function of the iteration step and either very quickly converges to zero, or runs away to infinity with small initial deviations.

We introduce the variable g, which is a measure of doubling our canvas. Obviously, it takes on a constant value on a certain interval. To achieve linearity $$$k_ {i} ^ *$ use homogeneous substitution

$$

$$k_ {i + 1} ^ * = \ frac {k_ {i + 1}} {k_ {i}}, k_ {1} = 1$$

Then all the members in the work, except the first and last, will be reduced:

$$

$$\ prod_ {i = 1} ^ {m-1} k_ {i} ^ * = \ prod_ {i = 1} ^ {m-1} \ frac {k_ {i}} {k_ {i-1}} = \ frac {k_ {2}} {1} \ frac {k_ {3}} {k_ {2}} ... \ frac {k_ {m-2}} {k_ {m-3}} \ frac { k_ {m-1}} {k_ {m-2}} = k_ {m-1}$$

Further, the phase jump g reduces the expansion rate in such a way that the fractal structure that unfolds before us always moves linearly. Thus, we obtain an approximated variation of the Hubble power law of the expansion of the Universe.

It remains to understand the limits of accuracy of our model.

Quantum fluctuations. 2-adic number field

Understanding the measurement process led to the concept of a real number. Heisenberg's uncertainty principle points to its limits. A modern computer does not work with real numbers, but with machine words, the length of which is determined by the capacity of the processor. Machine words form a field of 2-adic numbers $$$\ mathbb {Q_ {2}}$ and are denoted as $$$\ mathbb {F_ {2} ^ {n}}$ where $$$n$ - word length. The measurement process in this case is replaced by the calculation process and is associated with a non-Archimedean metric:

$$

$$\ forall n \ in \ mathbb {Z}, z \ in \ mathbb {F_ {2} ^ {n}}: n \ cdot z <2 ^ n$$

Thus, our model has a limit of computation. Limitations are described in the IEEE_754 standard. Starting at some point, our base size will go beyond the limit of accuracy and the operation of taking the module will begin to generate errors resembling pseudo-random sequences. This is simply verified by deleting the line

 if (g < min || g > max) return;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

The final limit in our case is calculated by the semi-empirical method, since we work with several parameters.

Conclusion

Thus, seemingly distant at first glance, theories are connected on the canvas in the browser. The concepts of action, measurement and calculation are closely related to each other. The issue of combining them is still not resolved.

Result