Amount Problem
In the famous task with coins, which need to count the change, as you know, there are two troubles .
- the first is the number of denominations of coins,
- the second is the number of digits of the number representing the change.
And both of these quantities have an exponential effect on the load of the Turing machine, which is actually involved in the calculation.
Recognizing that a person has two dependencies at once is not accepted even in the society of alcoholics. Therefore, I decided to play it safe and get rid of one of these problems in advance. The way this will be the number of denominations of coins.
In a nutshell, the essence of the problem is described as follows: exponential dependence. That is, the release of a new type of coins of a hitherto denomination denomination entails an increase in the number of combinations of coins in half. Another denomination - twice as much, and so on to conditional infinity. With galloping inflation, when new coins / bills are issued often enough, you will have to buy a more powerful computer to solve the problem. And where to get the money for it at a galloping inflation?
So, a solution that is actually quite simple.
If you imagine a segment from zero to C (change) with the points on it corresponding to the denominations of coins, then any intelligent person will see approximately the following picture:

Well, maybe in different colors.
So what can we say about red dots? Of course, the fact that the number corresponding to any of this point is the amount that we can give out in the form of change. And with one coin. Maybe someone saw something else, but I, as an artist, invested precisely this meaning. And, as an artist, I’ll draw another point in this picture that corresponds to the sum of the first (from left to right) point with the same point (everything is correct: it will double the face value). I draw in the same color, for a new dot means the same thing - this amount can also be a change.
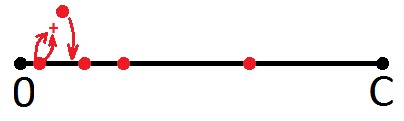
Next, I take the first point and summarize with the second, even if the second point is the previous sum (this does not matter, because all points are equal here). I’ll put a new point on the segment again.
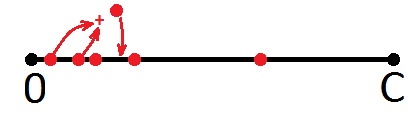
If the new point goes beyond the bounds of the segment, then we do not draw anything, but return to the beginning of the segment and take the next point, that is, the second. Further the same (from left to right).
Actually, when point C (I remind you, this is change) turns red, we can assume that a solution has been found. And you can go through the full cycle and find the optimal solution, so that the number of coins is minimal.
From a programming point of view, there are two cycles. The first is from 0 to C / 2 (there is no need to take the first point of greater C / 2, since the second point is always larger than the first and in total they will go beyond the boundaries of the segment). The second cycle is built into the first, it starts from the same point that the external cycle points to and until the sum leaves the boundary of the segment.
In fact, this is a bust: we do not lose a single option, and we are guaranteed to find the optimal solution, or we will conclude that there is no solution.
Let's count the amount of iteration inside our loops. In the external cycle - this is C / 2, in the internal - somewhere the same. Multiply C / 2 * C / 2 = (C ^ 2) / 4. Round to C squared. This is the worst option when our entire segment simply consists of red dots. If there are spaces between the points, the number of iterations will decrease significantly.
As you can see, when determining the difficulty of solving the problem, we do not use the number of coin denominations. This value does not directly affect the complexity of the solution. The values of these denominations affect, say a 1 cent coin and make this segment completely red. Therefore, it is better not to take this coin into account, and at the end of the decision, take the red point closest to C and sketch on top of one-cent. But this is already the moment of optimization of the algorithm, and it is beyond the scope of this article.
That's all that I would like to say. A working version of the program can be found here: github link
1. In the init.h file, set COINS_NUMBER - the number of denominations of coins, and AMOUNT - the amount of change.
2. In the file coinc.c specify the denominations of coins in the coins array.
3. Under Linux, run make_sh.
4. Run the app program for execution
Let me give you some funny example . Imagine that in some country mathematicians came to power and put into circulation 32 denominations of coins: 2, 3, 5, 7, 11, 13, 17, 19 ... 131. For the convenience of counting, only prime numbers were chosen (well, isn’t it funny ?). And in order to make sure that the monetary reform was successful, they sent a messenger in the store to exchange bill 5333 (also a prime number). The cashier on an old single-core solution solved the problem: 39 coins with a face value of 131 Pythagoras, one coin 127 and one 97. The calculation took 3 seconds and a little more than a megabyte of memory. The Government was informed that the people are satisfied with the reform, he believes quickly.
And an example that is a little more difficult to verify. Coins, one hundred denominations in such a strange sequence: 0101, 0202, 0303 ... 9898, 9999, 100100. Amount of change: 101010. The search for a solution took 1 second and a little more than a megabyte of memory. But the decision, in fact, is not, that is, it is impossible to collect such an amount with such coins. With the same coins, a check of 1 million will take 26 megabytes and hundreds of seconds, which indicates an exponential dependence on the amount, but not the number of coin denominations.
- the first is the number of denominations of coins,
- the second is the number of digits of the number representing the change.
And both of these quantities have an exponential effect on the load of the Turing machine, which is actually involved in the calculation.
Recognizing that a person has two dependencies at once is not accepted even in the society of alcoholics. Therefore, I decided to play it safe and get rid of one of these problems in advance. The way this will be the number of denominations of coins.
In a nutshell, the essence of the problem is described as follows: exponential dependence. That is, the release of a new type of coins of a hitherto denomination denomination entails an increase in the number of combinations of coins in half. Another denomination - twice as much, and so on to conditional infinity. With galloping inflation, when new coins / bills are issued often enough, you will have to buy a more powerful computer to solve the problem. And where to get the money for it at a galloping inflation?
So, a solution that is actually quite simple.
If you imagine a segment from zero to C (change) with the points on it corresponding to the denominations of coins, then any intelligent person will see approximately the following picture:

Well, maybe in different colors.
So what can we say about red dots? Of course, the fact that the number corresponding to any of this point is the amount that we can give out in the form of change. And with one coin. Maybe someone saw something else, but I, as an artist, invested precisely this meaning. And, as an artist, I’ll draw another point in this picture that corresponds to the sum of the first (from left to right) point with the same point (everything is correct: it will double the face value). I draw in the same color, for a new dot means the same thing - this amount can also be a change.

Next, I take the first point and summarize with the second, even if the second point is the previous sum (this does not matter, because all points are equal here). I’ll put a new point on the segment again.

If the new point goes beyond the bounds of the segment, then we do not draw anything, but return to the beginning of the segment and take the next point, that is, the second. Further the same (from left to right).
Actually, when point C (I remind you, this is change) turns red, we can assume that a solution has been found. And you can go through the full cycle and find the optimal solution, so that the number of coins is minimal.
From a programming point of view, there are two cycles. The first is from 0 to C / 2 (there is no need to take the first point of greater C / 2, since the second point is always larger than the first and in total they will go beyond the boundaries of the segment). The second cycle is built into the first, it starts from the same point that the external cycle points to and until the sum leaves the boundary of the segment.
In fact, this is a bust: we do not lose a single option, and we are guaranteed to find the optimal solution, or we will conclude that there is no solution.
Let's count the amount of iteration inside our loops. In the external cycle - this is C / 2, in the internal - somewhere the same. Multiply C / 2 * C / 2 = (C ^ 2) / 4. Round to C squared. This is the worst option when our entire segment simply consists of red dots. If there are spaces between the points, the number of iterations will decrease significantly.
As you can see, when determining the difficulty of solving the problem, we do not use the number of coin denominations. This value does not directly affect the complexity of the solution. The values of these denominations affect, say a 1 cent coin and make this segment completely red. Therefore, it is better not to take this coin into account, and at the end of the decision, take the red point closest to C and sketch on top of one-cent. But this is already the moment of optimization of the algorithm, and it is beyond the scope of this article.
That's all that I would like to say. A working version of the program can be found here: github link
1. In the init.h file, set COINS_NUMBER - the number of denominations of coins, and AMOUNT - the amount of change.
2. In the file coinc.c specify the denominations of coins in the coins array.
3. Under Linux, run make_sh.
4. Run the app program for execution
Note
The runtime and the amount of memory used will also be displayed on the screen. I forgot to mention that I have to use additional memory. But its quantity does not depend on the number of denominations, so everything is fair.
Let me give you some funny example . Imagine that in some country mathematicians came to power and put into circulation 32 denominations of coins: 2, 3, 5, 7, 11, 13, 17, 19 ... 131. For the convenience of counting, only prime numbers were chosen (well, isn’t it funny ?). And in order to make sure that the monetary reform was successful, they sent a messenger in the store to exchange bill 5333 (also a prime number). The cashier on an old single-core solution solved the problem: 39 coins with a face value of 131 Pythagoras, one coin 127 and one 97. The calculation took 3 seconds and a little more than a megabyte of memory. The Government was informed that the people are satisfied with the reform, he believes quickly.
Note
PS By the way, having denominations of coins in the form of prime numbers is actually a good idea, because any amount can be represented by two or three coins, and there is no point in big wallets.
And an example that is a little more difficult to verify. Coins, one hundred denominations in such a strange sequence: 0101, 0202, 0303 ... 9898, 9999, 100100. Amount of change: 101010. The search for a solution took 1 second and a little more than a megabyte of memory. But the decision, in fact, is not, that is, it is impossible to collect such an amount with such coins. With the same coins, a check of 1 million will take 26 megabytes and hundreds of seconds, which indicates an exponential dependence on the amount, but not the number of coin denominations.
PS
If it’s interesting, next time I’ll write about how to take a large number, split it into any two / three / ... parts, put these parts into an array, add several hundred random numbers there and, without looking, find the components of the original large numbers.
All Articles