And yet, why Posit are a worthy alternative to IEEE 754
The month of Posit on Habré has been declared open, which means I can’t pass by and ignore the criticism that has fallen on them. In previous series:
A new approach can help us get rid of floating point calculations
Posit-arithmetic: defeating a floating point in his own field. Part 1
Posit-arithmetic: defeating a floating point in his own field. Part 2
Adult Posit Challenges
I think many of you can immediately recall at least one case from history when revolutionary ideas at the time of their formation ran into rejection by a community of experts. As a rule, this behavior is blamed on the vast baggage of already accumulated knowledge, which does not allow looking at the old problem in a new light. Thus, the new idea loses in terms of characteristics to established approaches, because it is evaluated only by those metrics that were considered important at the previous stage of development.
This is precisely the kind of aversion that the Posit format is facing today: critics often simply “look in the wrong direction” and even use the Posit in their experiments in the wrong way. In this article I will try to explain why.
The advantages of Posit have already been said quite a bit: mathematical elegance, high accuracy on low-exponential values, a wide range of values, only one binary representation of NaN and zero, the absence of subnormal values, the fight against overflow / underflow. Critics have been voiced quite a bit: useless accuracy for very large or very small values, a complex binary representation format and, of course, lack of hardware support.
I do not want to repeat the arguments I have already said; instead, I will try to focus on the aspect that, as a rule, is overlooked.
The IEEE 754 standard describes floating point numbers implemented in the Intel 8087 almost 40 years ago. By the standards of our industry, this is an incredible time; everything has changed since then: processor performance, memory cost, data volumes and scale of calculations. The Posit format was developed not just as the best version of IEEE 754, but as an approach to working with numbers that meets the new requirements of the time.
The high-level task has remained the same - we all need effective calculations over the field of rational numbers with minimal loss of accuracy. But the conditions in which the task is being solved are radically changed.
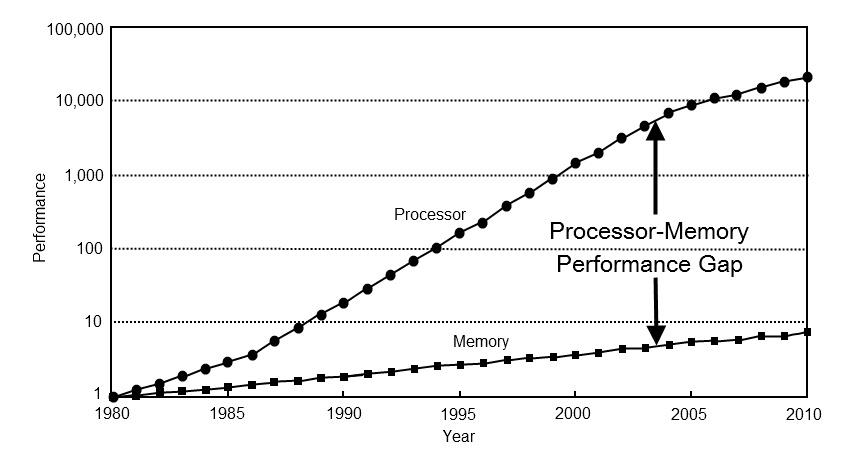
First, the priorities for optimization have changed. 40 years ago, computer performance was almost entirely dependent on processor performance. Today, the performance of most computations rests in memory. To verify this, just look at the key areas of development of processors of the last decades: three-level caching, speculative execution, pipelining of calculations, branch prediction. All these approaches are aimed at achieving high performance in the conditions of fast computing and slow access to memory.
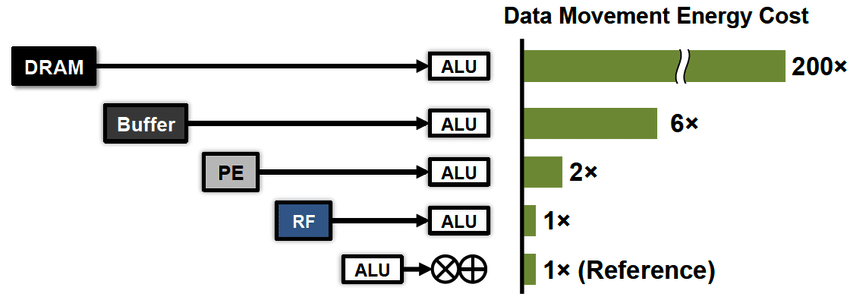
Secondly, a new requirement has come to the fore - effective energy consumption. Over the past decades, the technology of horizontal scaling of computing has advanced so much that we began to care not so much about the speed of these calculations, but about the electricity bill. Here I should emphasize an important part to understand. From the point of view of energy efficiency, calculations are cheap, because the processor registers are very close to its computers. It will be much more expensive to pay for data transfer, both between the processor and the memory (x100), and over long distances (x1000 ...).
Here is just one example of a science project that Posit plans to use:

This network of telescopes generates 200 petabytes of data per second, the processing of which takes the power of a small power plant - 10 megawatts . Obviously, for such projects, the reduction in data and energy consumption is critical.
So what does the Posit standard offer? To understand this, you need to return to the very beginning of the argument and understand what is meant by the precision of floating point numbers.
There are actually two different aspects related to accuracy. The first aspect is the accuracy of the calculations - how much the results of the calculations deviate during various operations. The second aspect is the accuracy of the presentation - how much the original value is distorted at the time of conversion from the field of rational numbers to the field of floating-point numbers of a particular format.
Now there will be an important moment for awareness. Posit is primarily a format for representing rational numbers, not a way to perform operations on them. In other words, Posit is a lossy rational compression format. You may have heard the claim that 32-bit Posit is a good alternative to 64-bit Float. So, we are talking about halving the required amount of data for storing and transmitting the same set of numbers. Two times less memory - almost 2 times less power consumption and high processor performance due to lower expectations of memory access.
Here you should have a logical question: what is the point of efficiently representing rational numbers if it does not allow calculations to be performed with high accuracy.
In fact, there is a way to do exact calculations, and it's called Quire. This is another format for representing rational numbers, inextricably linked with Posit. Unlike Posit, the Quire format is designed specifically for calculations and for storing intermediate values in registers, and not in the main memory.

In short, the Quire is nothing more than a wide integer battery (fixed point arithmetic). The unit, as a binary representation of Quire, corresponds to the minimum positive value of Posit. The maximum Quire value corresponds to the maximum Posit value. Each Posit value has a unique representation in Quire without loss of accuracy, but not every Quire value can be represented in Posit without loss of accuracy.
The benefits of Quire are obvious. They allow you to perform operations with incomparably higher accuracy than Float, and for addition and multiplication operations there will be no loss of accuracy at all. The price you have to pay for this is wide processor registers (32-bit Posit with es = 2 correspond to 512-bit Quire), but this is not a serious problem for modern processors. And if 40 years ago computing over 512 bit integers seemed an unacceptable luxury, today it is rather an adequate alternative to wide access to memory.
Thus, Posit offers not just a new standard in the form of an alternative to Float / Double, but rather a new approach to working with numbers. Unlike Float - which is a single representation trying to find a compromise between accuracy and storage efficiency and computational efficiency, Posit offers two different presentation formats, one for storing and transmitting numbers - Posit itself, and the other for calculations and their intermediate Values - Quire.
When we solve practical problems using floating point numbers, from the point of view of the processor, working with them can be represented as a set of the following actions:
With Float / Double, accuracy is lost in every operation. With Posit + Quire, the loss of accuracy during the calculation is negligible. It is lost only at the last stage, at the time of converting the Quire value to Posit. That is why most of the “error accumulation” problems for Posit + Quire are simply not relevant.
Unlike Float / Double, when using Posit + Quire, we can usually afford a more compact representation of numbers. As a result - faster access to data from memory (better performance) and more efficient storage and transmission of information.
As an illustrative demonstration, I will give just one example - the classical Muller recurrence relation, coined specifically to demonstrate how the accumulation of errors in floating point calculations radically distorts the result of calculations.

In the case of using arithmetic with arbitrary precision, the recurrence sequence should be reduced to the value of 5. In the case of floating point arithmetic, the question is only on which iteration the calculation results will begin to have an inadequately large deviation.
I conducted an experiment for IEEE 754 with single and double precision, as well as for 32-bit Posit + Quire. The calculations were carried out in Quire arithmetic, but each value in the table was converted to Posit.
As you can see from the table, 32-bit Float surrender already at the seventh value, and 64-bit Float lasted until the 14th iteration. At the same time, calculations for Posit using Quire return a stable result up to 58 iterations!
For many practical cases and when used correctly, the Posit format will really allow you to save on memory on the one hand, compressing numbers better than Float does, and on the other hand to provide better calculation accuracy thanks to Quire.
But this is only a theory! When it comes to accuracy or performance, always take tests before blindly trusting one approach or another. Indeed, in practice, your particular case will turn out to be exceptional much more often than in theory.
Well, do not forget Clark's first law (free interpretation): When a respected and experienced expert claims that a new idea will work, he is almost certainly right. When he claims that the new idea will not work, then he is very likely to be mistaken. I do not consider myself an experienced expert to allow you to rely on my opinion, but I ask you to be wary of criticizing even experienced and respected people. After all, the devil is in the details, and even experienced people can miss them.
A new approach can help us get rid of floating point calculations
Posit-arithmetic: defeating a floating point in his own field. Part 1
Posit-arithmetic: defeating a floating point in his own field. Part 2
Adult Posit Challenges
I think many of you can immediately recall at least one case from history when revolutionary ideas at the time of their formation ran into rejection by a community of experts. As a rule, this behavior is blamed on the vast baggage of already accumulated knowledge, which does not allow looking at the old problem in a new light. Thus, the new idea loses in terms of characteristics to established approaches, because it is evaluated only by those metrics that were considered important at the previous stage of development.
This is precisely the kind of aversion that the Posit format is facing today: critics often simply “look in the wrong direction” and even use the Posit in their experiments in the wrong way. In this article I will try to explain why.
The advantages of Posit have already been said quite a bit: mathematical elegance, high accuracy on low-exponential values, a wide range of values, only one binary representation of NaN and zero, the absence of subnormal values, the fight against overflow / underflow. Critics have been voiced quite a bit: useless accuracy for very large or very small values, a complex binary representation format and, of course, lack of hardware support.
I do not want to repeat the arguments I have already said; instead, I will try to focus on the aspect that, as a rule, is overlooked.
Game rules have changed
The IEEE 754 standard describes floating point numbers implemented in the Intel 8087 almost 40 years ago. By the standards of our industry, this is an incredible time; everything has changed since then: processor performance, memory cost, data volumes and scale of calculations. The Posit format was developed not just as the best version of IEEE 754, but as an approach to working with numbers that meets the new requirements of the time.
The high-level task has remained the same - we all need effective calculations over the field of rational numbers with minimal loss of accuracy. But the conditions in which the task is being solved are radically changed.
First, the priorities for optimization have changed. 40 years ago, computer performance was almost entirely dependent on processor performance. Today, the performance of most computations rests in memory. To verify this, just look at the key areas of development of processors of the last decades: three-level caching, speculative execution, pipelining of calculations, branch prediction. All these approaches are aimed at achieving high performance in the conditions of fast computing and slow access to memory.

Secondly, a new requirement has come to the fore - effective energy consumption. Over the past decades, the technology of horizontal scaling of computing has advanced so much that we began to care not so much about the speed of these calculations, but about the electricity bill. Here I should emphasize an important part to understand. From the point of view of energy efficiency, calculations are cheap, because the processor registers are very close to its computers. It will be much more expensive to pay for data transfer, both between the processor and the memory (x100), and over long distances (x1000 ...).

Here is just one example of a science project that Posit plans to use:

This network of telescopes generates 200 petabytes of data per second, the processing of which takes the power of a small power plant - 10 megawatts . Obviously, for such projects, the reduction in data and energy consumption is critical.
To the very beginning
So what does the Posit standard offer? To understand this, you need to return to the very beginning of the argument and understand what is meant by the precision of floating point numbers.
There are actually two different aspects related to accuracy. The first aspect is the accuracy of the calculations - how much the results of the calculations deviate during various operations. The second aspect is the accuracy of the presentation - how much the original value is distorted at the time of conversion from the field of rational numbers to the field of floating-point numbers of a particular format.
Now there will be an important moment for awareness. Posit is primarily a format for representing rational numbers, not a way to perform operations on them. In other words, Posit is a lossy rational compression format. You may have heard the claim that 32-bit Posit is a good alternative to 64-bit Float. So, we are talking about halving the required amount of data for storing and transmitting the same set of numbers. Two times less memory - almost 2 times less power consumption and high processor performance due to lower expectations of memory access.
Second end of the stick
Here you should have a logical question: what is the point of efficiently representing rational numbers if it does not allow calculations to be performed with high accuracy.
In fact, there is a way to do exact calculations, and it's called Quire. This is another format for representing rational numbers, inextricably linked with Posit. Unlike Posit, the Quire format is designed specifically for calculations and for storing intermediate values in registers, and not in the main memory.

In short, the Quire is nothing more than a wide integer battery (fixed point arithmetic). The unit, as a binary representation of Quire, corresponds to the minimum positive value of Posit. The maximum Quire value corresponds to the maximum Posit value. Each Posit value has a unique representation in Quire without loss of accuracy, but not every Quire value can be represented in Posit without loss of accuracy.
The benefits of Quire are obvious. They allow you to perform operations with incomparably higher accuracy than Float, and for addition and multiplication operations there will be no loss of accuracy at all. The price you have to pay for this is wide processor registers (32-bit Posit with es = 2 correspond to 512-bit Quire), but this is not a serious problem for modern processors. And if 40 years ago computing over 512 bit integers seemed an unacceptable luxury, today it is rather an adequate alternative to wide access to memory.
Putting the puzzle together
Thus, Posit offers not just a new standard in the form of an alternative to Float / Double, but rather a new approach to working with numbers. Unlike Float - which is a single representation trying to find a compromise between accuracy and storage efficiency and computational efficiency, Posit offers two different presentation formats, one for storing and transmitting numbers - Posit itself, and the other for calculations and their intermediate Values - Quire.
When we solve practical problems using floating point numbers, from the point of view of the processor, working with them can be represented as a set of the following actions:
- Read the values of numbers from memory.
- Perform some sequence of operations. Sometimes the number of operations is quite large. In this case, all intermediate values of the calculations are stored in registers.
- Write the result of operations to memory.
With Float / Double, accuracy is lost in every operation. With Posit + Quire, the loss of accuracy during the calculation is negligible. It is lost only at the last stage, at the time of converting the Quire value to Posit. That is why most of the “error accumulation” problems for Posit + Quire are simply not relevant.
Unlike Float / Double, when using Posit + Quire, we can usually afford a more compact representation of numbers. As a result - faster access to data from memory (better performance) and more efficient storage and transmission of information.
Mueller Ratio
As an illustrative demonstration, I will give just one example - the classical Muller recurrence relation, coined specifically to demonstrate how the accumulation of errors in floating point calculations radically distorts the result of calculations.

In the case of using arithmetic with arbitrary precision, the recurrence sequence should be reduced to the value of 5. In the case of floating point arithmetic, the question is only on which iteration the calculation results will begin to have an inadequately large deviation.
I conducted an experiment for IEEE 754 with single and double precision, as well as for 32-bit Posit + Quire. The calculations were carried out in Quire arithmetic, but each value in the table was converted to Posit.
Experiment Results
# float (32) double (64) posit (32) ------------------------------------- ----------- 0 4.000000 4.000000 4.250000 4 1 4.250000 4.25 2 4.470589 4.470588 4.470588237047195 3 4.644745 4.644737 4.644736856222153 4 4.770706 4.770538 4.770538240671158 5 4.859215 4.855701 4.855700701475143 6 4.983124 4.910847 4.91084748506546 7 6.395432 4.945537 4.94553741812706 8 27.632629 4.966962 4.966962575912476 9 86.993759 4.980042 4.980045706033707 10 99.255508 4.987909 4.98797944188118 11 99.962585 4.991363 4.992770284414291 12 99.998131 4.967455 4.99565589427948 13 99.999908 4.429690 4.997391253709793 14 100.000000 -7.817237 4.998433947563171 15 100.000000 168.939168 4.9990600645542145 16 100.000000 102.039963 4.999435931444168 17 100.000000 100.099948 4.999661535024643 18 100.000000 100.004992 4.999796897172928 19 100.000000 100.000250 4.999878138303757 20 100.000000 100.000012 4.999926865100861 21 100.000000 100.000001 4.999956130981445 22 100.000000 100.000000 4.999973684549332 23 100.000000 100.0000 00 4.9999842047691345 24 100.000000 100.000000 4.999990522861481 25 100.000000 100.000000 4.999994307756424 26 100.000000 100.000000 4.999996602535248 27 100.000000 100.000000 4.999997943639755 28 100.000000 100.000000 4.999998778104782 29 100.000000 100.000000 4.99999925494194 30 100.000000 100.000000 4.999999552965164 31 100.000000 100.000000 4.9999997317790985 32 100.000000 100.000000 4.999999850988388 33 100.000000 100.000000 4.999999910593033 34 100.000000 100.000000 4.999999940395355 35 100.000000 100.000000 4.999999970197678 36 100.000000 100.000000 4.999999970197678 37 100.000000 100.000000 5 38 100.000000 100.000000 5 39 100.000000 100.000000 5 40 100.000000 100.000000 5 41 100.000000 100.000000 5 42 100.000000 100.000000 5 43 100.000000 100.000000 5 44 100.000000 100.000000 5 45 100.000000 100.000000 5 46 100.000000 100.000000 50000 5.000000 50000 470 100.000000 5 49 100.000000 100.000000 5 50 100.000000 100.000000 5 51 100.000000 100.000000 5 52 100.000000 100.000000 5.000000059604645 53 100.000000 100.000000 5.000000983476639 54 100.000000 100.000000 5.000019758939743 55 100.000000 100.000000 5.000394910573959 56 100.000000 100.000000 5.007897764444351 57 100.000000 100.000000 5.157705932855606 58 100.000000 100.000000 8.057676136493683 59 100.000000 100.000000 42.94736957550049 60 100.000000 100.000000 93.35784339904785 61 100.000000 100.000000 99.64426326751709 62 100.000000 100.000000 99.98215007781982 63 100.000000 100.000000 99.99910736083984 64 100.000000 100.000000 99.99995517730713 65 100.000000 100.000000 99.99999809265137 66 100.000000 100.000000 100 67 100.000000 100.000000 100 68 100.000000 100.000000 100 69 100.000000 100.000000 100 70 100.000000 100.000000 100
As you can see from the table, 32-bit Float surrender already at the seventh value, and 64-bit Float lasted until the 14th iteration. At the same time, calculations for Posit using Quire return a stable result up to 58 iterations!
Morality
For many practical cases and when used correctly, the Posit format will really allow you to save on memory on the one hand, compressing numbers better than Float does, and on the other hand to provide better calculation accuracy thanks to Quire.
But this is only a theory! When it comes to accuracy or performance, always take tests before blindly trusting one approach or another. Indeed, in practice, your particular case will turn out to be exceptional much more often than in theory.
Well, do not forget Clark's first law (free interpretation): When a respected and experienced expert claims that a new idea will work, he is almost certainly right. When he claims that the new idea will not work, then he is very likely to be mistaken. I do not consider myself an experienced expert to allow you to rely on my opinion, but I ask you to be wary of criticizing even experienced and respected people. After all, the devil is in the details, and even experienced people can miss them.
All Articles