この投稿では、網膜のレベルでさえも発生する人間の知覚の特徴のいくつかについて語っています（脳内の画像の分析前）。 太字は、投稿のトピックに直接関連する瞬間を強調しています。 明確でない用語がある場合は、 最初の部分を参照してください。
色知覚の特徴
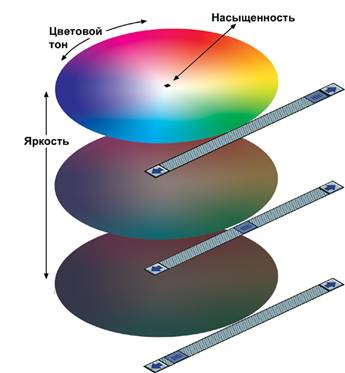
主な色パラメータは、色調、明るさ、彩度であり、反射光の物理パラメータの複雑さに対応します：波長、強度、スペクトル純度。
明るさ。 強度が高いほど、色がより鮮明に表示されます。 ただし、同じ強度では、一部の色はより明るく見えます（たとえば、黄色と青）。 これは、異なるタイプのコーンの数とそれらが知覚する色のタイプの分布によるものです（たとえば、黄色は2つのタイプのコーンによってすぐに知覚され、青よりもはるかに強くなります）。
スペクトル的に純粋な単色光は可能な限り飽和しますが、単色光に異なる波長または白色の光を追加すると、色は純粋ではなく、明るいと認識されます。
3次元カラースピンドルダイアグラムは、色調、明るさ、彩度の関係を示しています（ハーベイシフマンの著書 「Feelings and Perceptions」からの図解）。
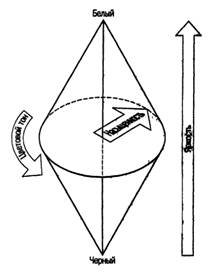
スピンドル軸はすべての灰色の濃淡を表し、知覚される彩度の感覚はディスクによって示され、その中心から端に向かって増加します。
この図は、彩度が中程度の輝度レベルでのみ最大になり、輝度が増加または減少すると、飽和感が減少することを明確に示しています。
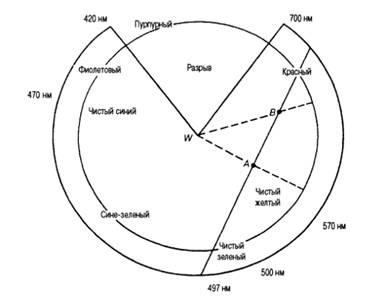
ニュートンのカラーホイールは、最大彩度レベルのスピンドルの中央ディスクに対応しています。 色の知覚におけるいくつかのパターンを強調するために、色はカラーホイールに配置されます。
各色には独自の補色があり、カラーホイールの正反対の位置を占めます。 特定の比率で取られた補色の混合物は、白色または灰色を形成します。 補色のペアは、視覚システムに対する互いの影響を相殺するため、拮抗色です。
補色の例：青と黄色、赤と青緑、緑とマゼンタ、およびマゼンタはカラーホイールの外側にありますが、これは独自のカラーウェーブを持たないためですが、スペクトル的に純粋な色が混ざったときに生じる感覚です。
同じ感覚を引き起こすが、物理的性質が異なる色はメタマーと呼ばれます。 メタマーの例は、プリズムを介して白色光を分解することによって得られるスペクトルの緑と、黄色と青のインクを混合することによって得られる緑です。 色は加法および減法です。 ここで色がどのように書かれているかについて良いです 、そして、色モデルは絵の知覚についての会話の範囲内に完全にないので、上の色は十分です。 これは、人間の目によるモニター上のピクセルのグループの認識を完全に説明します。
網膜機能
多くの実験が行われた結果、人は境界だけで色と照明の変化を知覚していると結論付けられました。 たとえば、マッハの幻想：
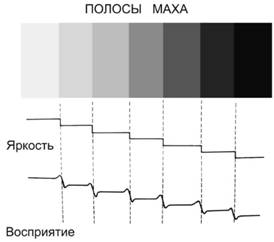
長方形の端には下線が引かれているようです。 それだけでなく、長方形の左の境界線は右よりも明るいように見えますが、実際には均一に色付けされています。 マッハのバンドは、網膜のレベルでさえ、対照的な境界が強調され、より強く知覚されることを示しています。 または、ここに光のコントラストの錯覚があります。
内側の正方形は明るさは同じですが、背景のために異なって知覚されます。 同じことが色知覚にも当てはまります。
色は補完的な背景でより明るく見えます。
したがって、 視覚情報の分析とパターン認識の前でさえ、目から脳への外界の印象は、異なる領域の異なる輪郭、色、明るさの情報のセットの形ですでに送信されています 。
ボーダーとその区別
網膜は、境界線を何らかのパラメーター（輝度、色調、長さ、方向）の変化として認識します。 網膜の境界を感知するには、強度の差がしきい値を超える必要があります。
実験の過程で、信号の知覚には、ウェーバーの法則と呼ばれる依存関係が有効であることがわかりました。「2つの信号を互いに区別できるように、それらの差は絶対値に比例する必要があります」
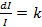ここで、私は知覚の強さです
同じ実験で、この式の係数kは約1/60であることがわかりました。 これはコンピューターの色にとって何を意味しますか？ RGBカラーモデルの明るさのグラデーションは、0〜255の256の値に対応します。したがって、黒い背景に明るい四角形（RGBモデルでは0の明るさ）を配置し、目が自信を持ってこの四角形の境界を固定できる場合、四角形の明るさは少なくとも5にする必要があります。
グラデーションはどうですか？ 明るさの増加の滑らかさはどのように知覚されますか？ Fechnerの法則と呼ばれる別の認識は、 流動性の認識にとって重要です。
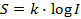ここで、Sは感覚の変化の差であり、Iは信号の実際の変化（たとえば、照明）です。
したがって、信号の立ち上がりを滑らかに感じるためには、指数関数的に変化させる必要があります。 この方程式の係数kは、ウェーバーの法則と同じ係数です。
スティーブンスのべき法則と呼ばれる次の関係は、信号の変化がどの程度強く知覚されるかを示しています。 たとえば、線の明るさまたは「長さ」の違いはどれほど強く認識されますか：
この方程式では、係数kはもはやウェーバー定数に関係せず、メトリックスケールの選択に依存し、係数bは影響の種類に応じて計算される定数です。
暗闇での明るさの場合、bは長さの知覚1.0に対して0.33と実験的に計算されます。 したがって、長さの知覚の場合、依存関係は次の形式を取ります。
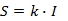
つまり 長さの知覚力は長さに正比例し、2センチの線は1センチの線の2倍の大きさのようです。
1アイツアー -2知覚 -3視界のジオメトリ -4アイトラッキング -5視線の捉え方 -6アイトラッキングのモデリング