1から1までの数字のランダムな順列を構築する必要があります $インライン$ n $インライン$ すべての順列が等しくなる可能性があります。 これは多くの方法で実行できます。たとえば、最初に最初の要素をランダムに選択し、次に残りの2番目の要素から選択するなどです。 または、別の方法で行うことができます：ポイントをランダムに選択 $インライン$ t_1、t_2、\ ldots、t_n $インライン$ セグメント内 $インライン$ [0,1] $インライン$ 、およびそれらの順序を確認します。 最小の数値を1に、2番目の数値を2に、というように置き換えると、ランダムな順列が得られます。 すべてが見やすい $インライン$ n！$インライン$ 順列も同様に考えられます。 それは可能であり、セグメントではありません $インライン$ 0.1 $インライン$ ポイントを選択し、たとえば、1〜 $インライン$ n $インライン$ 。 一致はここで可能です（セグメントについては可能ですが、確率はゼロであるため、気にすることはありません）-一致する数を追加で並べ替えるなど、さまざまな方法で対処できます。 または、偶然の確率が小さくなるようにNを大きくします（ $インライン$ N = 365 $インライン$ 、そして $インライン$ n $インライン$ クラスには生徒数があり、2人の誕生日の偶然について話している。）この方法のバリエーション：ランダムなメモ $インライン$ n $インライン$ 単位正方形内のポイントとそれらの縦座標が横座標に対してどのように順序付けられているかを確認します。 別のバリエーション：セグメント内のマーク $インライン$ n-1 $インライン$ ポイントし、分割されたセグメントの長さがどのように順序付けられているかを確認します。 これらのアプローチの重要な点は、テストの独立性であり、その結果によると、ランダムな順列が構築されます。 アンドレイ・ニコラエヴィッチ・コルモゴロフは、確率論は測定理論に独立性を加えたものであり、これは確率を扱った人なら誰でも確認できると述べた。
ツリーのフックの式の例を使用して、これがどのように役立つかを示します。
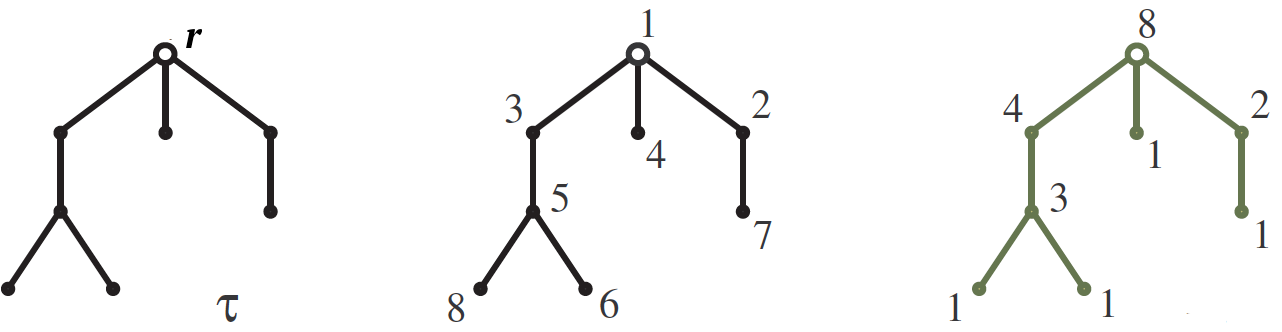
させる $インライン$ \ tau $インライン$ -ルートによって中断 $インライン$ r $インライン$ と木 $インライン$ n $インライン$ 写真のようにピークが下がっています。 私たちの目標は、数を計算することです $インライン$ S（\ tau）$インライン$ ナンバリングツリートップ $インライン$ \ tau $インライン$ 1から $インライン$ n $インライン$ そのため、各エッジの上部の数は下部の数よりも大きくなります。 これらの数字の1つが中央の図に示されています。 答えは、 フックサイズを使用して定式化されます。 フック $インライン$ H（v）$インライン$ ピーク $インライン$ v $インライン$ この頂点から成長するサブツリーを呼び出しましょう。そのサイズは、単にその中の頂点の数です。 フックの長さは、対応する頂点の隣の右側の図に記載されています。 だから、数字の数は等しい $インライン$ n！$インライン$ フックのサイズの製品で割ったので、この例では
$$表示$$ S（\ tau）= \、\ frac {8！} {8 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ cdot 1 \ cdot 1 \ cdot 1} = 210. $$ display $ $
たとえば、頂点の数の帰納法など、さまざまな方法でその式を証明できますが、ランダムな順列の私たちの見解により、計算なしで証明を実行することができます。 それは優雅さだけでなく、規定された不等式での番号付けに関するより微妙な質問によく一般化されているため、今ではそうではないためです。 したがって、 n個の異なる実数を取得し、それらをツリーの最上部にランダムに配置します。 $インライン$ n！$インライン$ 順列も同様に考えられます。 各エッジについて、エッジの上部頂点の数が下部頂点の数より大きい可能性はどのくらいですか？ 答えは： $インライン$ S（\ tau）/ n！$インライン$ 、そしてそれは数字のセットに依存しません。 そして、それが依存しない場合は、ランダムに選択された数字を考慮しましょう-明確にするために、間隔で $インライン$ [0,1] $インライン$ 。 最初に数字をランダムに選択してから、ツリーの最上部にランダムに配置する代わりに、各頂点で数字をランダムに独立して選択することができます。それらの再配置は自動的にランダムになります。 このように $インライン$ S（\ tau）/ n！$インライン$ これは、ランダムな独立した数値の確率です $インライン$ \ xi（v）$インライン$ 各頂点に選択されたもの $インライン$ v $インライン$ 木 $インライン$ \ tau $インライン$ 、形式のすべての不等式 $インライン$ \ xi（v）> \ xi（u）$インライン$ すべてのエッジに対して $ inline $ v \ to u $ inline $ 、 $インライン$ v $インライン$ rib骨の頂点です。 $インライン$ u $インライン$ -下。 これらの条件は同等の形式で定式化されますが、わずかに異なる方法で：各頂点に対して $インライン$ v $インライン$ そのようなイベントが発生するはずです-私はそれを指定します
$インライン$ Q（v）$インライン$ ：番号 $インライン$ \ xi（v）$インライン$ -フックサブツリーの頂点にあるすべての数値の最大値 $インライン$ H（v）$インライン$ 。
に注意してください $ inline $ \ frac {1} {| H（v）|} $ inline $ これはイベントの確率です $インライン$ Q（v）$インライン$ 。 実際には、フックで $インライン$ H（v）$インライン$ 利用可能です $インライン$ | H（v）| $インライン$ 頂点と最大フック番号が等しい確率でそれぞれにマッピングされます $ inline $ \ frac {1} {| H（v）|} $ inline $ 。 フック式 $ inline $ S（\ tau）/ n！= \ prod_v \ frac {1} {| H（v）|} $ inline $ 次のように定式化できます：すべてのイベントが一度に発生する確率 $インライン$ Q（v）$インライン$ これらのイベントの確率の積に等しい。 これにはさまざまな理由がありますが、最初に思い浮かぶのはここで動作します。これらのイベントは独立しています。 これを理解するために、例えばイベントを見てみましょう $インライン$ Q（r）$インライン$ （ルートに対応）。 これは、ルート内の数が頂点内の他のすべての数よりも大きいという事実から成り、他のイベントは、ルート内にない数で書かれた数同士の比較に関連しています。 それは $インライン$ Q（r）$インライン$ 数に関して $インライン$ \ xi（r）$インライン$ 他の頂点の数字のセット 、および他のすべてのイベントは、ルート以外の頂点の数字の順序です 。 すでに説明したように、「順序」と「多重度」は独立しているため、イベント $インライン$ Q（r）$インライン$ 他から独立しています。 ツリーを下って行くと、これらのイベントはすべて、独立したものであり、必要なものは後に続きます。
通常、フックの式は、ツリー内の頂点ではなく、若いダイアグラムのセルに番号を付ける式です
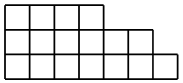座標軸の方向に増加し、そこにあるフックは木よりもフックのように見えます。 しかし、この式はより複雑であることが証明されており、別の投稿に値します。
ちなみに私は持っていたので、私はランダムなヤング図のモデルについて話さずにはいられません。 若い図は $インライン$ n $インライン$ 単位の正方形、行の長さは下から上へ、列の長さは左から右へ増加します。 ヤングのエリアチャートの数 $インライン$ n $インライン$ 示されている $インライン$ p（n）$インライン$ 、この重要な関数は興味深い異常な方法で動作します。たとえば、多項式よりも速く成長しますが、指数よりも遅くなります。 したがって、特に、ランダムなヤングダイアグラムを生成します（すべてのエリアダイアグラムが必要な場合 $インライン$ n $インライン$ 同様にそうだった $インライン$ 1 / p（n）$インライン$ ）些細な問題ではありません。 たとえば、セルを一度に1つずつ追加し、ランダムに追加する場所を選択すると、チャートごとに確率が異なります（したがって、単一線チャートの確率は等しくなります $インライン$ 1/2 ^ {n-1} $インライン$ 。）それは、図では面白い尺度であることがわかりますが、均一ではありません。 ユニフォームは次のようにして取得できます。 番号を取る $インライン$ t \ in（0,1）$インライン$ 、私たちの目的のために、エリア内の数字が最適です $インライン$ 1- \ mathrm {const} / \ sqrt {n} $ inline $ 。 それぞれについて $インライン$ k = 1,2、\ ldots $インライン$
平均を持つ非負整数の幾何分布を考える $インライン$ t ^ k $インライン$ （つまり、数の確率 $インライン$ m = 0,1、\ ldots $インライン$ 等しい $インライン$ t ^ {km}（1-t ^ k）$インライン$ ） それに応じてランダム変数を選択します $インライン$ m_k $インライン$ （これを整理する方法はたくさんあります）。 概して $インライン$ k $インライン$ 最も可能性の高い0。Young図を見てみましょう。 $インライン$ m_k $インライン$ 行は長さです $インライン$ k $インライン$ 毎回 $インライン$ k = 1,2、\ ldots $インライン$ 。 総面積が時々等しいので、私はそれをshipメソッドと呼びます $インライン$ n $インライン$ 。 等しくない場合は、実験を繰り返します。 実際に等しい $インライン$ n $インライン$ 賢く選択すれば彼女はしばしば十分です $インライン$ t \ in（0,1）$インライン$ 。 読者に、与えられた領域のすべての図が等しくなる可能性があることを独立して証明し、ステップ数を推定するように勧めます。