特にエンジニアが最も耐摩耗性が高く耐久性のあるベアリングを作成する場合、エンジニアは正確なコンピューターと物理モデリングを必要とします。その周囲とパラメーターは、ほぼ原子レベルで知られている必要があります。
想像してみてください。ベアリングの接触の正確な割合とモデルを見つけるためにプログラマにタスクを与えると、正確な円をシミュレートすることは不可能なので、これは不可能であることがわかります。 正確な接触面積をシミュレートすることは不可能なので。
円の概念は、文字通り任意の距離空間の場合に一般化できる普遍的な数学的概念の1つです。 しかし、コンピューターサイエンスのセクションでは、このトピックを取り上げることはほとんど不可能です。
それでは、円とは何ですか? そして、その正確な数学的モデルが不可能な理由。

科学的理解では、円は通常の65537多角形(65 5万5千および50 30の対角)-65 537の角と65 537の辺を持つ正多角形です。
プログラマーにとって、円は65 537角の多角形であり、これらの角度は平面または同じ円と接触し、65 537角の数学的円全体のバランスを変更します。 モデルがすでに古くなっていることに同意しますか?
1796年のガウスは、nの奇数の素因数が異なるフェルマー数であれば、コンパスと定規で通常のnゴンを構成できることを証明しました。 1836年、P。ワンゼルは、コンパスと定規のペアで構築できる他の正多角形がないことを証明しました。 今日、この声明はガウス-ワンゼルの定理として知られています。
科学は主に数値ではなく「範囲」で動作するため、品質の問題や周囲の状況を確認できない場合があるため、ベアリングの業界ではほとんどの自動車、鉄道、航空災害が正確に低品質のベアリングのために発生するほど狭い秘密を発見することさえできます。完全に滑らかなベアリングを作成する問題に起因するベアリング業界は最高です。
ゲームでこのような問題が発生します。
精度 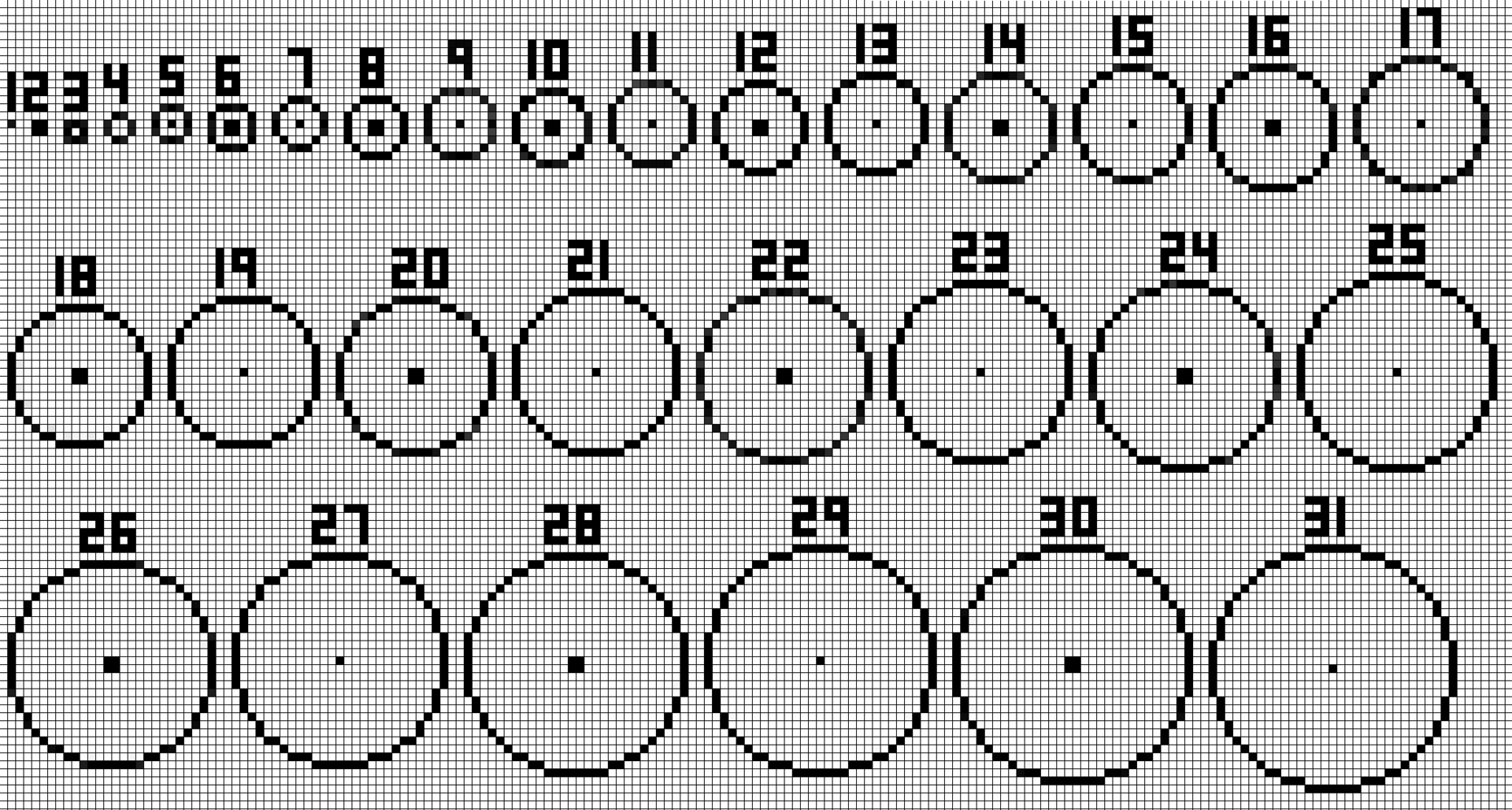

そして、この精度は非常に低いです。
また、円内の65,000の角度は100万未満です。

しかし、これでも制限ではありません。 理想的な円は一般に無限です(無限の数の角度を持っています)。 その数が不正確なモデルである場合、プログラミングでそれをどのように表現しますか? それとも、そのような高い精度は不要ですか? 実際、最小の詳細のマスモデリングでは、さまざまな結果をもたらすカスケードなだれのような効果が形成されます。
ご清聴ありがとうございました。