技術の潜在的な能力のリストには、観測にアクセスできない外乱のあるシステムの分析、そのようなシステムの共鳴特性の決定、外部励起のスペクトルとプロセス、それらの短い実現によるプロセスのスペクトル推定、低サンプリング周波数でのシステムの挙動のモデリングなどが含まれます。

エコノミスト(より正確には「計量経済学者」)によく知られているARMAプロセスは、自動調整の専門家にはあまり知られておらず、私の意見では、機械エンジニアや無線電子エンジニア、特に「古い学校」のものにはほとんど使用されていません。 この記事は、エンジニアリングの実践におけるARMA理論の適用のいくつかの可能な領域を示すことを試みています。
簡単に言えば、主題に不慣れな人のために、実際にはそれについてです。 明白な「デジタル」の理由による確率的連続時間プロセスx(t)は、実際には、通常、離散時間シーケンスx [i]とサンプリング間隔Δtに一致します。
原則として、任意のプロセスx [i]に対して、フォームの表現が可能です
x [i]-a 1・x [i-1]-a 2・x [i-2]-...-a p・x [ip] = b 0・f [i] + b 1・f [i- 1] + ... + b q・f [iq] (1)、
ここで、a kおよびb kは定数(このモデルの場合)係数であり、自己回帰pおよび移動平均qの次数を持つ自己回帰移動平均モデルと呼ばれます。 またはARMA(p、q)-model、f [i]は一種の「着信」プロセスであり、これについては少し低くなります。 多くの場合、(1)はわずかに異なる形式(6)で記述されます。
基本的には、再帰的なAR部分と非再帰的なMA部分の両方を備えた単なるデジタルフィルターです。
ARMA(p、q)モデルと線形システム(たとえば、機械的)には対応があります。たとえば、次の形式のよく知られた線形微分方程式で記述されます。
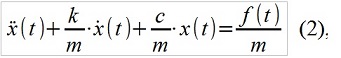
ここで、m、c、kは機械システムの質量、剛性、減衰、f(t)は外力です。 ARMAのカウンターパートは次のようになります。
x [i]-a 1・x [i-1]-a 2・x [i-2] = b 1・f [i-1] (3)、
モデルの係数は、線形システムとΔtの固有値λ1およびλ1 *(簡潔にするために、「振動する」ケースが考慮されます)を通じて非常に簡単に見つけることができます。
a 1 = z + z *、a 2 =-z z *、b 1 = j(z * -z)Δt/(2mω1)、
ここで、z = exp(λ1・Δt)、λ1 =-ε1 +jω1、jは虚数単位、*は複素共役
参照用:

テストシステムの場合、m = 1 kg、c = 100 N / m、k = 0.75 kg / s、Δt= 0.12 s、
ARMA(2,1)モデルを取得
x [i]-0.69433x [i-1] +0.91393 x [i-2] = 0.010696f [i-1]
(一般に(3)が(2)からどのように得られるかについての非常に簡単な説明。線形システムのパルス遷移関数、つまり単一パルスに対するシステムの応答:
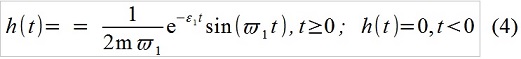
「積分」形式のレコード(2)は、「畳み込み」f(t)およびh(t)と呼ばれます。これは、外部アクションを一連の基本インパルスと見なすことを意味します。 離散時間では、たとえば次のように記述します。
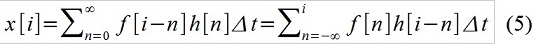
x [i]、x [i-1]、x [i-2]を選択した係数1、a 1 、a 2を使用して追加することにより、無限の「尾」の相互消滅を実現しますh [i]-f [i]は右側に残ります・H [0] = f [i]・0およびf [i-1]・h [1] = f [i-1]・b 1 ARMA理論の観点から、移動平均MA(∞)の無限次元モデルはARMA(2,1)に変換されます(純粋な自己回帰モデルAR(2)= ARMA(2,0)が偶然得られたと言う人もいます)。
備考1.プロセスのデジタル処理に精通している読者は、h(t)を離散化するだけではあまり正しくないことを言うでしょう。周波数の関数h(t)を1 /(2Δt)(フィルター処理)に制限する必要があります。 それ以外の場合、周波数マスキングエラーが存在します。 私たちのシステムの周波数応答と位相応答のグラフ、「分析」モデルとARMAモデルは、ほとんどのエンジニアリングケースでこのエラーを無視できる理由を示しています(図1)(ここで、周波数応答は対数スケールです)。
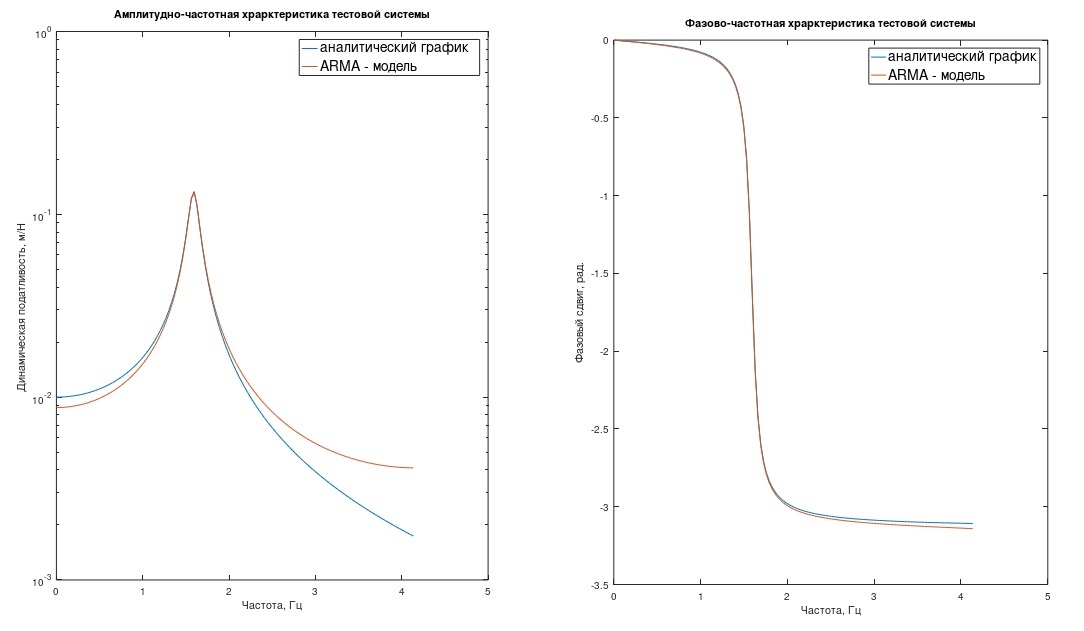
図1テストシステムの周波数応答と位相応答
備考2.実際には、ARMAモデルの次数は、機械システムのいくつかの自由度または実際の外部影響の複雑なスペクトルのために、上記で検討した例よりも大幅に大きくなる可能性があります。
備考3.非常に重要です。 結果のプロセスx [i]のみによってARMAモデルのパラメーター(つまり、pおよびqモデルの順序と係数a kおよびb k )を推定できるメソッド(ここでは考慮しません-それらについてさらに多くの記事を書くことができます)がありますf [i]は、分散も推定できる仮想のホワイトノイズである。 一般に、このような評価はARMA理論全体の主要部分です。 これらの方法は特定の完全性において違いはありませんが、かなり興味深いものです。
さて、実際に、これらすべてを実際に適用できる(または適用できる)理由について説明します。 非常に明白なことに加えて、最初の2点と2つの係数a 1およびa 2からの「手動」減衰(および減衰なし)正弦波の迅速な構築に加えて、工学的実践におけるこれらのモデルのより深刻な応用があります。
1.実際、システムのシミュレーションモデリングでは、入力に実際の外部信号f [i]を与え、出力でx [i]を取得します。
x [i] = a 1・x [i-1] + a 2・x [i-2] + ... + a p・x [ip] + b 0・f [i] + b 1・f [i- 1] + ... + b q・f [iq] (6)
ARMAモデルは、有限差分モデルよりもタスクをうまく処理しますが、これは大きなサンプリング間隔Δtでのみ顕著です。 (図2では、Δt= 0.12秒(左)および0.03秒)。 その場合、ARMAを台無しにするのは理にかなっています-あなたが決める
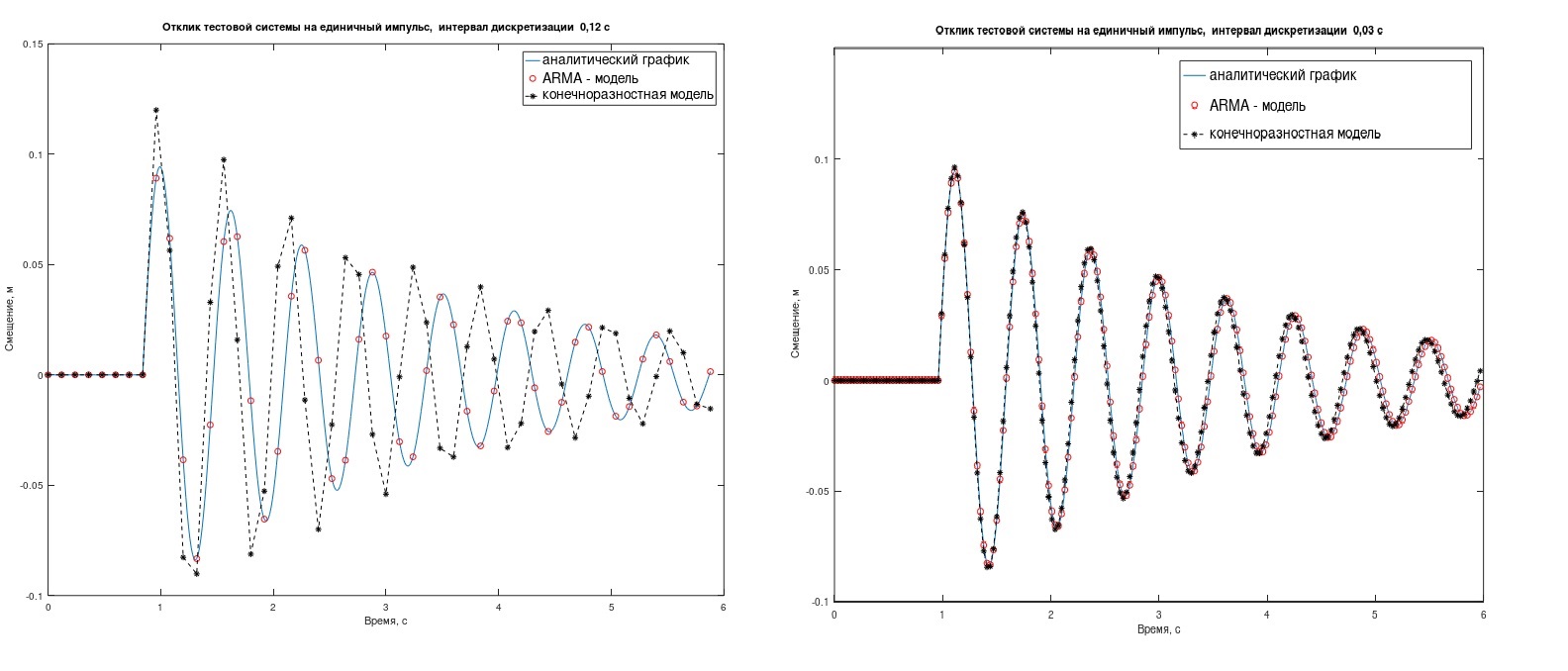
図 2.単一のインパルスに対するテストシステムの応答。
2.スペクトル推定、特に定常プロセスの実装長が観測に不十分な場合。 おそらく、これはARMAモデルの最も有名なエンジニアリングアプリケーションです。 調査中のプロセスでは、特定のデジタルフィルターとそれに入力されるホワイトノイズの分散が取得されるため、PSDの推定値を構築するタスクは明らかな方法で解決されます。 実際、外部から非常に「滑らかな」SPMグラフを取得し、同時に高解像度の印象を作り出すことができます。 アセスメントの予想される改善は、研究者がプロセスの性質に関する外部情報をアセスメントの構築にもたらすという事実に関連しています-通常、既知のモデル次数を設定することによって。
要するに、このPSDの概算を知る必要があります。 古典的な方法を使用したこの実装の「探索的」研究では、ほとんど同じことができませんが、主に類似した性質の古典的な(FFTに基づく)研究を参照しますが、かなり長い実現です。 重大なエラーが発生する可能性があります。
3.真の外部効果が観測に利用できない場合の、システムの共振特性と外部作用のスペクトルの分析。 既に述べたように、プロセスx [i]を知っていれば、モデルa kおよびb kのすべての係数(および着信ホワイトノイズの分散)を決定できます。 それらを使用して、対応する係数で2つの多項式の根を決定すると、モデルのp「極」とq「零点」(λkとμk)を見つけて伝達関数を構築するのは簡単です。おそらくARMA形式さえ使用できません(ここではそして、通常の「分析」形式で-上記で確認したように(図1)、違いはわずかです。 たとえば、p = 5の場合、q = 3(既存の、明らかに、pとqの比率に関する制限からこれまで注意をそらす)、オプションとして、次のものがあります。
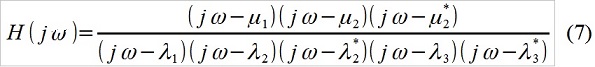
もちろん、すべてが非常に単純化されています。 調査中のオブジェクトの既知の性質(たとえば、車の乗り心地のポリゴンテスト)と外部衝撃(道路のミクロプロファイル)に基づいて、研究者は伝達関数を次のように書き換えることに決めました。
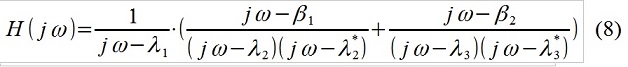
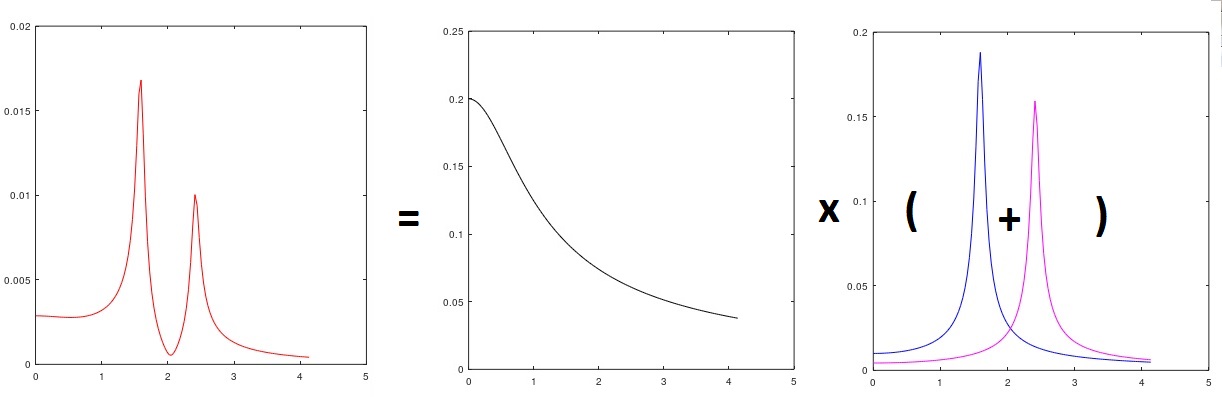
図3入ってくる外乱を強調した信号スペクトルの分析
そしてコメント-λ1に関連するモデルの部分は明らかに(入力された仮想ホワイトノイズの分散を2乗して乗算するまで)道路の「ピンク」のマイクロプロファイルです(図3)(つまり、実際の未知のスペクトルを識別しました着信信号(手動で選択)-「類似」のように見えます)、λ2およびλ3はサスペンション上の車体の共振特性です(縦振動モードと縦振動モードの可能性があります)。 もちろん、主な問題は、ARMAモデルのパラメーターを決定することです。 説明したばかりの場合、ARMAなしで、スペクトル密度グラフに従って旧式の方法(「電子形式」ではあるが)で「クロール」し、-3 dBなどのレベルでピーク幅を測定したり、曲線を適用したりすることができます。 。
3.線形予測x [i]の場合。 どうやら、ARMAの主な用途は計量経済学者向けです。 (6)からわかるように、モデルの係数が上記の方法を使用して推定された場合、次の値x [i]は観測できないホワイトノイズb 0・f [i]に対して正確に推定でき、このホワイトノイズの分散が推定されます。モデルの係数とともに。 通常、この場合、モデルパラメーターの動的な(リアルタイムの)調整が暗示されます。 どうやら、それはアクティブな振動と騒音低減のシステムで役立つことがあります。 TAPの専門家はよく知っています。
4.監視できないアクセスできないプロセスを復元する。 モデルをパーツに分割する場合、上記のセクション3に示すように、調査中のプロセスの性質に関する知識に基づいて、入ってくる摂動のスペクトルを個別に評価し、物理システムの振動特性を個別に評価することができます(モデルをパーツに分割します)。 さらに進むことができます-システムの出力を入力に接続するフィルター(元のモデルの逆モデル、ARMAモデル)を作成し、結果のプロセスx [i]の助けを借りて、入ってくる外乱の一時的な実装を取得します。 たとえば、正確に未知の線形歪みで記録された歪みのない信号を、別の研究にアクセスできない機器(たとえば、テレメトリで取得)で復元しようとします。
私の謙虚な知識に基づいて、結果としてそのような主観的な判断を表明します。 ARMAテクノロジーのエンジニアリング問題への適用可能性は、結果の信号からこれらのモデルのパラメーターを推定する方法の完成度に大きく依存します。むしろ、私の意見では、これらの方法の不完全性によって強く抑制されます。 エンジニアリングにおけるARMAの適用における経験の蓄積は、主に、この分野で非常にありそうな「ブレークスルー」を予想して、理にかなっているようです。