🏴󠁧󠁢󠁷󠁬󠁳󠁿 👃🏼 👩🏼‍💼 神経量子状態-ニューラルネットワークによる波動関数の表現 ☝🏿 😑 🏇🏽

この記事では、一般的なニューラルネットワークと限られたボルツマンマシンの異常な応用について、特に量子力学の2つの複雑な問題を解決するために検討します-基底状態エネルギーを見つけ、多体系の波動関数を近似します。

これは、2017年にScienceで発表された記事[2]の無料の簡略化されたリテールであると言えます。私は非常に興味深いように見えたが、この作品の人気のある科学的博覧会をロシア語（そしてこの英語版の1つだけ）で見つけることはできなかった。

量子力学と深層学習からの最小限の必須概念

これらの定義が非常に簡素化されていることにすぐに注意したいです。記述された問題が暗い森である人々のためにそれらを与えます。

状態は、システムを説明する物理量のセットです。たとえば、宇宙を飛行する電子の場合は座標と運動量になり、結晶格子の場合はノードにある原子のスピンのセットになります。

システムの波動関数は、システムの状態の複雑な関数です。スピンのセットなどの入力を受け取り、複素数を返すブラックボックス。私たちにとって重要な波動関数の主な特性は、その平方がこの状態の確率に等しいことです：

P s i （ s ） P s i （ s ）^{*} = P （ s ）

$\ Psi（s）\ Psi（s）^ * = P（s）$

波動関数の2乗を1に正規化することは論理的です（これも重要な問題の1つです）。

ヒルベルト空間 —この場合、そのような定義で十分です—システムのすべての可能な状態の空間。たとえば、値+1または-1を取ることができる40スピンのシステムの場合、ヒルベルト空間はすべて

2^{40}

$2 ^ {40}$ 可能な条件。値を取ることができる座標の場合

[- i n f t y 、 + i n f t y]

$[-\ infty、+ \ infty]$ 、ヒルベルト空間の次元は無限です。方程式を分析的に解くことのできない主な問題は、実システムのヒルベルト空間の巨大な次元です。プロセスでは、「正面」で計算できないヒルベルト空間全体の積分/合計があります。奇妙な事実：宇宙の生涯を通して、ヒルベルト空間の一部であるすべての可能な状態のほんの一部に会うことができます。これは、ヒルベルト空間全体と、空間の複雑さの特性（体、粒子、スピンなどの数）の多項式の後に満たされる可能性のある状態を概略的に示す、テンソルネットワークに関する記事の写真で非常によく示されています。

限定されたボルツマンマシン —説明が難しい場合、無向のグラフィカルな確率モデルであり、その制限は、同じ層のノードからの1つの層のノードの確率の条件付き独立性です。簡単な方法であれば、これは入力と1つの隠れ層を持つニューラルネットワークです。隠れ層のニューロンの出力の値は0または1です。通常のニューラルネットワークとの違いは、隠れ層のニューロンの出力は、活性化関数の値に等しい確率で選択されたランダム変数であるということです。

P_{i} （ 1 ） = s i g m a （ b_{i} + s u m_{j} W_{i j} s_{j} ）

$P_i（1）= \ sigma（b_i + \ sum_jW_ {ij} s_j）$

どこで

\シ グ マ

$\シグマ$ - シグモイド活性化機能、

b_{i}

$b_i$ -i番目のニューロンのオフセット、

W

$W$ -ニューラルネットワークの重み、

s_{j}

$s_j$ -可視レイヤー。限られたボルツマンマシンは、いわゆる「エネルギーモデル」に属します。これは、このマシンのエネルギーを使用してマシンの特定の状態の確率を表現できるためです。

E （ v 、 h ） = - a^{T} v - b^{T} h - v^{T} W h

$E（v、h）= -a ^ Tv-b ^ Th-v ^ TWh$

ここで、 vとhは可視層と非表示層、 aとbは可視層と非表示層の変位、 Wは重みです。状態の確率は次の形式で表現できます。

P （ v 、 h ） = f r a c 1 Z e^{- E （ v 、 h ）}

$P（v、h）= \ frac {1} {Z} e ^ {-E（v、h）}$

ここで、 Zは統計合計とも呼ばれる正規化項です（合計確率が1に等しくなるように必要です）。

はじめに

今日、限られた深層学習の専門家の間で意見があります

ボルツマンマシン（以下-OMB）は、実際のタスクには実質的に適用できない古い概念です。ただし、2017年にScienceで記事が公開され[2]、量子力学の問題に対するOMBの非常に効果的な使用が示されました。

著者は自明のように見えるかもしれない2つの重要な事実に気づいたが、それ以前には誰も考えもしていなかった。

OMBはニューラルネットワークであり、 Tsybenkoの普遍的な定理によれば、理論的には任意の高精度で任意の関数を近似できます（依然としてあらゆる種類の制限がありますが、それらをスキップできます）。
OMBは、各状態の確率が入力（可視レイヤー）、重み、ニューラルネットワークの変位の関数であるシステムです。

さらに著者は、システムをOMBエネルギーの根である波動関数で完全に記述し、OMB入力はシステムの状態の特性（座標、スピンなど）であると述べました。

P s i （ s ） = f r a c 1 Z s q r t e^{E （ s 、 h ）}

$\ Psi（s）= \ frac {1} {Z} \ sqrt {e ^ {E（s、h）}}$

ここで、sは状態の特性（スピンなど）、hはOMBの隠れ層の出力、EはOMBのエネルギー、Zは正規化定数（統計合計）です。

すべて、Scienceの記事の準備ができた後、ほんのわずかな詳細しか残っていません。たとえば、ヒルベルト空間のサイズが大きいため、計算不可能なパーティション関数の問題を解決する必要があります。そして、Tsybenkoの定理は、ニューラルネットワークが任意の関数を近似できることを教えてくれますが、これに適したネットワークの重みとオフセットのセットを見つける方法についてはまったく述べていません。さて、そしていつものように、楽しみはここから始まります。

モデルトレーニング

現在、元のアプローチにはかなりの変更がありますが、元の記事のアプローチのみを検討します[2]。

挑戦する

この場合、トレーニングタスクは次のようになります。最小エネルギーの状態を最も可能性の高い波動関数の近似値を見つけることです。これは直感的に明らかです：波動関数は状態の確率、ハミルトニアンの固有値（エネルギー演算子、またはより単純なエネルギー-この記事の枠組みではこの理解で十分です）が波動関数であるためです。すべてがシンプルです。

実際には、常に基底状態のエネルギー以上の別の量、いわゆるローカルエネルギーを最適化するように努力します。

E_{l o c} （ s i g m a ） = R e s u m_{s i g m a s i g m a^{'}} H_{s i g m a s i g m a^{'}} f r a c P s i （ s i g m a^{'} ） P s i （ s i g m a ）

$E_ {loc}（\ sigma）= Re \ sum _ {\ sigma \ sigma '} H _ {\ sigma \ sigma'} \ frac {\ Psi（\ sigma '）} {\ Psi（\ sigma）}$

こっち

\シ グ マ

$\シグマ$ 私たちの状態です

\シ グ マ^{'}

$\シグマ '$ -ヒルベルト空間のすべての可能な状態（実際には、より近似値を検討します）、

H_{s i g m a s i g m a^{'}}

$H _ {\ sigma \ sigma '}$ ハミルトニアンの行列要素です。特定のハミルトニアンに大きく依存しています。たとえば、イジングモデルの場合、これは単なる

f （ s i g m a ）

$f（\ sigma）$ もし

s i g m a = s i g m a^{'}

$\ sigma = \ sigma '$ 、そして

- c o n s t

$-const$ 他のすべての場合。ここで停止しないでください。これらの要素がさまざまな人気のあるハミルトニアンで見つかることが重要です。

最適化プロセス

サンプリング

元の記事のアプローチの重要な部分は、サンプリングプロセスです。 Metropolis-Hastingsアルゴリズムの修正版が使用されました。一番下の行は次のとおりです。

ランダムな状態から始めます。
ランダムに選択されたスピンの符号を反対に変更します（座標については他の修正がありますが、それらも存在します）。
確率が等しい $P（\ sigma '| \ sigma）= \ Big | {\ frac {\ Psi（\ sigma'）} {\ Psi（\ sigma）} \ Big | ^ 2$ 、新しい状態に移行します。
N回繰り返します。

その結果、波動関数が与える分布に従って選択されたランダムな状態のセットを取得します。各状態のエネルギー値とエネルギーの数学的期待値を計算できます

m a t h b b E （ E_{l o c} ）

$\ mathbb {E}（E_ {loc}）$ 。

エネルギー勾配の推定値（より正確には、ハミルトニアンの期待値）は次の値に等しいことが示されます。

G_{k} （ x ） = 2 * （ E_{l o c} （ x ） - m a t h b b E （ E_{l o c} ） ） * D_{k}^{*} （ x ）

$G_k（x）= 2 *（E_ {loc}（x）-\ mathbb {E}（E_ {loc}））* D ^ * _ k（x）$

おわりに

これは、2017年にG. Carleoが行った量子科学と量子テクノロジーの上級学校の講義からのものです。 Youtubeにエントリがあります。

注：

D_{k}^{*} （ x ） = f r a c p a r t i a l_{p_{k}} P s i （ x ） P s i （ x ）

$D ^ * _ k（x）= \ frac {\ partial_ {p_k} \ Psi（x）} {\ Psi（x）}$

次に：

p a r t i a l_{p_{k}} m a t h b b E （ H ） =

$\ partial_ {p_k} \ mathbb {E}（H）=$

p a r t i a l f r a c s u m_{x x^{'}} P s i^{*} （ x ） H_{x x^{'}} P s i （ x^{'} ） s u m_{x} | P s i （ x ） |^{2} =

$\ partial \ frac {\ sum_ {xx '} \ Psi ^ *（x）H_ {xx'} \ Psi（x '）} {\ sum_x | \ Psi（x）| ^ 2} =$

f r a c s u m_{x x^{'}} P s i^{*} （ x ） H_{x x^{'}} D_{k} （ x^{'} ） P s i （ x^{'} ） s u m_{x} | P s i （ x ） |^{2} + f r a c s u m_{x x^{'}} P s i^{*} （ x ） D_{k}^{*} （ x ） H_{x x^{'}} P s i （ x^{'} ） s u m_{x} | P s i （ x ） |^{2} -

$\ frac {\ sum_ {xx '} \ Psi ^ *（x）H_ {xx'} D_k（x '）\ Psi（x'）} {\ sum_x | \ Psi（x）| ^ 2} + \ frac {\ sum_ {xx '} \ Psi ^ *（x）D_k ^ *（x）H_ {xx'} \ Psi（x '）} {\ sum_x | \ Psi（x）| ^ 2}-$

f r a c s u m_{x x^{'}} P s i^{*} （ x ） H_{x x^{'}} P s i （ x^{'} ） s u m_{x} | P s i （ x ） |^{2} f r a c s u m_{x} | P s i （ x ） |^{2} （ D_{k} （ x ） - D_{k}^{*} （ x ） ） s u m_{x} | P s i （ x ） |^{2} =

$\ frac {\ sum_ {xx '} \ Psi ^ *（x）H_ {xx'} \ Psi（x '）} {\ sum_x | \ Psi（x）| ^ 2} \ frac {\ sum_x | \ Psi （x）| ^ 2（D_k（x）-D ^ * _ k（x））} {\ sum_x | \ Psi（x）| ^ 2} =$

f r a c s u m_{x x^{'}} f r a c P s i^{*} （ x ） P s i^{*} （ x^{'} ） H_{x x^{'}} D_{k} （ x^{'} ） | P s i （ x^{'} ） |^{2} + s u m_{x x^{'}} | P s i （ x ） |^{2} H_{x x^{'}} D_{k}^{*} （ x^{'} ） f r a c P s i （ x^{'} ） P s i （ x ） s u m_{x} | P s i （ x ） |^{2} -

$\ frac {\ sum_ {xx '} \ frac {\ Psi ^ *（x）} {\ Psi ^ *（x'）} H_ {xx '} D_k（x'）| \ Psi（x '）| ^ 2 + \ sum_ {xx '} | \ Psi（x）| ^ 2H_ {xx'} D ^ * _ k（x '）\ frac {\ Psi（x'）} {\ Psi（x）}} {\ sum_x | \ Psi（x）| ^ 2}-$

m a t h b b E （ H ） f r a c s u m_{x} | P s i （ x ） |^{2} （ D_{k} （ x ） + D_{k}^{*} （ x ） ） s u m_{x} | P s i （ x ） |^{2} \約

$\ mathbb {E}（H）\ frac {\ sum_x | \ Psi（x）| ^ 2（D_k（x）+ D ^ * _ k（x））} {\ sum_x | \ Psi（x）| ^ 2 } \約$

m a t h b b E （ E_{l o c} D_{k}^{*} ） - m a t h b b E （ E_{l o c} ） m a t h b b E （ D_{k}^{*} ） + C

$\ mathbb {E}（E_ {loc} D ^ * _ k）-\ mathbb {E}（E_ {loc}）\ mathbb {E}（D ^ * _ k）+ C$

次に、最適化の問題を解決します。

OMBから状態をサンプリングします。
各状態のエネルギーを計算します。
勾配を推定します。
OMBの重みを更新します。

結果として、エネルギー勾配はゼロになる傾向があり、メトロポリス・ヘイスティングスプロセスの一意の新しい状態の数と同様に、エネルギー値は減少します。これは、真の波動関数からサンプリングすることにより、ほぼ常に基底状態になるためです。直感的には、これは論理的に思えます。

元の研究では、小規模なシステムの場合、基底状態エネルギーの値が取得されましたが、これは分析的に得られた正確な値に非常に近いものでした。基底状態のエネルギーを見つけるためのよく知られているアプローチと比較が行われ、特に既知の方法と比較してNQSの計算の複雑さが比較的低いことを考慮して、NQSが勝ちました。

NetKet-「発明者」アプローチのライブラリ

元の記事[2]の著者の1人は、彼のチームと共に、非常に最適化された（私の意見では）Cカーネルと高レベルの抽象化で動作するPython APIを含む優れたNetKetライブラリ[3]を開発しました。

ライブラリはpipを介してインストールできます。 Windows 10ユーザーは、Windows用のLinuxサブシステムを使用する必要があります。

+ -1 / 2の値をとる40スピンのチェーンの例として、ライブラリの操作を検討してください。隣接相互作用を考慮に入れたハイゼンベルグモデルを検討します。

NetKetには、何をどのようにすればよいかをすばやく把握できる優れたドキュメントがあります。多くの組み込みモデル（背中、ボソン、イジング、ハイゼンベルグモデルなど）と、モデルを完全に自分で記述する機能があります。

カウントの説明

すべてのモデルはグラフで表示されます。チェーンには、1次元で周期的な境界条件を備えた組み込みのHypercubeモデルが適しています。

import netket as nk graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

ヒルベルト空間の説明

ヒルベルト空間は非常に単純です-すべてのスピンは+1/2または-1/2の値を取ることができます。この場合、スピンの組み込みモデルが適しています。

 hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

ハミルトニアンの説明

すでに書いたように、この場合、ハミルトニアンは、組み込み演算子があるハイゼンベルグハミルトニアンです。

 hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

RBMの説明

NetKetでは、スピン用に既製のRBM実装を使用できます-これは私たちの場合です。しかし、一般的に多くの車があります、あなたは異なるものを試すことができます。

 nk.machine.RbmSpin(hilbert=hilbert, alpha=4) machine.init_random_parameters(seed=42, sigma=0.01)

ここで、alphaは、隠れ層のニューロンの密度です。可視およびアルファ4の40個のニューロンの場合、160個ありますが、番号で直接示す別の方法があります。 2番目のコマンドは、

N （ 0 、 s i g m a ）

$N（0、\ sigma）$ 。この場合、シグマは0.01です。

サムラー

サンプラーは、ヒルベルト空間上の波動関数によって与えられる分布からのサンプルによって返されるオブジェクトです。上記のMetropolis-Hastingsアルゴリズムを使用して、タスクに合わせて修正します。

 sampler = nk.sampler.MetropolisExchangePt( machine=machine, graph=graph, d_max=1, n_replicas=12 )

正確には、サンプラーは上記のアルゴリズムよりも複雑なアルゴリズムです。ここでは、同時に最大12個のオプションを同時にチェックして、次のポイントを選択します。しかし、原則は一般に同じです。

オプティマイザー

これは、モデルの重みを更新するために使用されるオプティマイザーについて説明しています。より「なじみのある」領域でニューラルネットワークを使用した個人的な経験に基づいて、最良かつ最も信頼性の高いオプションは、少し古くなった確率的勾配降下です（詳細はこちら）。

 opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

トレーニング

NetKetには、教師なし（私たちの場合）と教師ありの両方のトレーニングがあります（たとえば、いわゆる「量子トモグラフィー」ですが、これは別の記事のトピックです）。私たちは単に「教師」について説明するだけです。

 vc = nk.variational.Vmc( hamiltonian=hamiltonian, sampler=sampler, optimizer=opt, n_samples=1000, use_iterative=True )

変分モンテカルロは、最適化する関数の勾配をどのように評価するかを示します。 n_smaples

は、サンプラーが返す分布からのサンプルのサイズです。

結果

次のようにモデルを実行します。

 vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

ライブラリはOpenMPIを使用して構築され、スクリプトは次のように実行する必要がありますmpirun -n 12 python Main.py

（12はコアの数です）。

私が受け取った結果は次のとおりです。

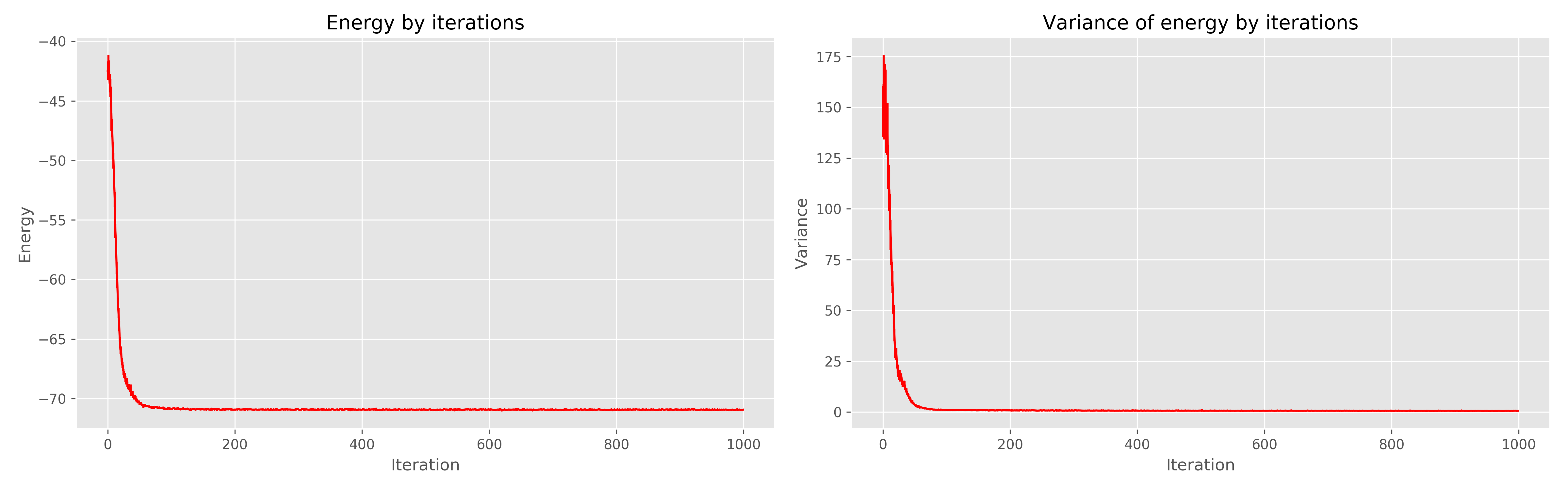
左側は学習の時代からのエネルギーグラフ、右側は学習の時代からのエネルギーの分散です。

1000の時代は明らかに冗長であり、300で十分であったことがわかります。

文学

OrúsR.テンソルネットワークの実用的な紹介：マトリックスの製品状態と予測されたエンタングルドペアの状態 -2014.-T.349。-S. 117-158。
Carleo G.、Troyer M.人工ニューラルネットワークによる量子多体問題の解決//科学。 -2017。-T.355。-いいえ。 6325。-S. 602-606。
www.netket.org

神経量子状態-ニューラルネットワークによる波動関数の表現