
実験データのヒストグラムの問題は何ですか
工業企業における製品品質管理の基礎は、実験データの収集とその後の処理です。
実験結果の初期処理には、データの分布の法則に関する仮説の比較が含まれます。これは、観測されたサンプルのランダム変数を最小の誤差で記述します。
このため、サンプルは、 長さの間隔で構築された列 。
また、測定結果の分布の形状を特定するには、さまざまな分布で解決効率が異なる(たとえば、最小二乗法を使用したり、エントロピー推定値を計算したりする)多くの問題が必要です。
さらに、すべての推定値の分散(標準偏差、過剰、過剰、反過剰など)も分布則の形式に依存するため、分布の識別も必要です。
実験データの分布形式を特定できるかどうかは、サンプルサイズに依存します。サンプルサイズが小さい場合、分布の特徴はサンプル自体のランダム性によってマスクされます。 実際には、さまざまな理由で、たとえば1000を超える大きなサンプルサイズを提供することはできません。
このような状況では、さらに一連の分析と計算に間隔シリーズが必要な場合に、間隔でサンプルデータを最適な方法で配布することが重要です。
したがって、識別を成功させるには、間隔の数kを割り当てる問題を解決する必要があります。
A. Haldは彼の本[1]で、これらの間隔で構築されたヒストグラムの段階的なエンベロープが一般母集団の滑らかな分布曲線に最も近い場合、最適な数のグループ化間隔があると広く確信しています。
最適値に近づく実用的な兆候の1つは、ヒストグラムのディップの消失であり、最大kは最適値に近いと見なされます。この場合、ヒストグラムは依然として滑らかな特性を保持します。
明らかに、ヒストグラムのタイプは、ランダム変数に属する区間の構成に依存しますが、均一なパーティションの場合でも、そのような構成の満足できる方法はまだ利用できません。
正しいと考えられるパーティションは、おそらく連続的な分布密度(ヒストグラム)の区分的定数関数による近似誤差が最小になるという事実につながります。
この問題は、推定密度が不明であるために発生します。したがって、間隔の数は最終サンプルの度数分布の形式に大きく影響します。
サンプル長が固定されている場合、パーティション間隔の拡大は、それらに到達する経験的確率の精密化だけでなく、情報の不可避的な損失(一般的な意味および確率密度分布曲線の意味の両方)にもつながります。したがって、さらに不当な拡大により、研究された分布はあまりにも滑らかになります。
一度発生すると、ヒストグラムの下の範囲を最適に分割するタスクは専門家の視野から消えることはなく、そのソリューションに関する唯一の確立された意見が現れるまで、タスクは関連したままになります。
実験データのヒストグラムの品質を評価するための基準の選択
ピアソンの基準では、既知のように、サンプルを区間に分割する必要があります。採用されたモデルと比較されたサンプルとの違いが評価されるのは区間です。
ここで: -実験周波数 ; -同じ列の頻度値、m列のヒストグラム列。
ただし、通常はヒストグラムの作成に使用される一定長の間隔の場合にこの基準を適用するのは非効率的です。 したがって、ピアソン基準の有効性に関する研究では、間隔は長さが等しいとは見なされませんが、受け入れられたモデルに従って確率が等しいと見なされます。
ただし、この場合、等しい長さの区間の数と等しい確率の区間の数は数倍異なります(等しく確率の高い分布を除く)。これにより、[2]で得られた結果の信頼性を疑うことができます。
近接性の基準として、エントロピー係数を使用することをお勧めします。エントロピー係数は次のように計算されます[3]。
ここで: -i番目の区間の観測数
エントロピー係数とnumpy.histogramモジュールを使用して実験データのヒストグラムの品質を評価するアルゴリズム
モジュールを使用するための構文は次のとおりです[4]。
numpy.histogram(a、bins = m、range = None、normed = None、weights = None、density = None)
numpy.histogramモジュールに実装されているヒストグラム分割間隔の最適な数mを見つける方法を検討します。
• 「auto」 - 「sturges」および「fd」の最大評価は、良好なパフォーマンスを提供します。
• 'fd'(Freedman Diaconis Estimator) -データのばらつきとサイズを考慮に入れた信頼性のある(放射耐性の)評価者。
• 'doane'-サージ推定の改良バージョン。非正規分布のデータセットでより正確に機能します。
• 「スコット」は、データのばらつきとサイズを考慮した信頼性の低い評価者です。
• 「ストーン」 -評価者は、誤差の二乗の推定値のクロスチェックに基づいており、スコットの規則の一般化と見なすことができます。
• 「米」 -評価者は変動性を考慮せず、データのサイズのみを考慮し、多くの場合、必要な間隔数を過大評価します。
• 「sturges」 -データのサイズのみを考慮した方法(デフォルト)は、ガウスデータに対してのみ最適であり、大きな非ガウスデータセットの区間数を過小評価します。
• 'sqrt'は、Excelおよび他のプログラムが間隔数をすばやく簡単に計算するために使用するデータサイズの平方根推定量です。
アルゴリズムの説明を開始するために、numpy.histogram()モジュールを適応させてエントロピー係数とエントロピー誤差を計算します:
from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:# m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]# h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)# ke=h/std (a)# (1). return ke,h
次に、アルゴリズムの主要な段階を検討します。
1) 実験データの処理におけるエラーの要件を満たす対照サンプル(以下「大サンプル」と呼びます )を作成します 。 大きなサンプルから、奇数のメンバーをすべて削除することにより、小さなサンプル(以下「小さなサンプル」と呼びます)を形成します。
2)すべての評価者「auto」、「fd」、「doane」、「scott」、「stone」、「rice」、「sturges」、「sqrt」について、大きなサンプルとエントロピー係数ke2のエントロピー係数ke1とエラーh1を計算します小さいサンプルの誤差h2と差の絶対値-abs(ke1-ke2);
3)少なくとも4つの間隔のレベルで評価者の数値を制御し、絶対差の最小値-abs(ke1-ke2)を提供する評価者を選択します。
4)評価者の選択に関する最終決定では、1つのヒストグラムに大小のサンプルの分布を構築し、評価者がabsの最小値(ke1-ke2)を提供し、評価者がabsの最大値を提供します(ke1-ke2)。 2番目のヒストグラムの小さなサンプルに追加のジャンプが現れると、最初の評価者の正しい選択が確認されます。
出版物からのデータのサンプルに対する提案されたアルゴリズムの作業を検討してください[2]。 データは、500から80個のブランクをランダムに選択し、その後の質量を測定することで得られました。 ワークの質量は、次の制限内でなければなりません。 kg 次のリストを使用して、最適なヒストグラムパラメーターを決定します。
リスティング
import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:# m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]# h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)# ke=h/std (a)# return ke,h a =array([17.37, 17.06, 16.96, 16.83, 17.34, 17.45, 17.60, 17.30, 17.02, 16.73, 17.08, 17.28, 17.08, 17.21, 17.29,17.47, 16.84, 17.39, 16.95, 16.92, 17.59, 17.28, 17.31, 17.25, 17.43,17.30, 17.18, 17.26, 17.19, 17.09,16.61, 17.16, 17.17, 17.06, 17.09,16.83, 17.17, 17.06, 17.59, 17.37,17.09, 16.94, 16.76, 16.98, 16.70, 17.27, 17.48, 17.21, 16.74, 17.12,17.33, 17.15, 17.56, 17.45, 17.49,16.94, 17.28, 17.09, 17.39, 17.05, 16.97, 17.16, 17.38, 17.23, 16.87,16.84, 16.94, 16.90, 17.27, 16.93,17.25, 16.85, 17.41, 17.37, 17.50,17.13, 17.16, 17.05, 16.68, 17.56 ] ) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print(" (n=80) : %s"%round(std(a),3)) print(" (n=80):%s"%round(mean(a),3)) print(" (n=40): %s"%round(std(b),3)) print(" (n=40): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title(' : %s \n abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()
取得するもの:
サンプルの標準偏差(n = 80):0.24
サンプルの数学的期待値(n = 80):17.158
サンプルの平均二乗偏差(n = 40):0.202
サンプルの数学的期待値(n = 40):17.138
ke1 = 1.95、h1 = 0.467、ke2 = 1.917、h2 = 0.387、dke = 0.033、m =自動
ke1 = 1.918、h1 = 0.46、ke2 = 1.91、h2 = 0.386、dke = 0.008、m = fd
ke1 = 1.831、h1 = 0.439、ke2 = 1.917、h2 = 0.387、dke = 0.086、m = doane
ke1 = 1.918、h1 = 0.46、ke2 = 1.91、h2 = 0.386、dke = 0.008、m = scott
ke1 = 1.898、h1 = 0.455、ke2 = 1.934、h2 = 0.39、dke = 0.036、m =石
ke1 = 1.831、h1 = 0.439、ke2 = 1.917、h2 = 0.387、dke = 0.086、m =米
ke1 = 1.95、h1 = 0.467、ke2 = 1.917、h2 = 0.387、dke = 0.033、m =サージ
ke1 = 1.831、h1 = 0.439、ke2 = 1.917、h2 = 0.387、dke = 0.086、m = sqrt
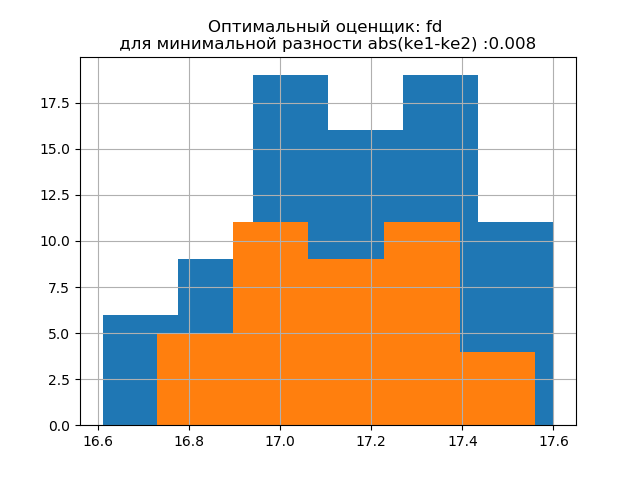
大きなサンプルの分布形式は、小さなサンプルの分布形式に似ています。 スクリプトから次のように、 「fd」は信頼性の高い(放射耐性の)評価者であり、データのばらつきとサイズを考慮します。 この場合、小さなサンプルのエントロピー誤差はわずかに減少します:h1 = 0.46、h2 = 0.386、エントロピー係数はk1 = 1.918からk2 = 1.91にわずかに減少します。

大小のサンプルの分布パターンは異なります。 説明が示すように、「doane」は「sturges」スコアの改良版であり、非正規分布のデータセットでより適切に機能します。 両方のサンプルで、エントロピー係数は2に近く、分布は通常に近いこのヒストグラム上の小さなサンプルでの追加のジャンプの出現は、前のものと比較して、評価者'fd'の正しい選択をさらに示します。
次の関係を使用して、パラメーターmu = 20、シグマ= 0.5、サイズ= 100の正規分布の2つの新しいサンプルを生成します。
a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)])
開発したメソッドは、次のプログラムを使用して取得したサンプルに適用できます。
リスティング
import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:# m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]# h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)# ke=h/std (a)# return ke,h #a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)]) a=array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945,20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print(" (n=100):%s"%round(std(a),3)) print(" (n=100):%s"%round(mean(a),3)) print(" (n=50):%s"%round(std(b),3)) print(" (n=50): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title(' : %s \n abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()
取得するもの:
サンプルの標準偏差(n = 100):0.524
サンプルの数学的期待値(n = 100):19.992
サンプルの平均二乗偏差(n = 50):0.462
サンプルの数学的期待値(n = 50):20.002
ke1 = 1.979、h1 = 1.037、ke2 = 2.004、h2 = 0.926、dke = 0.025、m =自動
ke1 = 1.979、h1 = 1.037、ke2 = 1.915、h2 = 0.885、dke = 0.064、m = fd
ke1 = 1.979、h1 = 1.037、ke2 = 1.804、h2 = 0.834、dke = 0.175、m = doane
ke1 = 1.943、h1 = 1.018、ke2 = 1.934、h2 = 0.894、dke = 0.009、m = scott
ke1 = 1.943、h1 = 1.018、ke2 = 1.804、h2 = 0.834、dke = 0.139、m =石
ke1 = 1.946、h1 = 1.02、ke2 = 1.804、h2 = 0.834、dke = 0.142、m =米
ke1 = 1.979、h1 = 1.037、ke2 = 2.004、h2 = 0.926、dke = 0.025、m =サージ
ke1 = 1.946、h1 = 1.02、ke2 = 1.804、h2 = 0.834、dke = 0.142、m = sqrt
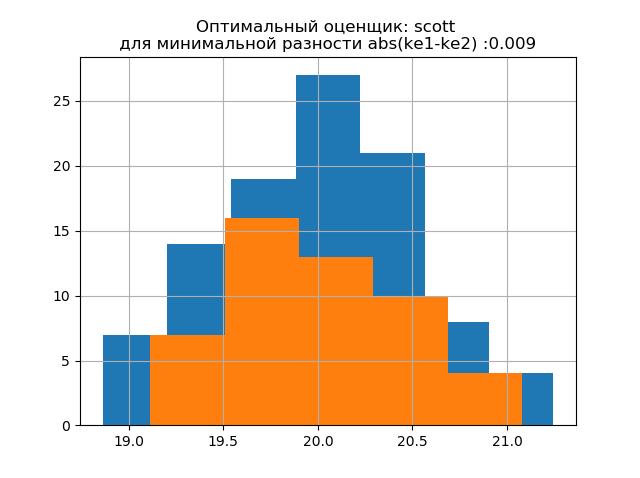
大きなサンプルの分布形式は、小さなサンプルの分布形式に似ています。 説明からわかるように、 「スコット」は、データのばらつきとサイズを考慮した信頼性の低い評価者です。 この場合、小さなサンプルのエントロピーエラーはわずかに減少します。h1= 1.018およびh2 = 0.894で、k1 = 1.943からk2 = 1.934にエントロピー係数がわずかに減少します。 。 新しいサンプルでは、前の例と同じようにパラメーターを変更する傾向があることに注意してください。

大小のサンプルの分布パターンは異なります。 説明からわかるように、 「doane」は「sturges」推定の改良版であり、非正規分布のデータセットでより正確に機能します。 両方のサンプルで、分布は正常です。 前のヒストグラムと比較して、このヒストグラムの小さなサンプルに追加のジャンプが出現することは、 スコット評価者の正しい選択をさらに示しています。
ヒストグラムの比較分析のためのアンチエイリアスの使用
大小のサンプルに基づいて作成されたヒストグラムを平滑化すると、より大きなサンプルに含まれる情報を保存するという観点から、より正確にそれらの同一性を判断できます。 最後の2つのヒストグラムを平滑化関数として想像してください。
リスティング
from numpy import* from scipy.interpolate import UnivariateSpline from matplotlib import pyplot as plt a =array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945, 20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] plt.title(' \n abs(ke1-ke2)' ,size=12) z=histogram(a, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label=' n=100') z=histogram(b, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label=' n=50') plt.legend(loc='best') plt.grid() plt.show() plt.title(' \n abs(ke1-ke2)' ,size=12) z=histogram(a, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label=' n=100') z=histogram(b, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label=' n=50') plt.legend(loc='best') plt.grid() plt.show()
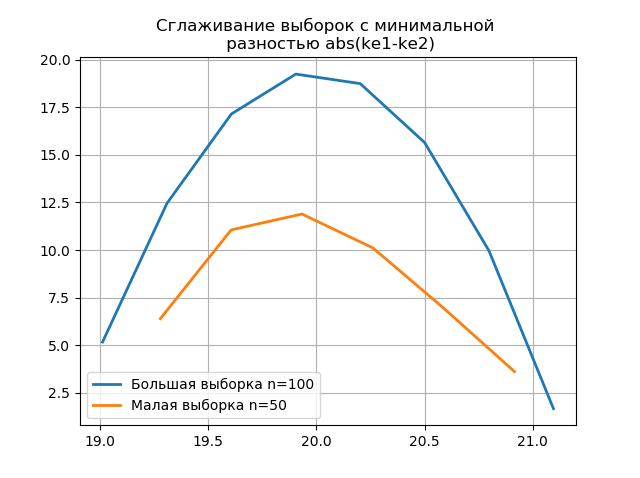
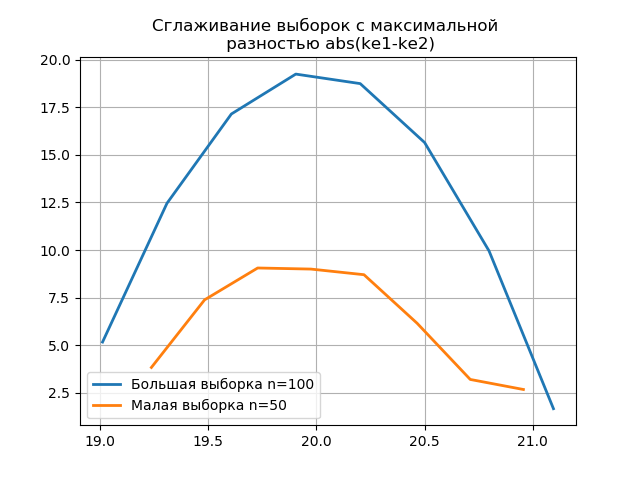
平滑化されたヒストグラムのグラフ上の小さなサンプルで、前のものと比較して追加のジャンプが出現することは、 スコットエバリュエーターの正しい選択をさらに示しています。
結論
生産で一般的な小さいサンプルの範囲で記事で提示された計算は、ボリュームの減少でサンプルの情報内容を維持する基準としてエントロピー係数を使用する効率を確認しました 。 組み込みのエバリュエーターでnumpy.histogramモジュールの最新バージョンを使用する手法が考慮されます-「auto」、「fd」、「doane」、「scott」、「stone」、「rice」、「sturges」、「sqrt」は最適化に十分です区間推定値に関する実験データの分析。
参照:
1. Hald A.技術的アプリケーションを使用した数学的統計。 -モスクワ:出版社。 lit.、1956
2. Kalmykov V.V.、Antonyuk F.I.、Zenkin N.V.
間隔推定のための実験データのグループ化クラスの最適数の決定//南シベリア科学会報— 2014. — No. 3. — P. 56-58。
3. Novitsky P. V.エラーのエントロピー値の概念//測定手法— 1966. — No. 7. —S。 11-14。
4. numpy.histogram-NumPy v1.16マニュアル