さらに異なるぼかしが必要

ガウスぼかしフィルターによる画像のぼかしは、さまざまなアプリケーションで広く使用されています。 しかし、場合によっては、調整に役立つパラメーターが1つだけであるサイズ（サイズ）だけでなく、すべての場合に1つのフィルターよりも少し多様性が必要な場合があります。 この記事では、他のぼかしの実装をいくつか見ていきます。

はじめに

ガウスぼかし効果は線形演算であり、フィルターマトリックスによる画像の畳み込みを数学的に表します。 さらに、画像内の各ピクセルは、特定の重み係数で取得された近くのピクセルの合計で置き換えられます。



フィルターは、ガウスと呼ばれる関数から構築されているため、ガウスと呼ばれます。 $$$e ^ {-x ^ 2}$ ：







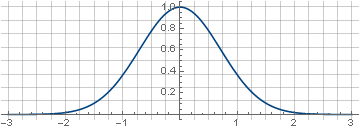
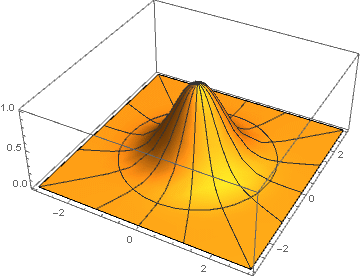
2次元バージョンは、縦座標軸を中心とした回転によって取得されます。 $$$e ^ {-（x ^ 2 + y ^ 2）}$ ：







座標の各ペアについて $$$（x、y）$ 中心までの距離は次の式で計算されます $$$\ sqrt {x ^ 2 + y ^ 2}$ 、ガウス関数への引数として渡されます-簡単にわかるように、 $$$e ^ {-\左（\ sqrt {x ^ 2 + y ^ 2} \右）^ 2}$ に減少 $$$e ^ {-（x ^ 2 + y ^ 2）}$ 。



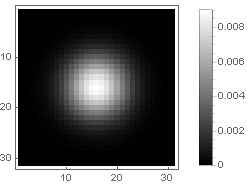
セグメント上に構築されたマトリックス $$$[-3.3]$ ある程度のサンプリングでは、次のようになります。

$$

$$\ left（\ begin {array} {ccccccc} 1.52 \ times 10 ^ {-8}＆2.26 \ times 10 ^ {-6}＆0.0000454＆0.000123＆0.0000454＆2.26 \ times 10 ^ {-6}＆1.52 \回10 ^ {-8} \\ 2.26 \回10 ^ {-6}＆0.000335＆0.00674＆0.0183＆0.00674＆0.000335＆2.26 \回10 ^ {-6} \\ 0.0000454＆0.00674＆0.135＆0.368＆0.135 ＆0.00674＆0.0000454 \\ 0.000123＆0.0183＆0.368＆1.00＆0.368＆0.0183＆0.000123 \\ 0.0000454＆0.00674＆0.135＆0.368＆0.135＆0.00674＆0.0000454 \\ 2.26 \ times 10 ^ {-6}＆0.000335＆0.00674＆ 0.0183＆0.00674＆0.000335＆2.26 \ times 10 ^ {-6} \\ 1.52 \ times 10 ^ {-8}＆2.26 \ times 10 ^ {-6}＆0.0000454＆0.000123＆0.0000454＆2.26 \ times 10 ^ { -6}＆1.52 \回10 ^ {-8} \\ \ end {array} \ right）$$

または、次のように、マトリックス要素の値を輝度レベルと見なす場合：







信号処理の観点では、これはインパルス応答と呼ばれます。これは、このフィルターと単一のインパルス（この場合はピクセル）の畳み込みの結果が正確に見えるためです。



最初に、ガウスは無限の間隔で定義されます。 しかし、かなり急速に減衰するため、ゼロに近い値は結果に影響しないため、計算から除外できます。 実際のアプリケーションでは、畳み込み後に画像の明るさが変わらないように、値の正規化も必要です。 また、各ピクセルが同じ色である画像をぼかす場合、画像自体は変更しないでください。



便宜上、座標に追加パラメーターを導入することにより、正規化もよく使用されます $$$\シグマ$ （「シグマ」と読む）-範囲内の引数を考慮する $$$[-1,1]$ 、そして $$$\シグマ$ ガウスの圧縮率を決定します。

$$

$$\ frac {e ^ {-\ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}}}} {2 \ pi \ sigma ^ 2}$$

正規化ディバイダー $$$2 \ pi \ sigma ^ 2$ ここで、無限大での定積分により分析的に得られます：

$$

$$\ int _ {-\ infty} ^ {\ infty} \ int _ {-\ infty} ^ {\ infty} e ^ {-\ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}} \、 dx dy = 2 \ pi \ sigma ^ 2$$

平等が成り立つという事実のために $$$e ^ {-\左（x ^ 2 + y ^ 2 \右）} = e ^ {-x ^ 2} e ^ {-y ^ 2}$ 、ガウスぼかしは、最初に行で、次に列で順番に実装できます。これにより、計算を大幅に節約できます。 この場合、1次元の場合の正規化式を使用する必要があります-

$$

$$\ frac {e ^ {-\ frac {x ^ 2} {2 \ sigma ^ 2}}}} {\ sqrt {2 \ pi \ sigma ^ 2}}$$

開始する

任意のフィルターの場合、最初に1つの変数から独自の減衰関数を定義する必要があります $$$f$ 、2つの変数の関数は、 $$$x$ に $$$\ sqrt {x ^ 2 + y ^ 2}$ どこで $$$x$ そして $$$y$ これらは、範囲内の行列要素の座標です $$$（-1,1）$ 、さらにマトリックスの要素を設定するために使用されます。 正規化は分析的には考慮されませんが、マトリックスのすべての要素の直接的な合計-これはより単純かつ正確です-離散化後、関数は「間引かれ」、正規化値は離散化のレベルに依存するためです。



行列の要素にゼロから番号が付けられている場合、座標 $$$x$ または $$$y$ 式によって計算されます

$$

$$\ frac {2インデックス} {サイズ-1} -1$$

どこで $$$インデックス$ -行または列の要素のシリアル番号、および $$$サイズ$ -要素の総数。



たとえば、5 x 5マトリックスの場合、次のようになります。

$$

$$\ left（\ begin {array} {ccccc} f（-1、-1）＆f \ left（-\ frac {1} {2}、-1 \ right）＆f（0、-1）＆f \左（\ frac {1} {2}、-1 \右）＆f（1、-1）\\ f \左（-1、-\ frac {1} {2} \右）＆f \左（-\ frac {1} {2}、-\ frac {1} {2} \ right）＆f \ left（0、-\ frac {1} {2} \ right）＆f \ left（\ frac { 1} {2}、-\ frac {1} {2} \右）＆f \左（1、-\ frac {1} {2} \右）\\ f（-1.0）＆f \左（-\ frac {1} {2}、0 \ right）＆f（0,0）＆f \ left（\ frac {1} {2}、0 \ right）＆f（1,0）\\ f \左（-1、\ frac {1} {2} \右）＆f \左（-\ frac {1} {2}、\ frac {1} {2} \右）＆f \左（0、 \ frac {1} {2} \ right）＆f \ left（\ frac {1} {2}、\ frac {1} {2} \ right）＆f \ left（1、\ frac {1} {2 } \ right）\\ f（-1,1）＆f \ left（-\ frac {1} {2}、1 \ right）＆f（0,1）＆f \ left（\ frac {1} { 2}、1 \右）＆f（1,1）\\ \ end {array} \ right）$$

または、まだゼロである境界値を除外すると、座標は式によって計算されます

$$

$$\ frac {2 index-size + 1} {size}$$

マトリックスはそれに応じて次の形式を取ります

$$

$$\ left（\ begin {array} {ccccc} f \ left（-\ frac {4} {5}、-\ frac {4} {5} \ right）＆f \ left（-\ frac {2} { 5}、-\ frac {4} {5} \右）＆f \左（0、-\ frac {4} {5} \右）＆f \左（\ frac {2} {5}、-\ frac {4} {5} \ right）＆f \ left（\ frac {4} {5}、-\ frac {4} {5} \ right）\\ f \ left（-\ frac {4} {5 }、-\ frac {2} {5} \ right）＆f \ left（-\ frac {2} {5}、-\ frac {2} {5} \ right）＆f \ left（0、-\ frac {2} {5} \ right）＆f \ left（\ frac {2} {5}、-\ frac {2} {5} \ right）＆f \ left（\ frac {4} {5}、 -\ frac {2} {5} \ right）\\ f \ left（-\ frac {4} {5}、0 \ right）＆f \ left（-\ frac {2} {5}、0 \ right ）＆f（0,0）＆f \ left（\ frac {2} {5}、0 \ right）＆f \ left（\ frac {4} {5}、0 \ right）\\ f \ left（ -\ frac {4} {5}、\ frac {2} {5} \右）＆f \左（-\ frac {2} {5}、\ frac {2} {5} \右）＆f \左（0、\ frac {2} {5} \右）＆f \左（\ frac {2} {5}、\ frac {2} {5} \右）＆f \左（\ frac {4} {5}、\ frac {2} {5} \右）\\ f \左（-\ frac {4} {5}、\ frac {4} {5} \右）＆f \左（-\ frac {2} {5}、\ frac {4} {5} \右）＆f \左（0、\ frac {4} {5} \右）＆f \左（\ frac {2} {5}、 \ frac {4} {5} \ right）＆f \ left（\ frac {4} {5}、\ frac {4} {5} \ right）\\ \ end {array} \ right）$$

マトリックス要素が式によって計算された後、それらの合計を計算し、マトリックスをそれに分割する必要があります。 たとえば、行列を取得する場合

$$

$$\左（\ begin {array} {ccc} 1＆4＆1 \\ 4＆20＆4 \\ 1＆4＆1 \\ \ end {array} \ right）$$

すべての要素の合計は40になり、正規化後は次の形式になります

$$

$$\左（\ begin {array} {ccc} \ frac {1} {40}＆\ frac {1} {10}＆\ frac {1} {40} \\ \ frac {1} {10}＆\ frac {1} {2}＆\ frac {1} {10} \\ \ frac {1} {40}＆\ frac {1} {10}＆\ frac {1} {40} \\ \ end {array } \右）$$

すべての要素の合計が1になります。

線形減衰

開始するには、次の最も単純な関数を使用します。

$$

$$\ left \ {\ begin {array} {ll} 1-x、＆x <1 \\ 0、＆x \ geqslant 1 \\ \ end {array} \ right。$$

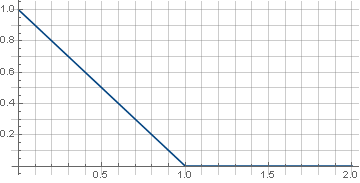
ここでの区分的連続定義では、関数がゼロになることが保証され、回転中に行列の角にアーチファクトがないことが必要です。 さらに、回転は常に正の座標の平方和のルートを使用するため、値の正の部分でのみ関数を決定すれば十分です。 その結果、以下が得られます。

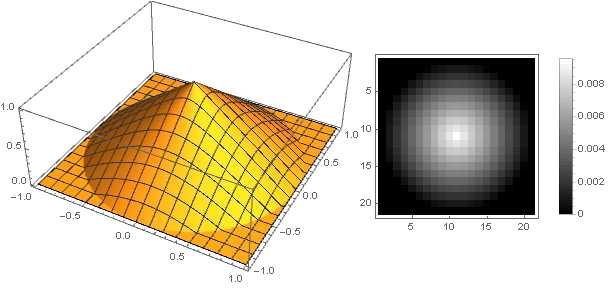
ソフト線形減衰

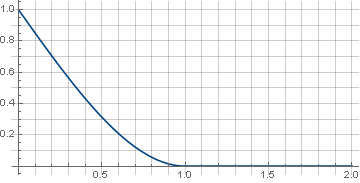
斜線からゼロ関数への急激な移行は、美意識との矛盾を引き起こす可能性があります。 これを解決するには、関数が役立ちます。

$$

$$1- \ frac {n x-x ^ n} {n-1}$$

その中で $$$n$ ドッキングの「剛性」を決定し、 $$$n> 1$ 。 例えば $$$n = 3$ 私たちは得る

$$

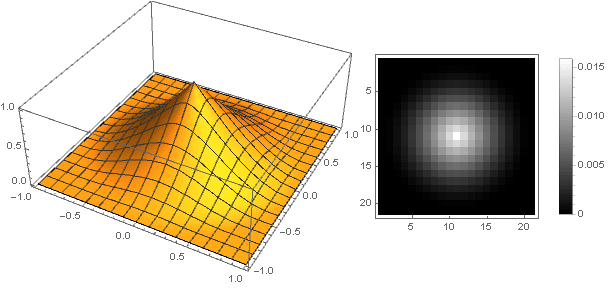
$$\左\ {\ begin {array} {ll} 1- \ frac {3 xx ^ 3} {2}、＆x <1 \\ 0、＆x \ geqslant 1 \\ \ end {array} \右。$$

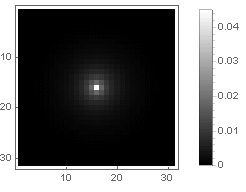
フィルター自体は次のようになります

双曲線減衰

別の関数（双曲線など）を使用して、フィルターをより「シャープ」にし、より滑らかにゼロにすることができます。







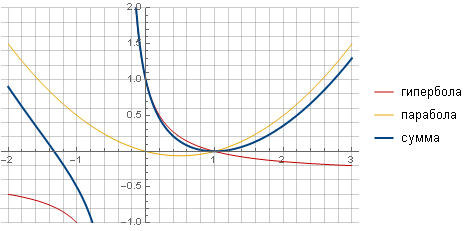
すべての計算と簡略化の後、式を取得します

$$

$$\ left \ {\ begin {array} {ll} \ frac {（x-1）^ 2（k x + k + 1）} {（k + 1）（k x + 1）}、＆x <1 \\ 0、＆x \ geqslant 1 \\ \ end {array} \ right。$$

どのパラメータ $$$k> 0$ 減衰の性質を決定します。







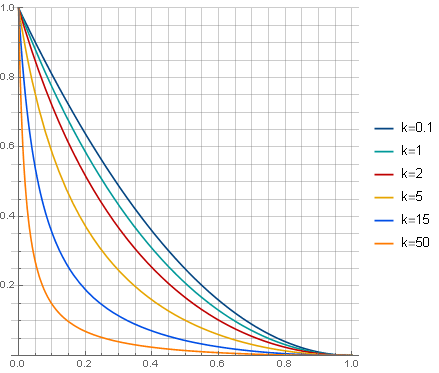
フィルター自体は（ $$$k = 5$ ）方法

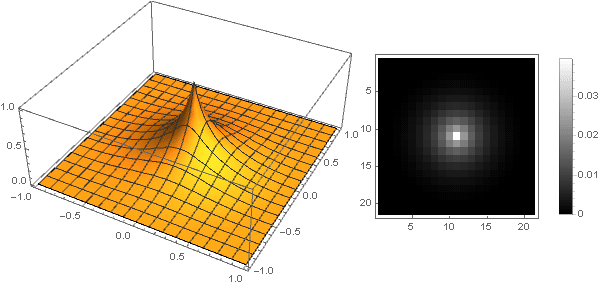
ボケ効果

別の方法を使用することもできます-フィルターの上部をシャープではなく、愚かにします。 これを実装する最も簡単な方法は、減衰関数を定数として設定することです。

$$

$$\ left \ {\ begin {array} {ll} 1、＆x <1 \\ 0、＆x \ geqslant 1 \\ \ end {array} \ right。$$

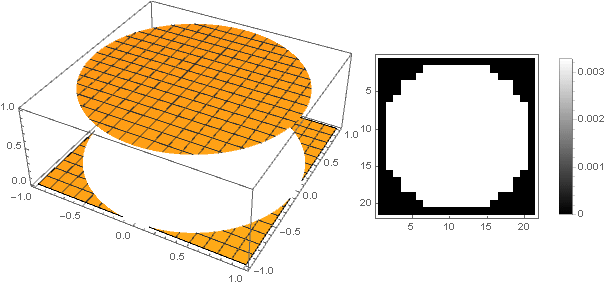
しかし、この場合、私たちは美の感覚とは対照的な強いピクセル化を取得します。 エッジでより滑らかにするために、高次の放物線が役立ちます。そこから、縦座標軸に沿って移動し、二乗することにより、

$$

$$\ left \ {\ begin {array} {ll} \ left（1-x ^ n \ right）^ 2、＆x <1 \\ 0、＆x \ geqslant 1 \\ \ end {array} \ right。$$

さまざまなパラメーター $$$n$ 幅広いフィルターオプションを取得できます。

$$

$$n = 0.5$$

$$

$$n = 2$$

$$

$$n = 10$$

$$

$$n = 50$$

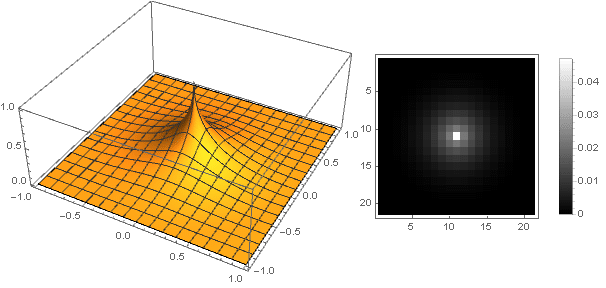
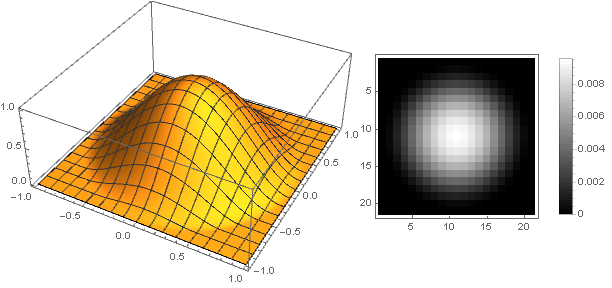
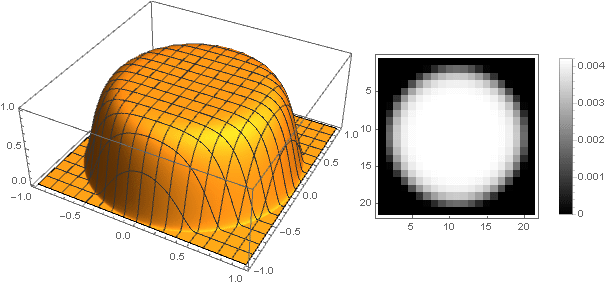
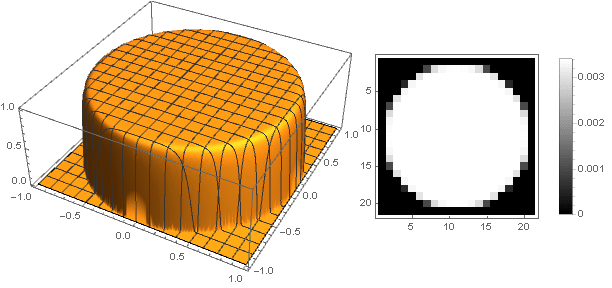
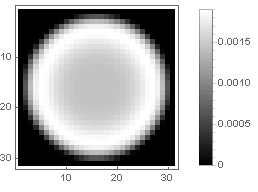
そして、減衰機能をわずかに変更することにより、フィルターの端にあるリングを、たとえば次のように、よりはっきりさせることができます。

$$

$$\ left \ {\ begin {array} {ll} \ left（1-x ^ n \ right）^ 2 \ left（d + x ^ m \ right）、＆x <1 \\ 0、＆x \ geqslant 1 \\ \ end {array} \ right。$$

ここパラメータ $$$d$ 中心の高さを決定し、 $$$m$ -エッジへの移行のシャープネス。

のために $$$d = 0.2、m = 2、n = 10$ 私たちは得る







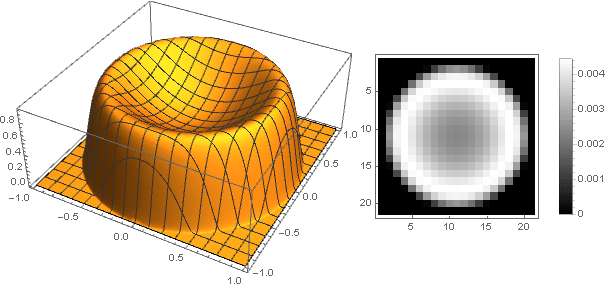
でも $$$d = 0、m = 12、n = 2$

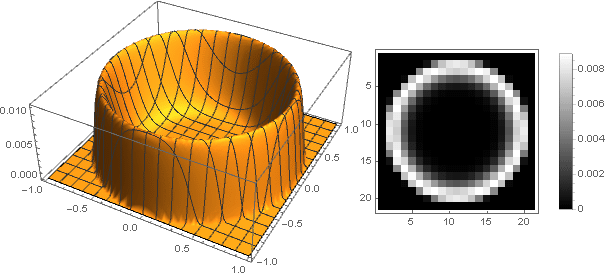
ガウスバリエーション

ガウス関数自体の機能も直接変更できます。 これを行う最も明白な方法は、指数をパラメータ化することです。今は考慮しませんが、より興味深いオプションを使用します。

$$

$$\ left \ {\ begin {array} {ll} e ^ {\ frac {kx ^ 2} {x ^ 2-1}}、＆-1 <x <1 \\ 0、その他\\ \ end {配列} \右$$

という事実のために $$$x$ 単位分母 $$$x ^ 2-1$ 端数がゼロになる傾向がある $$$\ frac {k x ^ 2} {x ^ 2-1}$ はマイナスの無限大になる傾向があり、指数自体もゼロになる傾向があります。 したがって、 $$$x ^ 2-1$ で関数定義ドメインを圧縮できます $$$（-\ infty、\ infty）$ 前に $$$（-1,1）$ 。 また、 $$$x = \ pm 1$ ゼロ除算による（ $$$1 ^ 2-1 = 0$ ）関数の値は定義されていませんが、2つの制限があります-一方（内側から）の制限はゼロで、もう一方は無限です：

$$

$$\ underset {x \ to 1 ^-} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = 0$$

$$

$$\ underset {x \ to 1 ^ +} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = \ infty$$

境界値は間隔に含まれていないため、片側の制限のゼロだけで十分です。 興味深いことに、このプロパティはこの関数のすべての導関数に拡張され、ゼロとの完全な一致を保証します。



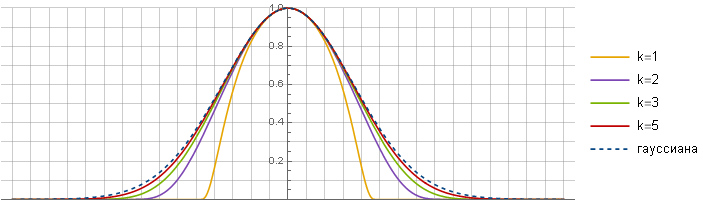
パラメータ $$$k$ ガウス分布との類似性を決定します-大きくなるほど、類似性がより強くなります-線形セクションが増加するため $$$\ frac {1} {x ^ 2-1}$ 関数の中心に落ちます。 このため、限界では、元のガウスを取得できると仮定できますが、残念ながら、いいえ、関数はまだ異なります。







今、あなたは何が起こったのかを見ることができます：

$$

$$k = 5$$

$$

$$k = 2$$

$$

$$k = 0.5$$

$$

$$k = 0.1$$

$$

$$k = 0.01$$

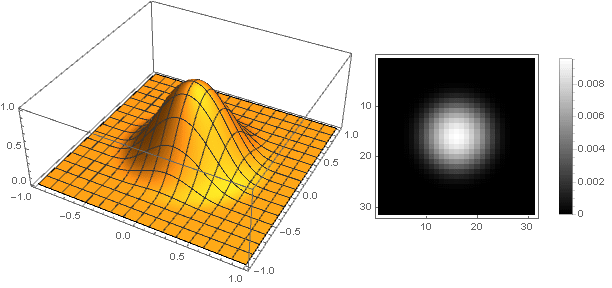
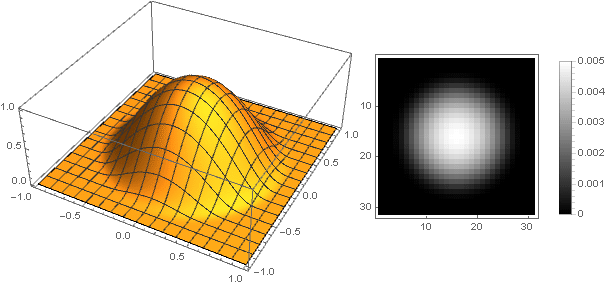
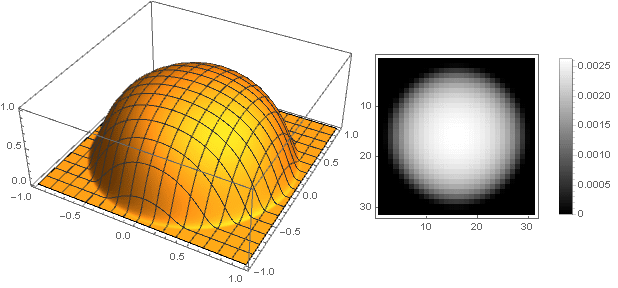
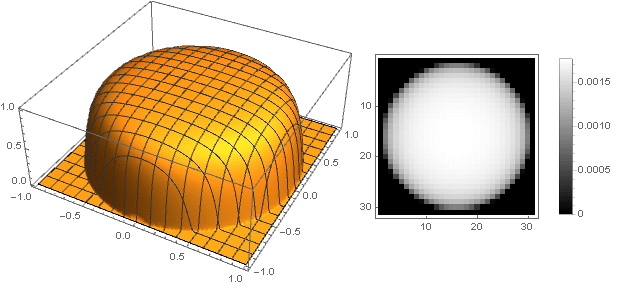
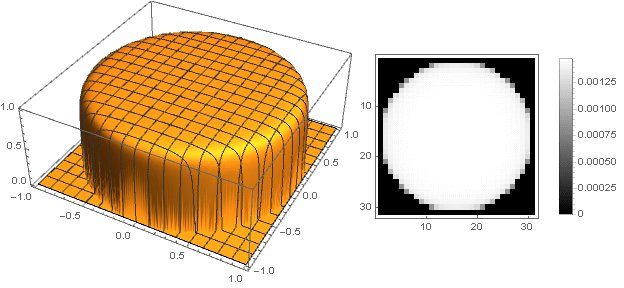
形状バリエーション

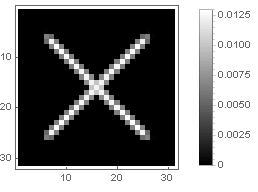
遷移関数を2つの座標から1つの座標に変更することにより $$$\ sqrt {x ^ 2 + y ^ 2}$ 、ディスクだけでなく他の形状を取得できます。 例：

$$

$$f \ left（\ frac {\ left | x-y \ right | + \ left | x + y \ right |} {2} \ right）$$

$$

$$f（\左| x \右| + \左| y \右|）$$

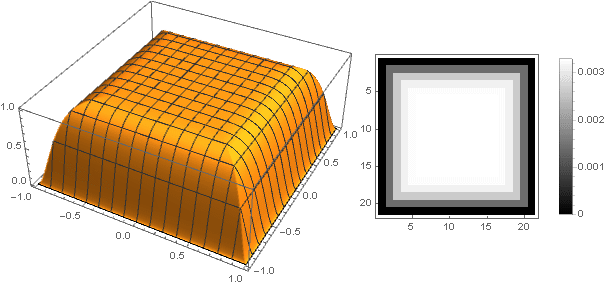
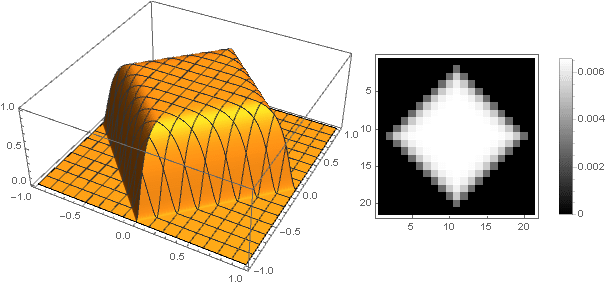
複素数に移動すると、より複雑な図を作成できます。

$$

$$f \ left（\ frac {\ left | \ Re \ left（（x + iy）（-1）^ {\ frac {0} {3}} \ right）\ right | + \ left | \ Re \ left （（x + iy）（-1）^ {\ frac {1} {3}} \ right）\ right | + \ left | \ Re \ left（（x + iy）（-1）^ {\ frac { 2} {3}} \右）\右|} {\ sqrt {3}} \右）$$

$$

$$f \ biggl（10 \左| \ Re \左（（x + iy）（-1）^ {\ frac {1} {8}} \右）\右| \ biggr）\ cdot f（\左| x + iy \右|）$$

$$

$$f \ biggl（\ biggl | 5 \ left | x + iy \ right |（x + iy）\ Re \ biggl（\ cos \ left（\ frac {5} {2} \ arg（x + iy）\ right ）\ biggr）\ biggr | \ biggr）\ cdot f（\左| x + iy \右|）$$

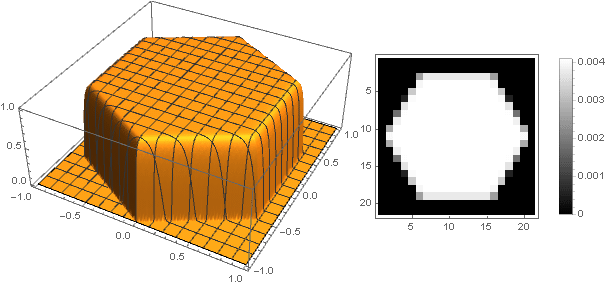
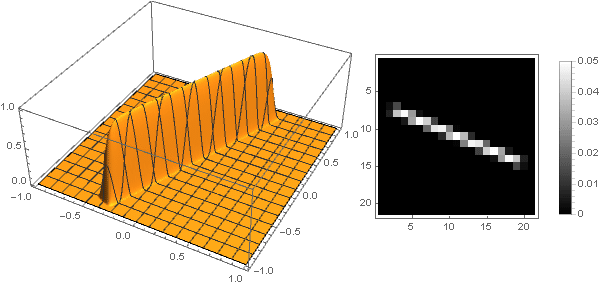
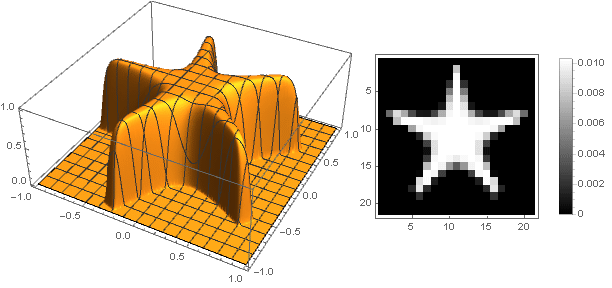
この場合、座標を変換するときに間隔を超えないようにする必要があります $$$（0,1）$ -まあ、またはその逆で、引数の負の値に対して減衰関数を再定義します。

いくつかの具体的な例

記事は、特定の画像での実用的なテストなしでは完成しません。 科学的な仕事がないので、 レナのイメージも取りません。柔らかくてふわふわしたものを取ります。





































同じフィルターですが、テキストの場合：

おわりに

同様に、シャープ化やアウトライン付きのフィルターなど、より複雑なフィルターを作成できます。 また、すでに考慮されているものを変更します。



フィルター係数の値が座標または直接フィルター処理される画像に依存する場合、非線形フィルター処理も特に重要ですが、これはすでに他の研究の対象です。



より詳細には、定数とドッキングするための関数の派生をここで検討します 。 ここで検討するウィンドウ関数は減衰関数としても使用できます-引数c（0,1）を（ $$$\ frac {1} {2}$ 、1）または最初に式によってウィンドウ関数を考慮する $$$\ frac {1} {2} \ left（f \ left（\ frac {t x + 1} {t-1} \ right）-f \ left（\ frac {t x-1} {t-1} \右）\右）$ 。



この記事のWolfram Mathematicaソース文書はこちらからダウンロードできます 。