
00年代後半のボードゲームの本当のブームの後、ゲームの入ったいくつかの箱が家族の中に残った。 それらの1つは、元のドイツ語版のゲーム「Hare and Hedgehog」です。 ランダム性の要素が最小化された数人のプレーヤー向けのゲームで、落ち着いた計算と数ステップで「先読み」するプレーヤーの能力が勝ちます。
ゲームで頻繁に敗北したため、コンピューターの「インテリジェンス」を書いて最高の動きを選択しました。 知能、理想的にはうさぎとハリネズミのグランドマスターと戦うことができます(そして、チェスではなくお茶、ゲームが簡単になります)。 記事の残りの部分では、開発プロセス、AIロジック、およびソースへのリンクについて説明します。
ゲームのルールHare and Hedgehog
65セルの競技場には、2〜6人の参加者からなる複数のプレーヤーチップがあります(もちろん、ドローイング、非正規、外見、まあまあ)。
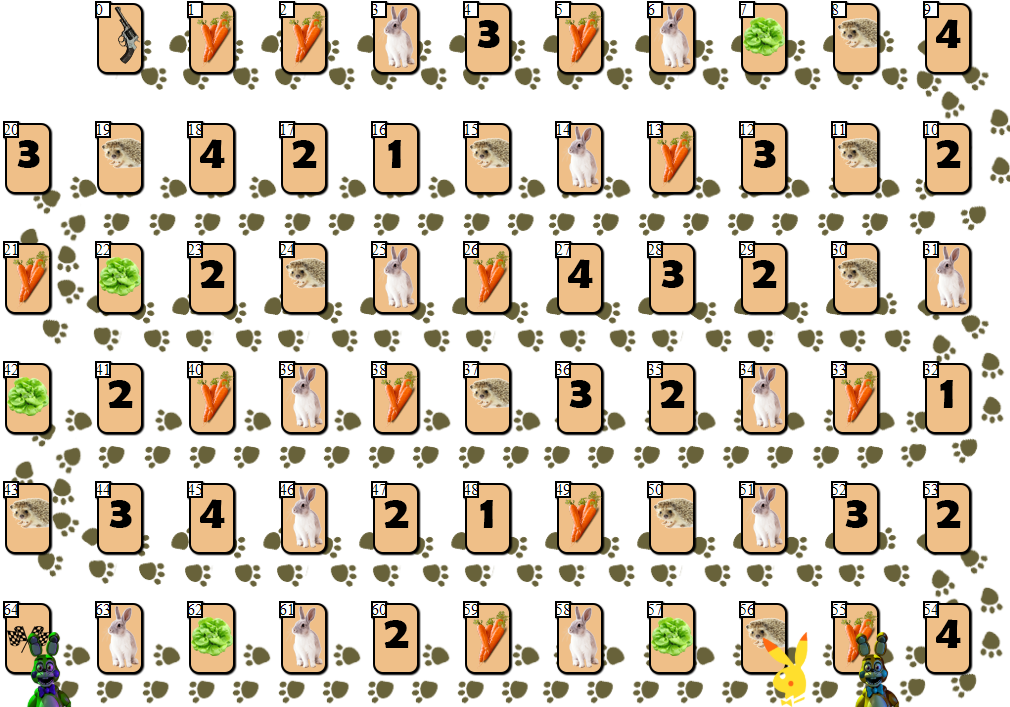
インデックス0(開始)および64(終了)のセルを除き、各セルに配置できるプレーヤーは1人だけです。 各プレイヤーの目標は、ライバルに先んじてフィニッシュセルに進むことです。
前進するための「燃料」はニンジン、つまりゲーム通貨です。 開始時に、各プレイヤーは68個のニンジンを受け取ります。
ニンジンに加えて、プレーヤーは最初に3枚のサラダカードを受け取ります。 サラダは特別な「アーティファクト」であり、プレイヤーはフィニッシュの前に取り除く必要があります 。 サラダを取り除きます(これは、次のような特別なサラダケージでのみ行うことができます:

)を含むプレーヤーは、追加のニンジンを受け取ります。 その前に、あなたの動きをスキップします。 カードを離れるサラダの前にいるプレーヤーが多いほど、プレーヤーが受け取るニンジンが多くなります:10 x(他のプレーヤーに対するフィールドでのプレーヤーの位置)。 つまり、2番目のフィールドに立っているプレイヤーは20個のニンジンを受け取り、サラダのケージを離れます。
プレーヤーの位置がセルの番号と一致する場合、レタスのセルと同様に、番号1から4のセルは数十のニンジンをもたらすことができます(1から4、番号1のセルはフィールドの4番目と6番目の位置にも適しています)。
プレイヤーは、ニンジンのイメージが付いたケージに残り、このアクションのために10個のニンジンを受け取るか与えることができます。 なぜプレイヤーは「燃料」を与えなければならないのですか? 実際には、プレーヤーは最後の移動後に10個のニンジンしか持てないということです(2番目を終えると20、3番目を終えると30など)。
最後に、プレーヤーは、 最も近い無料のハリネズミでNステップを踏むことで10 x Nのニンジンを得ることができます(最も近いハリネズミが忙しい場合、そのような移動は不可能です)。
次の式に従って、移動のコストは移動の数に比例せずに計算されます(切り上げ):
、
ここで、Nは前方へのステップ数です。
したがって、1つのセルを進めるために、プレーヤーは1つのニンジン、2つのセルに3つのニンジン、3つのセルに6つのニンジン、4に10、...、20のセルを進めるために210のニンジンを与えます。
最後のセル-うさぎの絵のあるセル-は、ランダム性の要素をゲームに導入します。 ウサギのいるケージの上に立って、プレーヤーはパイルから特別なカードを引き、その後いくつかのアクションが実行されます。 カードとゲームの状況に応じて、プレーヤーはニンジンを失ったり、余分なニンジンを入手したり、1ターンスキップしたりする場合があります。 「効果」のあるカードの中には、プレーヤーにとってより多くのネガティブなシナリオがいくつかあり、ゲームが慎重に計算されることを奨励しています。
AIを使用しない実装
ゲームの「インテリジェンス」の開発の基礎となる最初の実装では、各プレイヤーが人を動かすという選択肢に限定していました。
ゲームをクライアントとして実装することにしました。静的な1ページのWebサイトで、その「ロジック」はすべてJSに実装され、サーバーはWEB APIアプリケーションです。 サーバーは.NET Core 2.1で記述され、Windows / Linux / Mac OSで実行できるdllファイルという1つのアセンブリアーティファクトを生成します。
クライアント部分の「ロジック」は最小限に抑えられます(GUIは純粋に実用的なため、UXも同様です)。 たとえば、Webクライアントはチェック自体を実行しません-プレーヤーによって要求されたルールが許可されているかどうか。 このチェックはサーバーで実行されます。 サーバーは、プレイヤーに現在のゲーム位置から何ができるかをクライアントに伝えます。
サーバーは、古典的なムーアマシンです。 サーバーロジックには、「接続されたクライアント」、「ゲームセッション」などの概念がありません。
サーバーは、受信した(HTTP POST)コマンドを処理するだけです。 「コマンド」パターンはサーバーに実装されています。 クライアントは、次のコマンドのいずれかの実行を要求できます。
- 新しいゲーム、つまり 指定された人数のチップを「クリーン」ボードに「配置」する
- コマンドに示された移動を行います
2番目のチームの場合、クライアントはサーバーに現在のゲーム位置(Dispositionクラスのオブジェクト)、つまり次の形式の説明を送信します。
- 位置、各うさぎのニンジンとレタスの数、さらにうさぎが順番を逃していることを示す追加のブールフィールド
- 移動するウサギのインデックス。
サーバーは、追加情報を送信する必要はありません-例えば、競技場に関する情報。 チェスのスケッチを記録するように、ボード上の黒と白のセルの配置をペイントする必要はありません-この情報は定数として扱われます。
応答として、サーバーはコマンドが正常に完了したかどうかを示します。 技術的には、クライアントは、たとえば、無効な移動を要求する場合があります。 または、1人の参加者のために新しいゲームを作成してみてください。これは明らかに意味がありません。
チームが成功した場合、応答には、新しいゲームの位置と、キュー内の次のプレイヤーが行うことができる移動のリスト(新しい位置の現在)が含まれます。
これに加えて、サーバー応答にはいくつかのサービスフィールドが含まれます。 たとえば、ウサギのカードのテキストは、対応するケージのステップでプレイヤーによって「引き出された」。
プレイヤーターン
プレーヤーのターンは整数としてエンコードされます:
- 0、プレイヤーが現在の広場に留まることを余儀なくされた場合、
1、2、... Nは1、... Nは前進、 - -1、-2、... -Mは1〜M個のセルを最も近い自由なハリネズミに戻します。
- 1001、1002-ニンジンセルにとどまり、このために10個のニンジンを受け取る(1001)または与える(1002)ことを決定したプレーヤーの特別なコード。
ソフトウェア実装
サーバーは、要求されたコマンドのJSONを受信し、対応する要求クラスの1つに解析して、要求されたアクションを実行します。
クライアント(プレーヤー)がチームに転送されたポジション(POS)からCMDコードを使用して移動を要求した場合、サーバーは次のアクションを実行します。
- そのような移動が可能かどうかを確認します
- 現在の位置から新しい位置を作成し、それに対応する修正を適用し、
新しいポジションの多くの可能な動きを取得します。 移動するプレーヤーのインデックスは、 位置を説明するオブジェクトに既に含まれていることを思い出させてください。 - 新しい位置、可能な移動、またはfalseに等しい成功フラグ、およびエラーの説明を含む応答をクライアントに返します。
要求された移動(CMD)の許容性をチェックし、新しいポジションを構築するロジックは、私たちが望むよりも少し密接に接続されていることが判明しました。 このロジックでは、許容可能な動きを見つける方法に共通点があります。 この機能はすべて、TurnCheckerクラスによって実装されます。
チェック/実行メソッドの入力時に、TurnCheckerはゲーム位置のクラス(Disposition)のオブジェクトを受け取ります。 Dispositionオブジェクトには、プレーヤーデータ(ヘイズ[]ヘイズ)の配列、移動を行うプレーヤーのインデックス+ TurnCheckerオブジェクトの操作中に入力されるサービス情報が含まれます。
競技場は、SingleMapとして実装されるFieldMapクラスを記述します。 このクラスには、セルの配列と後続の計算を簡素化/高速化するために使用されるオーバーヘッド情報が含まれています。
パフォーマンスに関する考慮事項
TurnCheckerクラスの実装では、ループを回避するために、可能な限り試みました。 実際、一連の許容される移動/移動の実行を取得するメソッドは、準最適な移動の検索手順中に数千(数万)回呼び出されます。
したがって、たとえば、次の式を使用して、プレーヤーがN個のニンジンを使用して前進できるセルの数を計算します。
セルiがプレイヤーの1人によって占有されているかどうかを確認し、プレイヤーのリストをたどりません(このアクションはおそらく何度も実行する必要があるためです)が、事前に入力された[cell_index、busy_cage_ flag]という形式の辞書に目を向けます。
指定されたハリネズミのセルが、プレーヤーが占有している現在のセルに最も近い(背後にある)かどうかを確認するとき、要求された位置を[cell_index、nearest_back_dezh] _index]形式の辞書の値と比較します。
したがって、たとえば、次の式を使用して、プレーヤーがN個のニンジンを使用して前進できるセルの数を計算します。
return ((int)Math.Pow(8 * N + 1, 0.5) - 1) / 2;
セルiがプレイヤーの1人によって占有されているかどうかを確認し、プレイヤーのリストをたどりません(このアクションはおそらく何度も実行する必要があるためです)が、事前に入力された[cell_index、busy_cage_ flag]という形式の辞書に目を向けます。
指定されたハリネズミのセルが、プレーヤーが占有している現在のセルに最も近い(背後にある)かどうかを確認するとき、要求された位置を[cell_index、nearest_back_dezh] _index]形式の辞書の値と比較します。
AIによる実装
サーバーによって処理されるコマンドのリストに1つのコマンドが追加されます。プログラムによって選択された準最適な移動を実行します。 このコマンドは、「プレイヤーの移動」コマンドを少し修正したもので、実際には移動フィールド( CMD )は削除されています。
頭に浮かぶ最初の決定は、発見的手法を使用して「可能な限り最良の」動きを選択することです。 チェスとの類推により、このポジションに何らかのレーティングを設定することで、ムーブで得られた各ゲームポジションを評価できます。
発見的位置評価
たとえば、チェスでは、評価を行うのは非常に簡単です(開口部の荒野に登ることなく):少なくとも、3ポーンの騎士/ビショップの値、ルーク5のポーン、クイーン9、およびキングintの値を取ることにより、ピースの合計「コスト」を計算できます.MaxValueポーン。 推定値を改善するのは簡単です。たとえば、それに追加する(補正係数-係数/指数または他の関数を使用):
- 現在の位置からの可能な動きの数、
- 敵のフィギュアに対する脅威の比率/敵からの脅威。
マットの位置に特別な評価が与えられます。チェックメイトがコンピューターを置いた場合はint.MaxValue 、チェックメイトが人を置いた場合はint.MinValueです。
チェスプロセッサに次の動きを選択するように命じた場合、そのような評価のみに基づいて、プロセッサはおそらく最悪の動きを選択しません。 特に:
- 大きな作品やチェックメイトを取る機会をお見逃しなく、
- ほとんどの場合、コーナーの数字を動かしませんが、
- 数値に打撃を与えることはありません(評価で脅威の数を考慮すると)。
もちろん、そのようなコンピューターの動きは、わずかな意味で動きをする相手との成功のチャンスを彼に残しません。 コンピューターはプラグを無視します。 さらに、彼はおそらくクイーンをポーンと交換することをheしません。
それにもかかわらず、チェスの現在のプレー位置のヒューリスティック評価のアルゴリズム(チャンピオンプログラムの栄冠を主張することなく)は、非常に透明です。 あなたはゲームHare and Hedgehogについて言うことはできません。
一般的な場合、Hare and the Hedgehogのゲームでは、かなりぼやけた格言が機能します。「 ニンジンを増やしてレタスを減らして、さらに先に進む方が良い 」。 ただし、すべてがそれほど簡単ではありません。 たとえば、プレイヤーがゲームの途中でサラダカードを1枚持っている場合、このオプションは非常に有効です。 しかし、サラダカードでフィニッシュラインに立っているプレーヤーは、明らかに負けている状態になります。 評価アルゴリズムに加えて、駒への脅威がチェスの位置のヒューリスティック評価でカウントできるのと同じように、さらに一歩踏み込む機会を得たいと思います。 たとえば、前のプレーヤーの数を考慮して、レタスセル/ポジションセル(1〜4)を離れるプレーヤーが受け取るニンジンのボーナスを考慮する価値があります。
関数として最終グレードを導きました:
E = Ks * S + Kc * C + Kp * P、
ここで、S、C、Pはサラダカード(S)とプレイヤーの手にあるニンジン©を使用して計算されたグレードであり、Pは移動距離にわたってプレイヤーに与えられるスコアです。
Ks、Kc、Kpは対応する補正係数です(これらについては後で説明します)。
最も簡単な方法は、移動したパスのマークを決定することです:
P = i * 3、ここでiはプレーヤーが配置されているセルのインデックスです。
C(ニンジン)のグレーディングはすでに難しくなっています。
特定のC値を取得するには、3つの関数のいずれかを選択します 1つの引数(手のニンジンの数)から。 関数Cのインデックス([0、1、2])は、競技場でのプレーヤーの相対的な位置によって決まります。
- [0]プレーヤーが競技場の半分未満を完了した場合、
- [2]プレイヤーが終了するのに十分な(mb、さらには豊富な)ニンジンを持っている場合、
- [1]その他の場合。
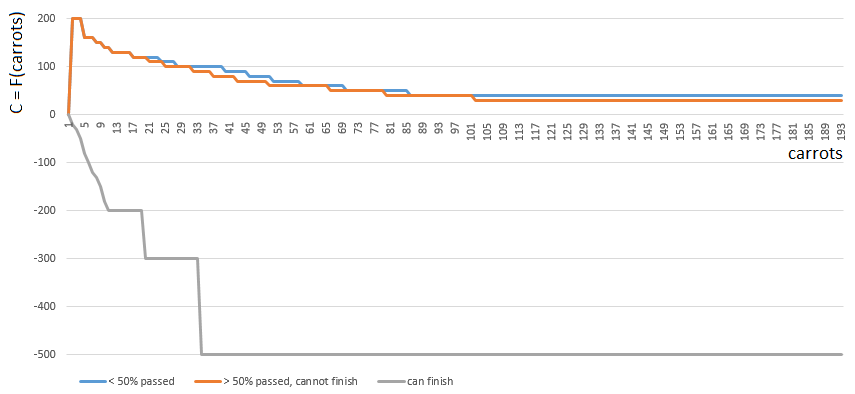
機能0と1は似ています。プレーヤーの手にあるニンジンの「値」は、手のニンジンの数が増えると徐々に減少します。 ゲームはめったにPlyushkinsを奨励しません。 ケース1(渡されたフィールドの半分)では、ニンジンの値は少し速く減少します。
反対に、機能2(プレーヤーは終了できます)は、プレーヤーの手の各ニンジンに大きな罰金(負の係数値)を課します。ニンジンが多いほど、ペナルティ係数が大きくなります。 にんじんが過剰であるため、ゲームのルールによりフィニッシュは禁止されています。
プレーヤーの手のニンジンの量を計算する前に、レタスのセル/セル番号1からのターンあたりのニンジンを考慮して指定します... 4。
「 レタス 」グレードSも同様の方法で推定されます。 プレーヤーの手のサラダの量(0〜3)に応じて、機能が選択されます または 。 関数の引数 。 -再び、プレーヤーが移動した「相対」パス。 つまり、サラダが前面に残っているセルの数(プレーヤーが占有しているセルに対して):
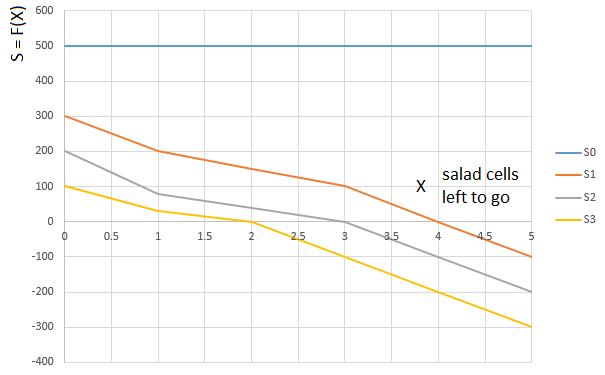
曲線 -レタスの手札が0枚のプレーヤーの場合、プレーヤーの前のレタス細胞の数(0〜5)の評価関数(S)、
曲線 -1枚のサラダカードを手に持っているプレーヤーなどと同じ機能
したがって、最終評点(E = Ks * S + Kc * C + Kp * P)では、以下が考慮されます。
- プレイヤーが自分の移動の直前に受け取る余分なニンジン
- プレイヤーが移動した経路
- スコアに非線形的に影響する、ニンジンと手のレタスの量。
そして、最大のヒューリスティックスコアを持つ次の動きを選択するコンピューターのプレイ方法を次に示します。
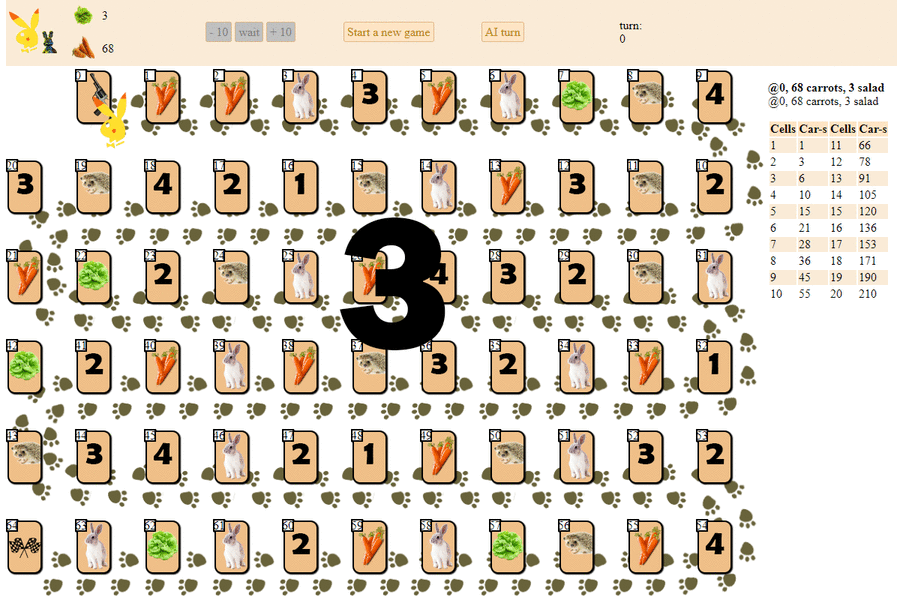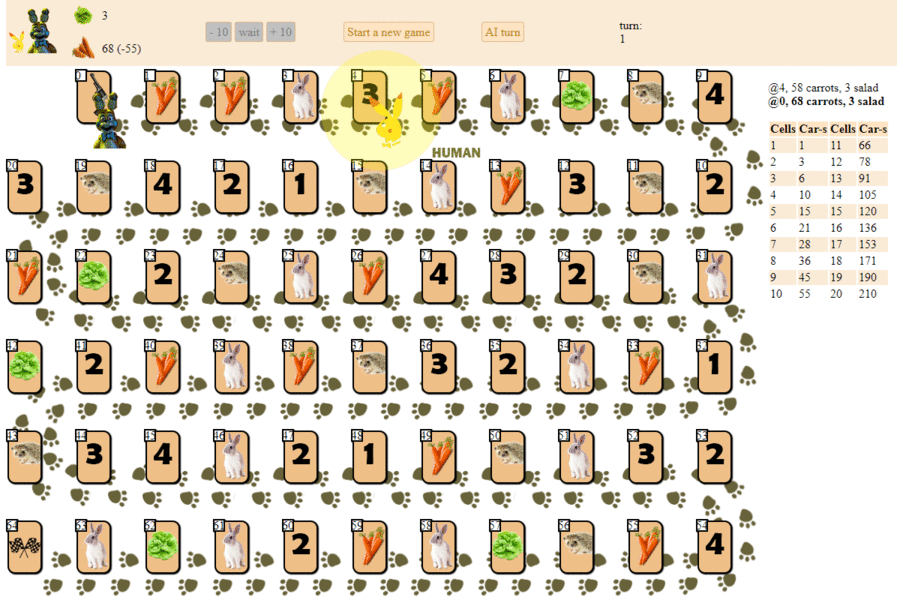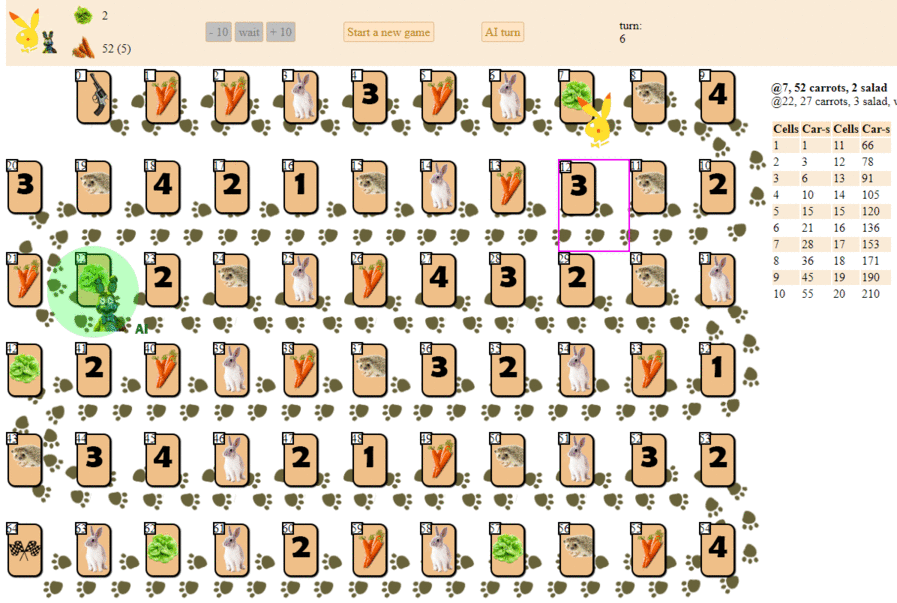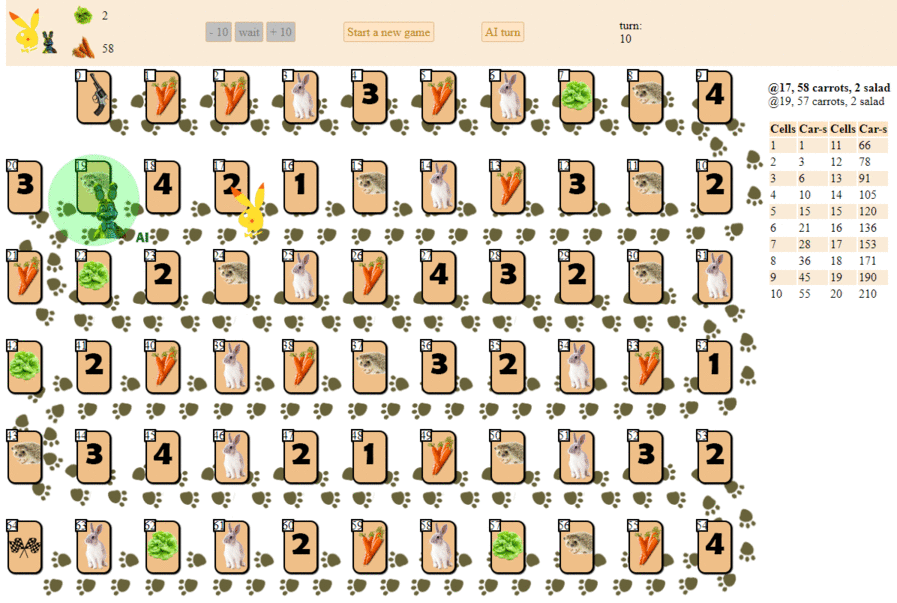
原則として、デビューはそれほど悪くありません。 ただし、このようなAIに良いゲームを期待することはできません:ゲームの途中までに、緑色の「ロボット」は繰り返し動き始め、最後にはハリネズミの前後に動きを数回繰り返し、最終的に終了します。 偶然のせいで、彼はプレーヤーの後ろでフィニッシュします。
実装ノート
推定値の計算は、特別なクラス-EvaluationCalculatorによって管理されます。 ニンジンに相対的な位置を評価するための関数-サラダカードは、計算機クラスの静的コンストラクターの配列にロードされます。 入力時に、位置推定方法は、位置オブジェクト自体とプレーヤーのインデックスを受け取ります。この視点から、アルゴリズムによって位置が評価されます。 つまり、仮想ポイントが考慮されるプレーヤーに応じて、同じゲームの位置が複数の異なる評価を受けることができます。
決定木とミニマックスアルゴリズム
敵対的なミニマックスゲームでは、意思決定アルゴリズムを使用します。 私の意見では、アルゴリズムはこの投稿(翻訳)で説明されています。
私たちは、プログラムにいくつかの動きを「見る」ことを教えます。 現在の位置から(そして、背景はアルゴリズムにとって重要ではありません-プログラムがムーア機として機能することを思い出してください)、番号1の番号が付けられていると仮定すると、プログラムは2つの動きをすることができます。 2つのポジション、2と3を取得します。次に、プレイヤーのターン-人(一般的な場合-敵)が来ます。 2番目の位置から、相手には3つの動きがあり、3番目からは2つの動きしかありません。 次に、再び移動する順番はプログラムに当てはまり、合計で5つの可能な位置から10の移動を行うことができます。
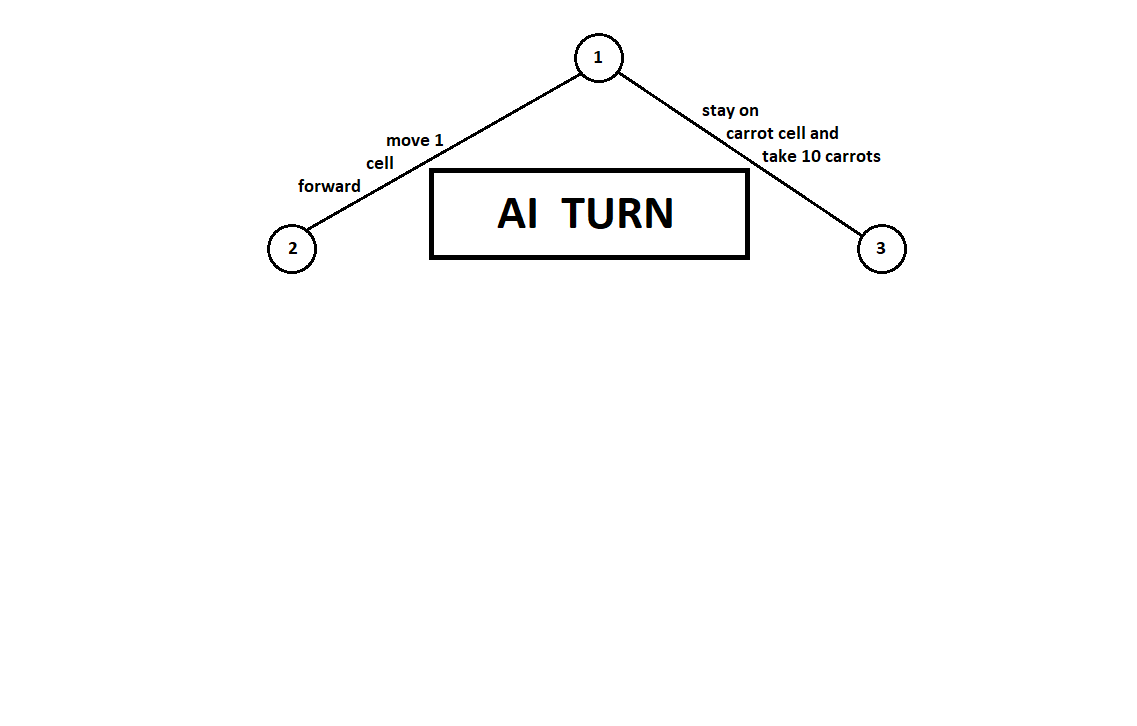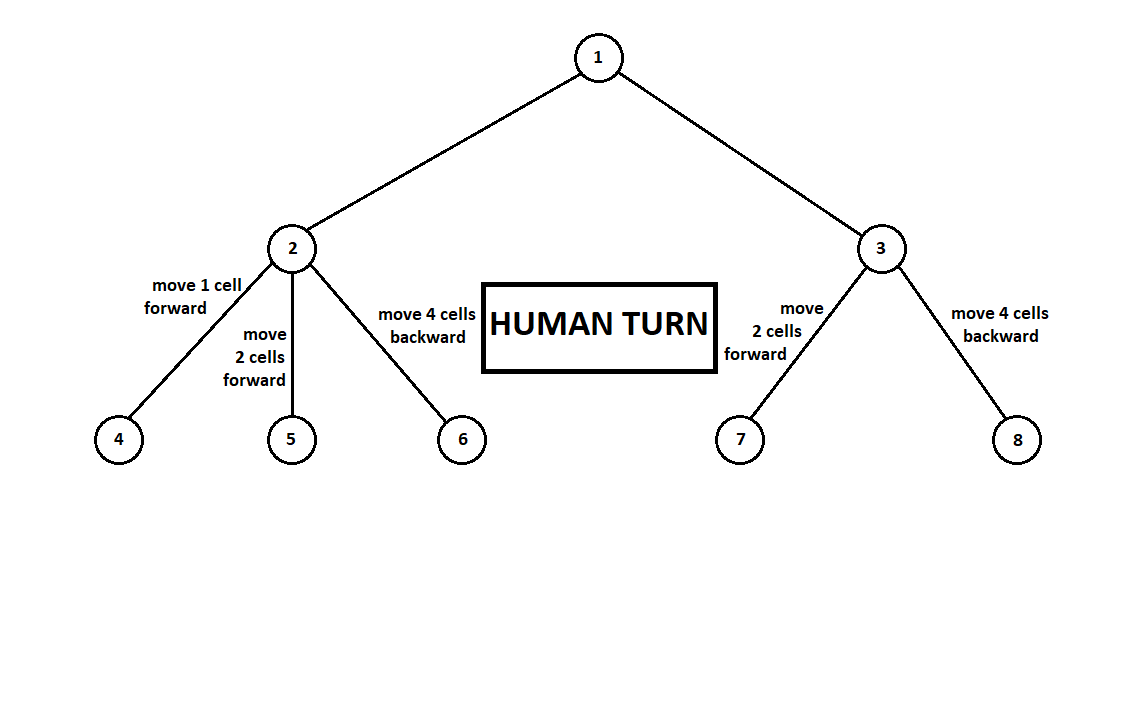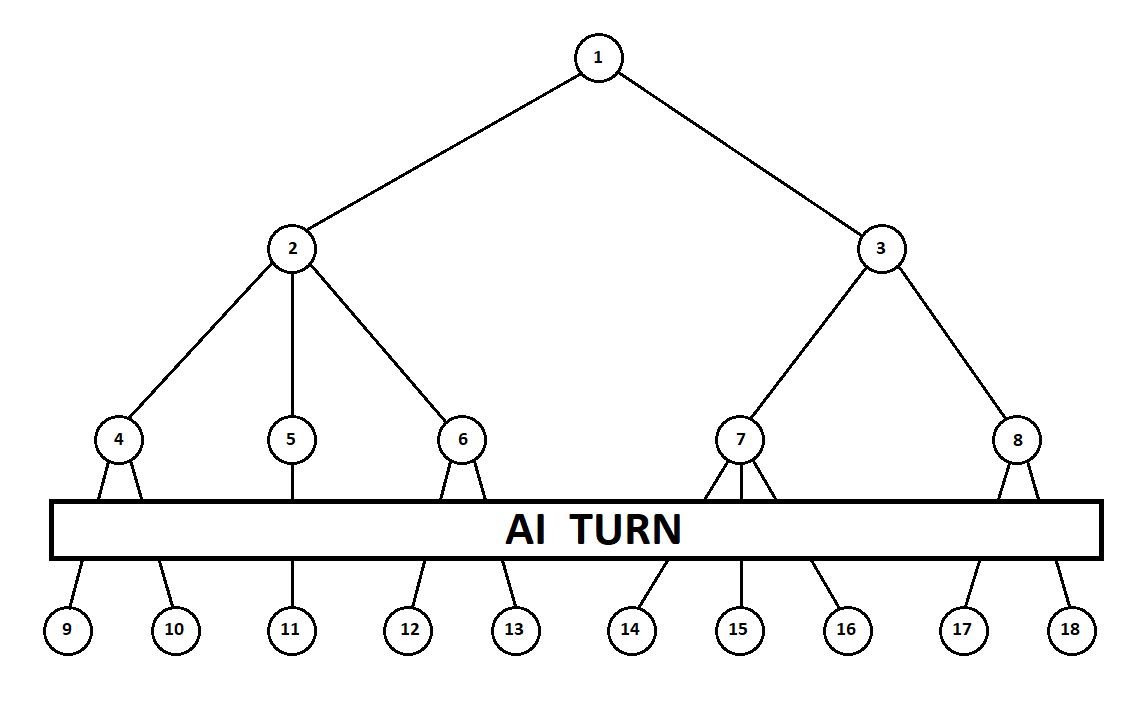
コンピューターの2回目の移動の後、ゲームが終了し、受信した位置のそれぞれが、1番目と2番目のプレーヤーの視点から評価されたとします。 そして、すでに評価アルゴリズムを実装しています。 ベクトルの形で各最終位置(ツリーの葉9 ... 18)を評価しましょう 、
どこで -最初のプレーヤーについて計算されたスコア、 -2番目のプレーヤーのスコア:
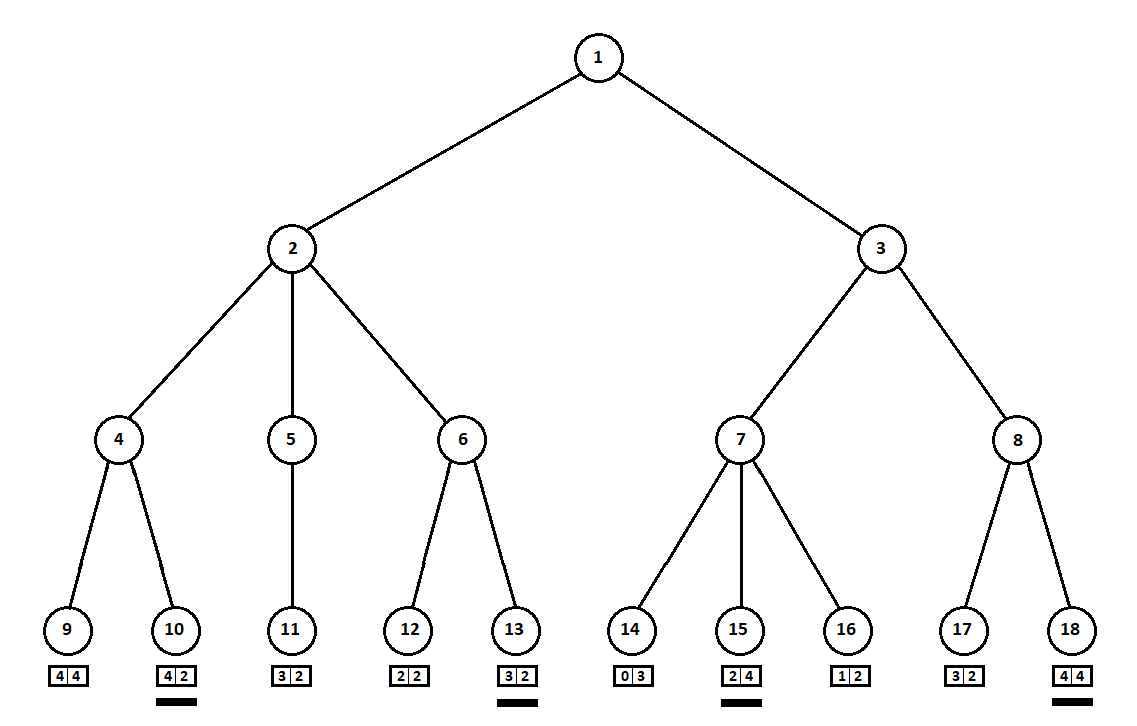
コンピューターは最後の動きをするため、オプション([9、10]、[11]、[12、13]、[14、15、16]、[17、18]の各サブツリー)を選択しますそれは彼に良い評価を与えます。 問題はすぐに発生します。どの原則によって「最良の」ポジションを選択すべきでしょうか。
たとえば、2つの動きがあり、その後に格付け[5; 5]および[2; 1]。 最初のプレーヤーを評価します。 次の2つの選択肢があります。
- i番目のプレーヤーのi番目のスコアの最大絶対値を使用した位置選択。 言い換えれば、競合他社に関係なく、勝利を熱望する高貴なレーサー、レスリー。 この場合、推定値が[5; 5]。
- 競合他社の見積もりと比較して最大の格付けを持つポジションの選択は、敵に汚いトリックを与える機会を逃さないcな教授Faithです。 たとえば、2番目のポジションから開始することを計画しているプレーヤーに故意に遅れをとる場合。 評価のあるアイテム[2; 1]。
私のソフトウェア実装では、グレード選択アルゴリズム(グレードベクトルをi番目のプレーヤーのスカラー値にマッピングする関数)をカスタムパラメーターにしました。 さらなるテストにより、驚くべきことに、最初の戦略の優位性-最大絶対値による位置の選択が示されました 。
ソフトウェア実装の機能
AI(TurnMakerクラス)の設定で最適なグレードを選択する最初のオプションが指定されている場合、対応するメソッドのコードは次の形式になります。
2番目の方法-競合他社の位置に対する最大値-は少し複雑に実装されています。
int ContractEstimateByAbsMax(int[] estimationVector, int playerIndex) { return estimationVector[playerIndex]; }
2番目の方法-競合他社の位置に対する最大値-は少し複雑に実装されています。
int ContractEstimateByRelativeNumber(int[]eVector, int player) { int? min = null; var pVal = eVector[player]; for (var i = 0; i < eVector.Length; i++) { if (i == player) continue; var val = pVal - eVector[i]; if (!min.HasValue || min.Value > val) min = val; } return min.Value; }
選択した推定値(図で下線が引かれている)は、レベルアップに転送されます。 ここで、アルゴリズムが選択する後続の位置を把握して、敵が位置を選択する必要があります。
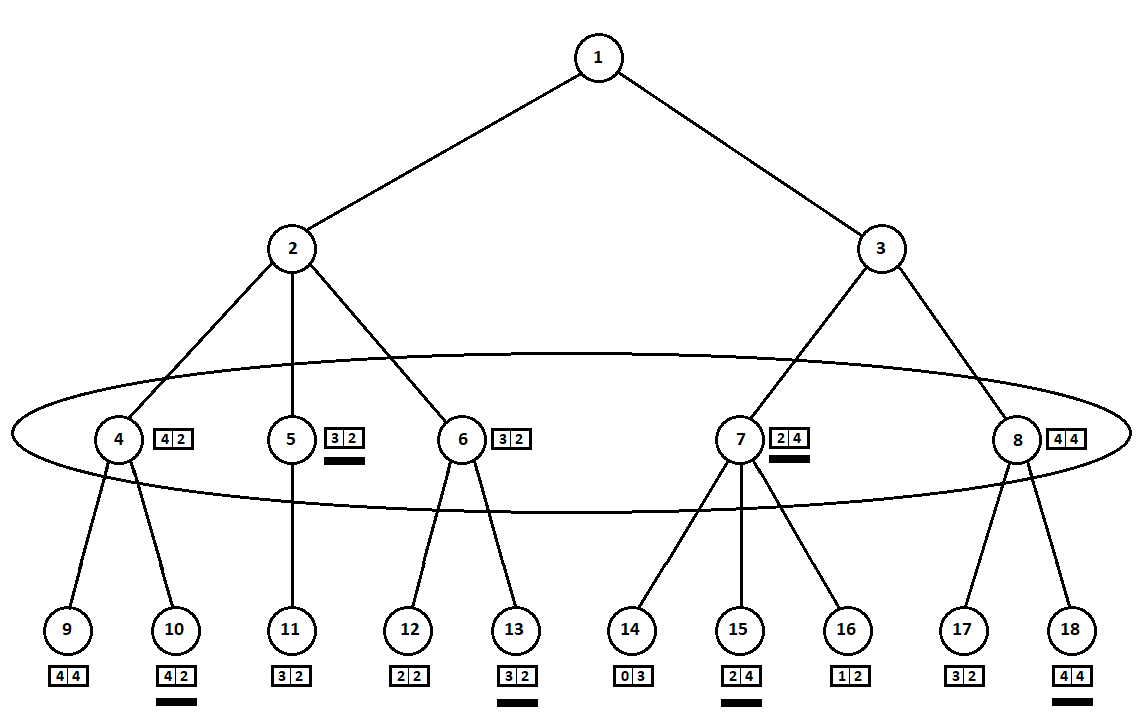
敵は明らかに、自分にとって最高の格付けを持つ位置(ベクトルの2番目の座標が最大の値を取る位置)を選択します。 これらの推定値は、グラフで再び下線が引かれています。
最後に、非常に最初の動きに戻ります。 コンピューターが選択し、彼はベクトルの最初の座標が最大の動きを好む:
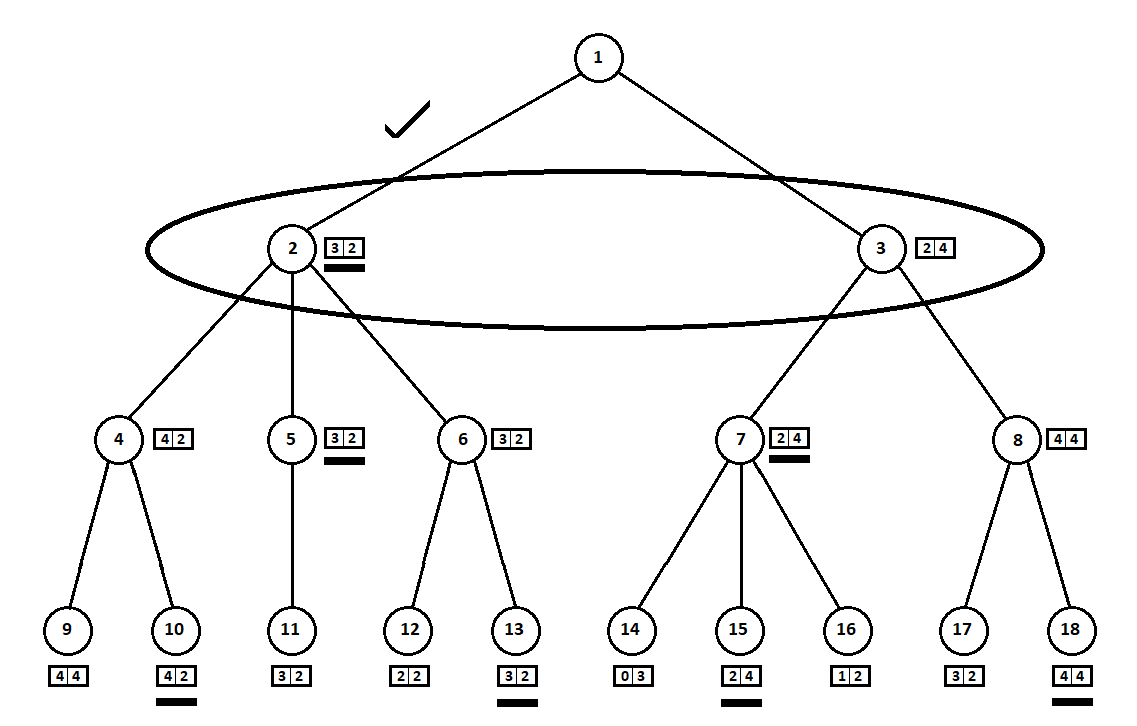
したがって、問題は解決されました-準最適な動きが見つかりました。 ツリー上のリーフ位置の100%のヒューリスティックスコアが将来の勝者を示しているとします。 それから、私たちのアルゴリズムは間違いなく可能な限り最高の動きを選択します。
ただし、ヒューリスティックスコアは、ゲームの最終位置が評価された場合にのみ100%正確です。1人(または複数の)プレイヤーが終了し、勝者が決定されます。 したがって、Nの動きを先読みする機会があれば、同じ強さのライバルを獲得するのに必要な数だけ、最適な動きを選択できます。
しかし、2人のプレーヤーの典型的なゲームは、平均で約30-40動きます(3人のプレーヤー-約60動きなど)。 各ポジションから、プレイヤーは通常約8の動きをすることができます。 したがって、30の動きの可能な位置の完全なツリーは、およそ
= 1237940039285380274899124224ピーク!
実際には、PCで〜100,000ポジションのツリーを構築および「解析」するには約300ミリ秒かかります。 コンピューターの応答を1秒以下にしたい場合、7〜8レベル(移動)でツリーの深さの制限が与えられます。
ソフトウェア実装の機能
位置のツリーを構築し、最適な動きを見つけるには、明らかに再帰的なメソッドが必要です。 メソッドの入力には、現在の位置(覚えているように、プレーヤーが移動している)と現在のツリーレベル(移動番号)があります。 アルゴリズムの設定で許可されている最大レベルに達すると、関数は各プレーヤーの「視点」からのヒューリスティックな位置推定ベクトルを返します。
重要な追加 :現在のプレイヤーが終了したら、ツリーの下の下降も停止しなければなりません。 それ以外の場合(他のプレイヤーの位置に対して最適な位置を選択するアルゴリズムが選択されている場合)、プログラムはフィニッシュで長時間「踏み鳴らし」、相手を「あざける」ことができます。 さらに、この方法で、エンドゲームのツリーのサイズをわずかに小さくします。
まだ最終的な再帰レベルに達していない場合は、可能な移動を選択し、各移動の新しい位置を作成して、現在のメソッドの再帰呼び出しに渡します。
重要な追加 :現在のプレイヤーが終了したら、ツリーの下の下降も停止しなければなりません。 それ以外の場合(他のプレイヤーの位置に対して最適な位置を選択するアルゴリズムが選択されている場合)、プログラムはフィニッシュで長時間「踏み鳴らし」、相手を「あざける」ことができます。 さらに、この方法で、エンドゲームのツリーのサイズをわずかに小さくします。
まだ最終的な再帰レベルに達していない場合は、可能な移動を選択し、各移動の新しい位置を作成して、現在のメソッドの再帰呼び出しに渡します。
ミニマックスはなぜですか?
プレイヤーの元の解釈では常に2です。 プログラムは、最初のプレーヤーの位置からのみスコアを計算します。 したがって、「最適な」ポジションを選択する場合、インデックス0のプレーヤーは最大評価のポジションを探し、インデックス1のプレーヤーは最小レーティングを探します。
私たちの場合、格付けはベクトルである必要があります。これにより、N人のプレイヤーのそれぞれが「視点」から評価できるようになります。
私たちの場合、格付けはベクトルである必要があります。これにより、N人のプレイヤーのそれぞれが「視点」から評価できるようになります。
AIのチューニング
コンピューターと対戦する私の練習は、アルゴリズムがそれほど悪くないが、それでも人間に劣ることを示しました。 私は2つの方法でAIを改善することにしました。
- 決定木の構築/走査を最適化し、
- ヒューリスティックを改善します。
ミニマックスアルゴリズムの最適化
上記の例では、位置8の検討を拒否し、ツリーの2〜3頂点を「保存」できます。
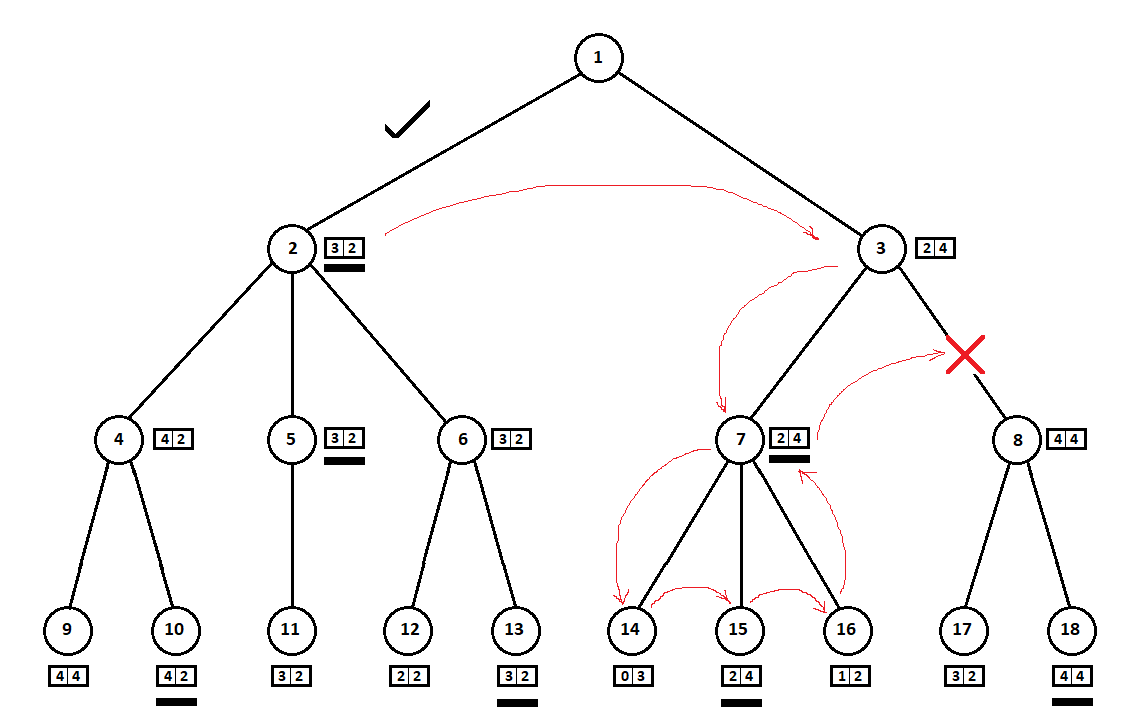
木の周りを上から下、左から右へ歩きます。 位置2から始まるサブツリーをバイパスして、移動1-> 2の最適な推定を推定しました:[3、2]。 位置7にルートを持つサブツリーをバイパスして、現在の(移動3-> 7に最適な)評価を決定しました:[2、4]。 コンピューター(最初のプレーヤー)の観点からは、スコア[2、4]はスコア[3、2]よりも悪いです。 また、コンピューターの対戦相手は、ポジション8のスコアに関係なく、ポジション3からの移動を選択するため、ポジション3の最終スコアは、3番目のポジションで得られたスコアよりもアプリオリに悪くなります。 したがって、位置8にルートを持つサブツリーは構築できず、評価できません。
Minimaxアルゴリズムの最適化されたバージョンは、余分なサブツリーを切り取ることができるため、アルファベータクリッピングアルゴリズムと呼ばれます 。 このアルゴリズムを実装するには、ソースコードを少し変更する必要があります。
ソフトウェア実装の機能
2つの整数パラメーターが、TurnMakerクラスのCalcEstimateメソッドに追加で渡されます。最初はint.MinValueに等しいalphaと、int.MaxValueに等しいbetaです。 さらに、考慮中の現在の移動の推定値を受信した後、フォームの擬似コードが実行されます。
e = _[0] // ( ) (e > alpha) alpha = e (e < beta) beta = e (beta <= alpha)
ソフトウェア実装の重要な機能
定義上、アルファ-ベータクリッピング法は、「クリーンな」ミニマックスアルゴリズムと同じソリューションにつながります。 意思決定のロジックが変更されたかどうかを確認するために(または結果が移動である)、ロボットが2人の対戦相手ごとに8回の移動(合計16回の移動)を行い、結果の一連の移動を保存するユニットテストを作成しました。クリッピングオプションを無効にしました。
次に、同じテストで、クリッピングオプションを有効にして手順を繰り返しました。 その後、一連の動きが比較されました。 動きの不一致は、アルファ-ベータクリッピングアルゴリズムの実装にエラーがあることを示します(テストに失敗しました)。
次に、同じテストで、クリッピングオプションを有効にして手順を繰り返しました。 その後、一連の動きが比較されました。 動きの不一致は、アルファ-ベータクリッピングアルゴリズムの実装にエラーがあることを示します(テストに失敗しました)。
マイナーアルファベータクリッピングの最適化
AI設定でクリッピングオプションを有効にすると、位置ツリーの頂点の数が平均3倍減少しました。 この結果は多少改善される可能性があります。
上記の例では:

位置3の頂点を持つサブツリーの前に位置2の頂点を持つサブツリーを調べたので、「一致」しました。シーケンスが異なる場合、「最悪」のサブツリーから始めて、次の位置を検討しても意味がないという結論に達しませんでした。
原則として、ツリーでのクリッピングはより「経済的」であることが判明し、同じレベル(つまり、iポジションからのすべての可能な移動)の子孫頂点は、現在の(深く見ないで)位置推定によって既にソートされています。 言い換えると、(ヒューリスティックな観点から)最高の動きはより良い最終グレードを獲得する可能性が高いと想定しています。 したがって、「最悪の」サブツリーの前に「最良の」サブツリーが考慮されるように、何らかの確率でツリーをソートします。これにより、より多くのオプションを切り捨てることができます。
現在の位置の評価は、費用のかかる手順です。 以前に終端位置(葉)のみを評価するのに十分だった場合、ツリーのすべての頂点に対して評価が行われます。 ただし、テストで示されたように、行われた評価の総数は、考えられる動きの最初の並べ替えを行わなかったバリアントよりもまだわずかに少なかった。
ソフトウェア実装の機能
アルファ-ベータクリッピングアルゴリズムは、元のミニマックスアルゴリズムと同じ動きを返します。 これは、私たちが書いた単体テストをチェックし、2つの動きのシーケンスを比較します(クリッピングありとなしのアルゴリズムの場合)。 ソートを使用したアルファベータクリッピングは、一般的な場合、準最適な動きとして異なる動きを示す場合があります。
変更されたアルゴリズムの正しい動作をテストするには、新しいテストが必要です。 変更にもかかわらず、並べ替えのあるアルゴリズムは、元のMinimaxアルゴリズムとして並べ替えのないアルゴリズムとまったく同じ最終推定ベクトル (図の例では[3、2])を生成する必要があります。
テストでは、一連のテスト位置を作成し、「最適な」移動に従ってそれぞれから選択し、ソートオプションをオンまたはオフにしました。 次に、2つの方法で得られた評価ベクトルを比較しました。
変更されたアルゴリズムの正しい動作をテストするには、新しいテストが必要です。 変更にもかかわらず、並べ替えのあるアルゴリズムは、元のMinimaxアルゴリズムとして並べ替えのないアルゴリズムとまったく同じ最終推定ベクトル (図の例では[3、2])を生成する必要があります。
テストでは、一連のテスト位置を作成し、「最適な」移動に従ってそれぞれから選択し、ソートオプションをオンまたはオフにしました。 次に、2つの方法で得られた評価ベクトルを比較しました。
さらに、ツリーの現在の最上部にある可能性のある各移動の位置はヒューリスティック評価によって並べ替えられるため、最悪のオプションの一部をすぐに破棄するように考えています。 たとえば、チェスプレーヤーは、ポーンヒットの代わりにルークを使用するムーブを検討できます。 ただし、状況を3、4 ...前方に深く「展開」することにより、例えば、対戦相手が女王の司教を攻撃している場合、彼はすぐに選択肢に気付くでしょう。
AI設定では、「最悪のオプションのクリッピング」ベクトルを設定します。 たとえば、形式[0、0、8、8、4]のベクトルは、次のことを意味します。
- 1 [0]ステップと2 [0]ステップ進むと、プログラムは考えられるすべての動きを考慮します。 0 ,
- [8] [8] , 8 “” , , ,
- 5つ以上のステップ[4]を見ると、プログラムは4つ以下の「ベスト」ムーブを評価します。
アルファベータクリッピングアルゴリズムのソートがオンになり、クリッピング設定で同様のベクトルが使用されると、プログラムは約300ミリ秒を費やし、「より深く」8歩進む準最適な動きを選択し始めました。
ヒューリスティック最適化
ツリーの頂点の位置がかなりの量で繰り返され、準最適な動きを求めて「深く」先を見据えているにもかかわらず、AIにはいくつかの弱点がありました。それらの1つを「ウサギのわな」と定義しました。
うさぎトラップ
. ( 8 — 10 15), . “” ( !):
. 例を挙げます。
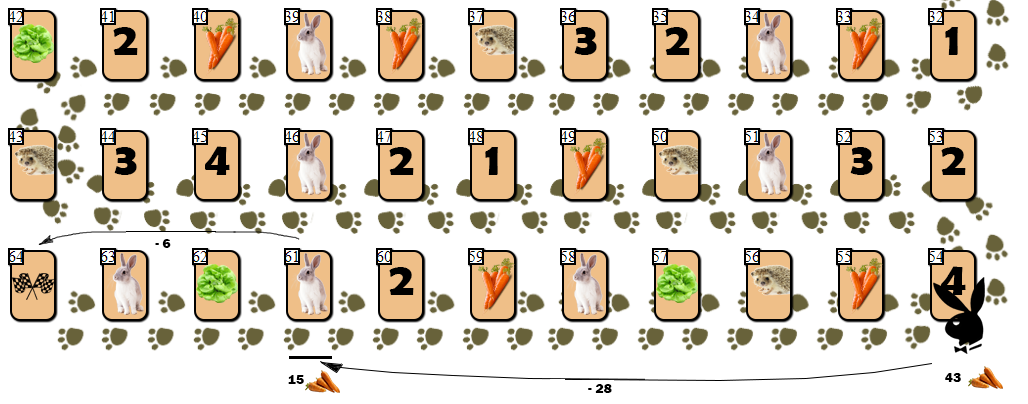
54 (43), — 10 55 . AI, , (61), 28 . , 6 9 ( 10 ).
, ( ), , 4 — 6 . , , , AI ?
, , . AI . , , . “ ” :
65 — “” , , . , , , () .
- 7,
- , , . , , , .
. 例を挙げます。

54 (43), — 10 55 . AI, , (61), 28 . , 6 9 ( 10 ).
, ( ), , 4 — 6 . , , , AI ?
, , . AI . , , . “ ” :
65 — “” , , . , , , () .
補正係数
前に、現在の位置の発見的推定のための公式を与える
E = Ks * S + Kc * C + Kp * P、
私は言及したが、補正因子については説明しなかった。
実際には、式自体と関数のセットの両方が、いわゆる 「常識。」少なくとも、推定値が可能な限り適切になるように、このような係数Ks、Kc、Kpを選択します。評価の「妥当性」を評価する方法は?見積りは無次元の量であり、別の見積りとのみ比較できます。補正係数を改善する唯一の方法を思いつくことができました。次の形式のデータを含むCSVファイルに保存されたいくつかの「研究」をプログラムに入れました
45;26;2;f;29;19;0;f;2 ...
この行は、文字通り次を意味します。
- 最初のプレイヤーは45番で、26枚のニンジンと2枚のサラダカードを手に持っています。プレイヤーは動きを見逃しません(f = false)。移動する権利は常に最初のプレイヤーです。
- セル29の2番目のプレイヤーは、19枚のニンジンとサラダカードを使用せず、動きを見逃しません。
- 2番目の数字は、調査を「決定」することを意味し、2番目のプレーヤーが勝ちの状況にあると仮定しました。
プログラムに20個のスケッチを入れた後、ゲームWebクライアントにそれらを「ダウンロード」し、スケッチされた各スケッチをソートしました。スケッチを分析して、「勝者」を決めるまで、プレーヤーごとに交互に移動しました。評価が終了したら、特別なチームでサーバーに送信しました。
20の練習曲を評価した後(もちろん、さらに多くの練習曲を分析する価値があります)、プログラムで各練習曲を評価しました。評価中、0.5から2までの各補正係数の値、0.1の増分-合計 =係数のトリプルの4096バリアント。最初のプレーヤーのスコアが2番目のプレーヤーのスコアより高いことが判明し、同様の指示がエチュードレコードの行に保存された場合(行の最後の値は1)、「ヒット」がカウントされました。ミラー状況の場合も同様です。それ以外の場合、スリップがカウントされました。その結果、「ヒット」の割合が最大であるトリプル(20のうち16)を選択しました。 4096個のベクターのうち約250個が出てきましたが、その中から「最良」を選択し、「目で」もう一度選択して、AI設定にインストールしました。
まとめ
その結果、動作するプログラムを手に入れました。これは原則として、コンピューターに対して1対1のバージョンで私を打ち負かします。プログラムの現在のバージョンの勝利と敗北に関する重大な統計はまだ蓄積されていません。おそらく、その後の簡単なAIチューニングにより、私の勝利は不可能になります。または、うさぎ細胞因子がまだ残っているため、ほとんど不可能です。
たとえば、レーティング(絶対最大値または他のプレーヤーに対する最大値)を選択するロジックでは、間違いなく中間オプションを試してみます。少なくとも、i番目のプレーヤーのスコアの絶対値が等しい場合、スコアの相対値が高い位置(高貴なレスリーと裏切り者のフェイスのハイブリッド)につながる動きを選択するのが合理的です。
このプログラムは、3人のプレイヤーがいるバージョンで完全に機能します。ただし、3人のプレーヤーでプレイする場合のAIの動きの「品質」は、2人のプレーヤーでプレイする場合よりも低いという疑いがあります。しかし、最後のテストの過程でコンピューターに負けました-おそらく過失によって、私の手の中のニンジンの量を何気なく評価し、過剰な「燃料」でフィニッシュラインに到達しました。
これまでのところ、AIのさらなる発展は、「テスター」、つまりコンピューターの「天才」の生きた敵である人の不足によって妨げられています。私自身、うさぎとハリネズミを吐き気がするほど十分に演奏し、現在の段階で強制的に中断させました。
→ ソースを含むリポジトリへのリンク