マージは、この原則に従って作業をソートします。

1. 順序付けられた部分配列が検索されます（オプションとして-形成されます）。
2. 順序付けられた部分配列は、共通の順序付けられた部分配列に連結されます。

それ自体では、配列内の順序付けられたサブ配列はあまり価値がありません。 しかし、配列内で2つの順序付けられたサブ配列が見つかった場合、これはまったく別の問題です。 実際には、それらを非常に迅速かつ最小限のコストでマージできます-順序付けられたサブアレイのペアから一般的な順序付けられたサブアレイを形成するため







ご覧のとおり、2つの配列を1つに結合するのは簡単ではありませんが、非常に簡単です。 両方の配列を左から右に同時に移動し、両方の配列の次の要素のペアを比較する必要があります。 小さい要素は共通のボイラーに送られます。 要素が配列の1つで終わると、他の配列の残りの要素が単純に順番にメインリストに転送されます。



これは、このクラスのアルゴリズムの塩です。 最初に、ランダム配列は多くの小さな順序付きサブ配列に分割できます。 ペアワイズマージでは、順序付けられたサブアレイの数が減少し、それぞれの長さが増加します。 最後のステップで、配列は、単一の順序付けられた構造にマージされる2つの順序付けられたサブ配列のみで構成されます。




このコンセプトの作者はジョン・フォン・ノイマンです。 彼は、核爆弾の開発において膨大な量の統計データの効果的な計算を提供するタスクに直面したため、マンハッタンのプロジェクトに取り組んでいる間にソートを思いついたという論争の的となる主張が時々あります。 このバージョンの信頼性を評価することは困難です。合併による分類に関する彼の最初の研究は1948年にさかのぼり、爆弾の作成は3年前に完了したためです。 ただし、どのようなアトミックソートがありますか、見てみましょう。

ナチュラルノイマンフュージョン

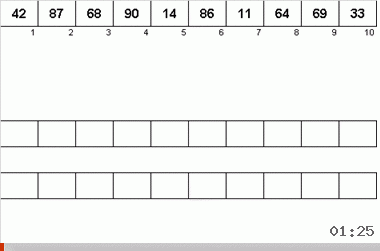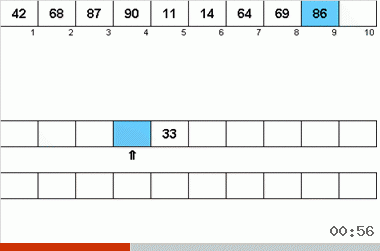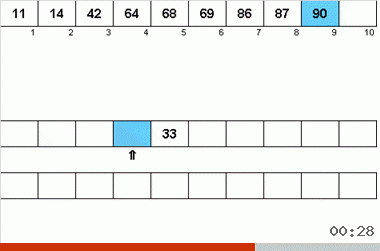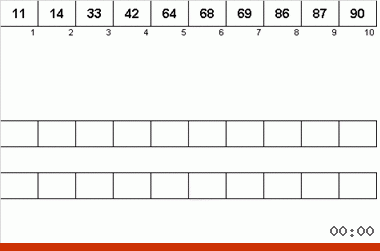
ネイマンアルゴリズムは、40年代のコンピューターの設計機能の影響を受けました。 このように見えた：

1. 合計で3つの磁気テープが使用されます。メインの磁気テープには、未分類のデータと2つの補助データが記録されます。
2. データはメインテープから順次読み取られます。
3. 順次読み取られるデータは順序付けられたサブアレイですが、補助テープのいずれかにコピーされます。
4. 次のソートされたサブアレイが完了すると（つまり、前のサブアレイよりも小さい要素がメインテープで見つかると）、ポインタが補助テープ（サブアレイの終わり）に置かれ、別の補助テープへの切り替えが発生します。
5. ポイント2〜4が再び繰り返され、データのみが別の補助テープに転送されます。 次の順序のサブアレイの最後で、メインテープは1つの補助テープに交互に切り替わり、次に別のテープに切り替わります。
6. プライマリテープからすべてのデータが読み取られると、補助テープの処理が行われます。
7. 両方の補助テープは順番にデータを読み取ります。
8. この場合、2本のテープの次のデータが互いに比較されます。 比較結果に基づいて、ペアの最小要素がメインテープに記録されます。
9. 補助テープ上の配列の境界はポインターでマークされているため、読み取りと比較はソートされたサブ配列の制限内でのみ行われます。
10. 補助テープの1つで次のサブアレイの要素が終わった場合、残りのテープからサブアレイの残りがメインテープに単純に転送されます。
11. メインテープ上のデータが完全に順序付けられたアレイになるまで、プロセス全体を繰り返します。

ノイマンソートは適応アルゴリズムです：配列のソートされた部分を修正するだけでなく、まずそれらを増加させようとするため、細長い順序付きサブアレイに基づいてさらに長い順序付きサブアレイを形成します。 したがって、 適応マージソートとも呼ばれます。



このアルゴリズムの複雑さは控えめです-O（ n ² ）、それにもかかわらず、チューブコンピューティングの先駆者にとって、これはブレークスルーでした。



この最初のマージソートの例では、このクラスのアルゴリズムの欠点はすでに明らかになっています-追加メモリのコスト。 この点で、ほとんどすべてのマージソートでO（ n ）が追加で必要になりますが、エレガントな例外はまれです。

ボウズ・ネルソンの直接合併

厳密に言えば、Bowes-Nelsonアルゴリズムはソートではなく、ソートネットワークです。 このプロセスでは、アレイとそのすべてのサブアレイが半分に分割され、これらの半分がすべての段階で並列処理されることを妨げるものはありません。 ただし、並べ替えの形式で表すこともできます。 また、ネットワークの並べ替えのトピックも取り上げます。

1. 配列は半分に分割されます-左半分と右半分に。
2. 要素はグループに分けられます。
3. 最初の反復では、これらは2つの要素（左半分の1番目の要素+右半分の1番目の要素、左半分の2番目の要素+右半分の2番目の要素など）、2番目の反復-4つの要素（1-左半分の2番目と2番目の要素+右半分の1番目と2番目の要素、左半分の3番目と4番目の要素+右半分の3番目と4番目の要素など）、3番目に-エイトなど
4. 左半分の各グループの要素はソートされたサブアレイであり、右半分の各グループの要素もソートされたサブアレイです。
5. 前の段落のソートされたサブ配列をマージします。
6. ポイント1に戻ります。サイクルは、グループのサイズが配列のサイズより小さくなるまで続きます。

ここでは、追加のメモリが必要と思われるかもしれません。 しかし、違います！ アニメーションをより理解しやすくするために、比較対象のサブアレイの相対位置がより明確になるように、アレイの左半分と右半分を互いに配置します。 ただし、半分に厳密に分割されているため、メモリから追加のリソースを引き付けることなく、すべての比較と交換が適切に行われるアルゴリズムが可能です。 これはマージソートでは非常に珍しいことです。

def bose_nelson(data): m = 1 while m < len(data): j = 0 while j + m < len(data): bose_nelson_merge(j, m, m) j = j + m + m m = m + m return data def bose_nelson_merge(j, r, m): if j + r < len(data): if m == 1: if data[j] > data[j + r]: data[j], data[j + r] = data[j + r], data[j] else: m = m // 2 bose_nelson_merge(j, r, m) if j + r + m < len(data): bose_nelson_merge(j + m, r, m) bose_nelson_merge(j + m, r - m, m) return data
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

すべてのソートマージには、水素爆弾に似たものがあります。 最初に分割され、次に合成されます。

参照資料

マージ / マージ

シリーズ記事：

• ExcelアプリケーションAlgoLab.xlsm
• 交換ソート
• 挿入ソート
• 選択で並べ替え
• ソートのマージ
  • トップダウンとボトムアップのバランスの取れた合併
  • マルチフェーズマージソート
  • カスケードマージソート
  • 振動マージソート
  • スレッド化された非混合ソート
  • ソート比較のマージ
• 分布で並べ替え

今日の記事で言及した両方の並べ替えがAlgoLabアプリケーションで利用できるようになりました（このExcelアプリケーションを使用してアルゴリズムを学習する人は、ファイルを更新してください）。 そして、数日のうちに、マージソートに関する次の続編がリリースされると、このクラスのアルゴリズムがさらにいくつか利用できるようになります。



Bowes-Nelsonの並べ替えには制限があります-配列のサイズは2のべき乗でなければなりません。 この条件が満たされない場合、マクロは配列を適切なサイズにトリミングします。

この記事は、 3D再構築ソフトウェアを作成し、高度な測定機器を開発している EDISON Softwareの支援を受けて作成されました。