それで、「指の数学」のサイクルからの別の記事。今日は最小二乗法の議論を続けますが、今回はプログラマーの観点からです。これはシリーズの別の記事ですが、数学の知識を必要としないため、際立っています。この記事は理論の入門書として考案されたので、基本的なスキルからコンピューターの電源を入れて5行のコードを書く能力が必要です。もちろん、私はこの記事にこだわることはせず、近い将来に続編を発行します。十分な時間を見つけられたら、この資料から本を書きます。ターゲットオーディエンスはプログラマーなので、Habrは侵入するのに最適な場所です。一般に、式を書くのは好きではなく、例から学ぶのが本当に好きです。これは非常に重要だと思われます-教育委員会の波線を見るだけでなく、歯のすべてを試してください。

それでは始めましょう。私の顔をスキャンした三角形の表面があることを想像してみましょう（左の写真）。この表面をグロテスクなマスクに変えて、機能を強化するには何をする必要がありますか？

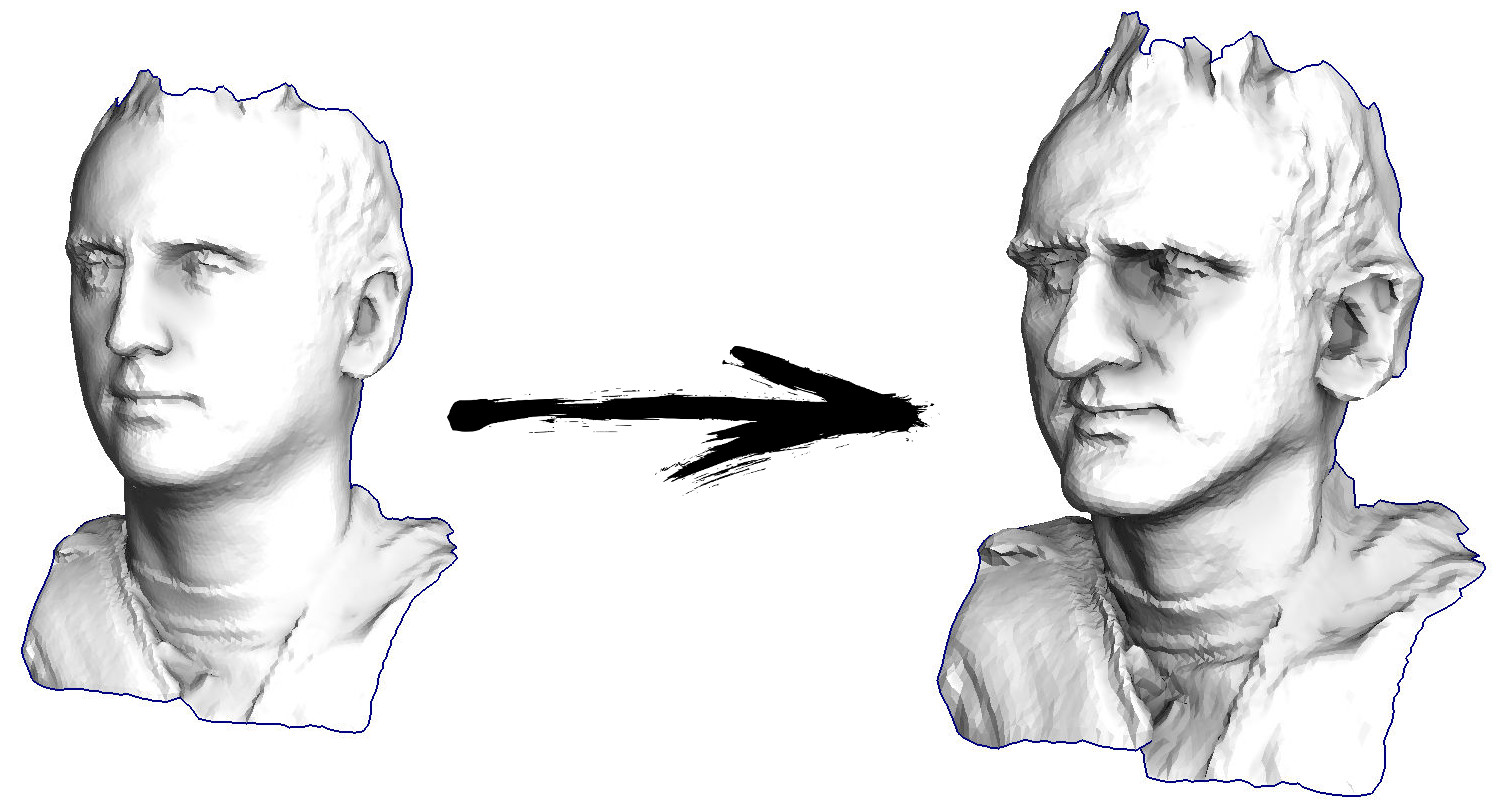
この特定のケースでは、 Simeon Demi Poissonという名前の楕円微分方程式を解きます。プログラマーの仲間、ゲームをプレイしましょう。それを決定するC ++コードに何行あると思いますか？サードパーティのライブラリを呼び出すことはできません。使用できるのは、裸のコンパイラのみです。答えは下にあります。

実際、ソルバーには20行のコードで十分です。 3Dモデルファイルのパーサーを含むすべてのものを数えると、200行以内に収まります-ただ吐き出します。

例1：データの平滑化

それがどのように機能するかについて話しましょう。遠くから始めましょう。たとえば、32要素の通常の配列fがあり、次のように初期化されているとします。

そして、次の手順を千回実行します。各セルf [i]に対して、隣接セルの平均値を書き込みます：f [i] =（f [i-1] + f [i + 1]）/ 2。より明確にするために、完全なコードを次に示します。

import matplotlib.pyplot as plt f = [0.] * 32 f[0] = f[-1] = 1. f[18] = 2. plt.plot(f, drawstyle='steps-mid') for iter in range(1000): f[0] = f[1] for i in range(1, len(f)-1): f[i] = (f[i-1]+f[i+1])/2. f[-1] = f[-2] plt.plot(f, drawstyle='steps-mid') plt.show()

各反復は配列のデータを平滑化し、1000回の反復後、すべてのセルで一定の値を取得します。以下に、最初の150回の反復のアニメーションを示します。

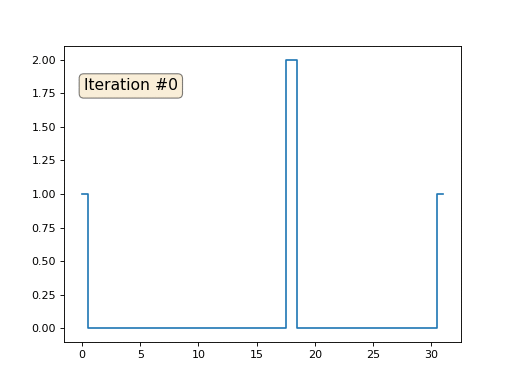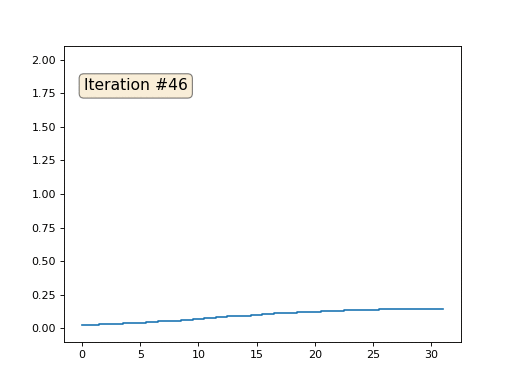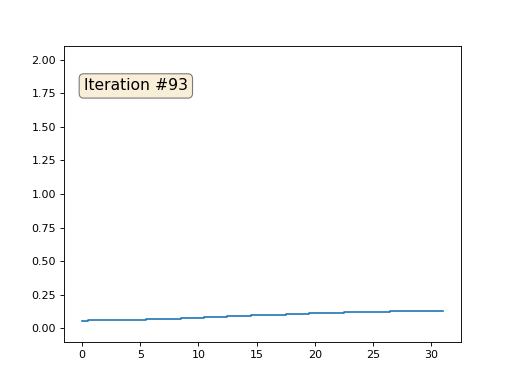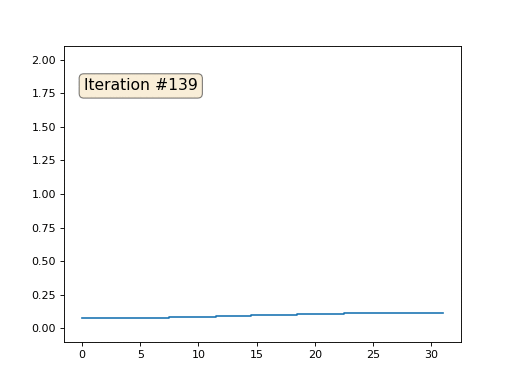
アンチエイリアシングが発生する理由が明確でない場合は、今すぐ停止し、ペンをつかんで例を描いてみてください。そうでない場合、読み上げは意味がありません。三角形の表面は、この例と本質的に同じです。各頂点について、隣接する頂点を見つけ、それらの重心を計算し、頂点をこの重心に移動することを10回繰り返します。結果は次のようになります。

もちろん、10回の繰り返しで停止しない場合、しばらくすると、前の例とまったく同じ方法で表面全体が1ポイントに圧縮され、配列全体が同じ値でいっぱいになります。

例2：機能の強化/減衰

完全なコードはgithubで入手できますが、ここでは3Dモデルの読み取りと書き込みのみを省略し、最も重要な部分を説明します。したがって、私にとっての三角形モデルは、頂点と面の2つの配列で表されます。 verts配列は3次元の点の集合であり、ポリゴンメッシュの頂点でもあります。 faces配列は三角形のセットです（三角形の数はfaces.size（）に等しくなります）。各三角形について、頂点配列からのインデックスが配列に格納されます。データ形式とそれを使用した作業については、コンピューターグラフィックスに関する講義で詳しく説明しました。 3番目の配列もあります。最初の2つ（より正確には、faces配列のみ）から数えます-vvadj。これは、各頂点（2次元配列の最初のインデックス）に隣接するインデックス（2番目のインデックス）を格納する配列です。

 std::vector<Vec3f> verts; std::vector<std::vector<int> > faces; std::vector<std::vector<int> > vvadj;

最初に行うことは、サーフェスの各頂点について、曲率ベクトルを考慮することです。説明してみましょう。現在の頂点vについて、そのすべての近傍n1〜n4を反復処理します。次に、それらの重心b =（n1 + n2 + n3 + n4）/ 4。さて、最終的な曲率ベクトルはc = vbとして計算できます。これは、2次導関数の通常の有限差分とは異なります。

コード内で直接、次のようになります。

  std::vector<Vec3f> curvature(verts.size(), Vec3f(0,0,0)); for (int i=0; i<(int)verts.size(); i++) { for (int j=0; j<(int)vvadj[i].size(); j++) { curvature[i] = curvature[i] - verts[vvadj[i][j]]; } curvature[i] = verts[i] + curvature[i] / (float)vvadj[i].size(); }

それでは、次のことを何度も行います（前の図を参照）。頂点vをvに移動します。= b + const * c。定数が1に等しい場合、頂点はどこにも移動しないことに注意してください！定数がゼロの場合、頂点は隣接する頂点の重心に置き換えられ、表面が滑らかになります。定数が1よりも大きい場合（タイトル画像はconst = 2.1を使用して作成された）、頂点は表面の曲率ベクトルの方向にシフトし、詳細を強化します。これはコードでどのように見えるかです：

  for (int it=0; it<100; it++) { for (int i=0; i<(int)verts.size(); i++) { Vec3f bary(0,0,0); for (int j=0; j<(int)vvadj[i].size(); j++) { bary = bary + verts[vvadj[i][j]]; } bary = bary / (float)vvadj[i].size(); verts[i] = bary + curvature[i]*2.1; // play with the coeff here } }

ちなみに、それが1未満の場合、詳細は逆に弱くなります（const = 0.5）が、これは単純なスムージングと同等ではなく、「画像のコントラスト」は残ります：

私のコードは、サードパーティのプログラムでレンダリングしたWavefront .obj形式の3Dモデルファイルを生成することに注意してください。結果のモデルは、たとえばオンラインビューアーで確認できます。モデルを生成するのではなく、メソッドの描画に興味がある場合は、コンピューターグラフィックスに関する私のコースを読んでください。

例3：制約の追加

最初の例に戻って、まったく同じことを行いますが、0、18、31の数字の下にある配列の要素は書き換えません。

 import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2. plt.plot(x, drawstyle='steps-mid') plt.show()

配列の残りの「空き」要素をゼロで初期化し、それらを繰り返し、隣接する要素の平均値で置き換えます。これは、最初の150回の反復で配列の進化がどのように見えるかです。

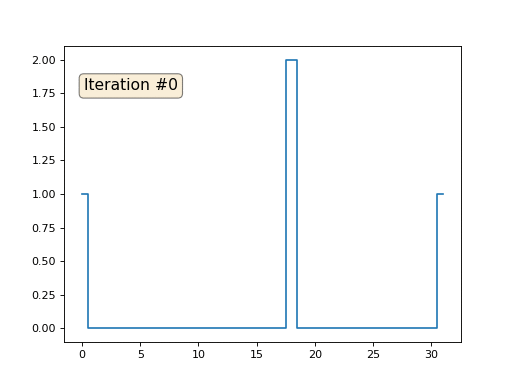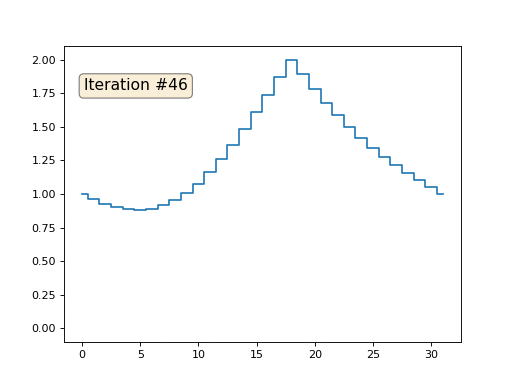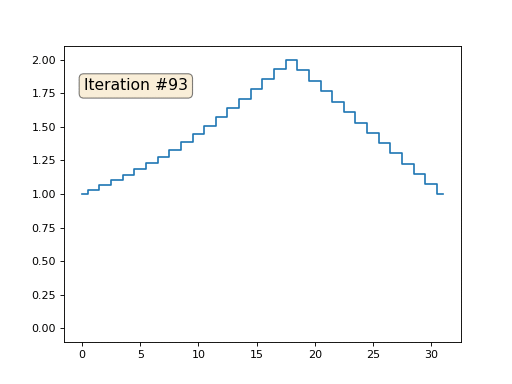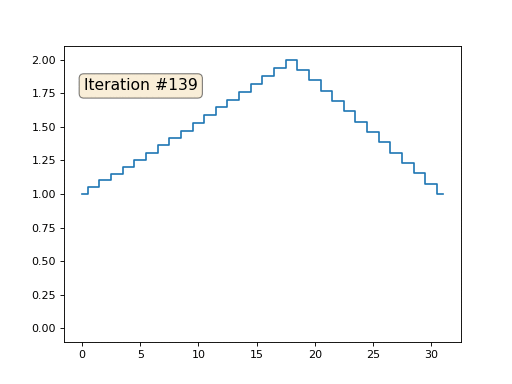
今回は、解が配列を満たす一定の要素ではなく、2つの線形ランプに収束することは明らかです。ちなみに、それは誰にとっても本当に明らかですか？そうでない場合は、このコードを試して、何が起こっているかを完全に理解できるように、非常に短いコードの例を具体的に示します。

叙情的余談：線形方程式系の数値解。

通常の線形連立方程式を考えてみましょう。

これは書き直すことができ、片側の各方程式に等号x_iを残します。

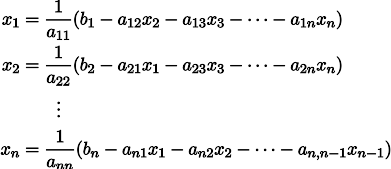
任意のベクトルを与えてみましょう

連立方程式の解を近似する（たとえば、ゼロ）。

次に、それをシステムの右側に貼り付けると、更新された解近似ベクトルを取得できます

。

明確にするために、x0から次のようにx1を取得します。

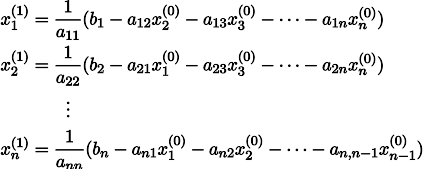
プロセスをk回繰り返すと、解はベクトルで近似されます

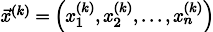
念のため、再帰式を書きます。

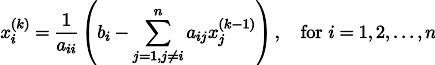
システムの係数に関するいくつかの仮定（たとえば、対角要素を分割するため、対角要素がゼロであってはならないことは明らかです）で、この手順は真の解に収束します。この体操は、文献ではヤコビ法として知られています。もちろん、線形方程式系を数値的に解く他の方法や、もっと強力なもの、たとえば共役勾配法がありますが、おそらく、ヤコビ法は最も簡単な方法の1つです。

再び例3、ただし一方で

次に、例3のメインループを詳しく見てみましょう。

 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2.

私はいくつかの初期ベクトルxから始め、それを数千回更新しましたが、更新手順はヤコビ法に疑わしく似ています！この連立方程式を明示的に記述しましょう。

少し時間をかけて、Pythonコードの各反復が、この方程式系のJacobiメソッドの厳密に1つの更新であることを確認してください。値x [0]、x [18]、およびx [31]はそれぞれ固定されており、変数のセットには含まれていないため、右側に転送されます。

合計すると、システム内のすべての方程式は-x [i-1] + 2 x [i]-x [i + 1] = 0のようになります。この式は、2次導関数の通常の有限差分にすぎません。つまり、我々の方程式系は、二次導関数がどこでもゼロに等しくなければならないことを単純に規定しています（ポイントx [18]を除く）。覚えておいて、反復が線形ランプに収束することは明らかだと言ったのですか？そのため、2次導関数の線形導関数はゼロです。

ラプラス方程式のディリクレ問題を解いたことをご存知ですか？

ところで、注意深い読者は、厳密に言えば、私のコードでは、線形方程式系はヤコビ法ではなく、ヤコビ法の一種の最適化であるガウス・ザイデル法によって解かれていることに気付くはずです。

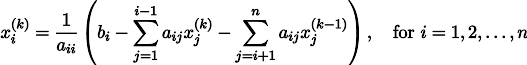
例4：ポアソン方程式

3番目の例を少し変更してみましょう。各セルは、隣接するセルの質量の中心だけでなく、質量の中心といくつかの（任意の）定数に配置されます。

 import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1] +11./32**2 )/2. plt.plot(x, drawstyle='steps-mid') plt.show()

前の例では、重心に配置することがラプラス演算子（この場合は2次導関数）の離散化であることがわかりました。つまり、現在、信号に一定の2次導関数が必要であるという方程式系を解いています。二次導関数は表面の曲率です。したがって、区分的二次関数がシステムの解決策になるはずです。 32個のサンプルのサンプリングを確認しましょう。

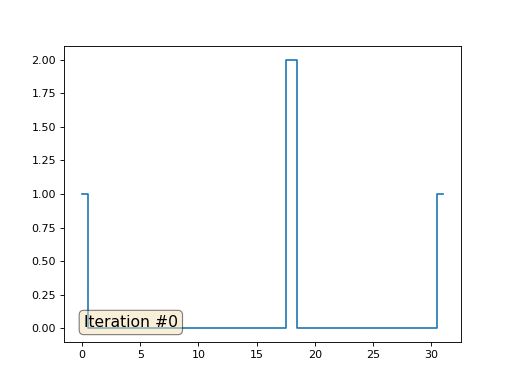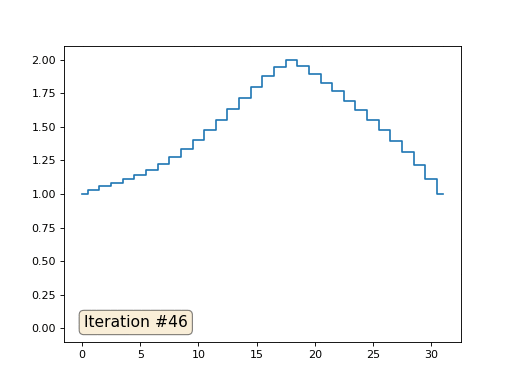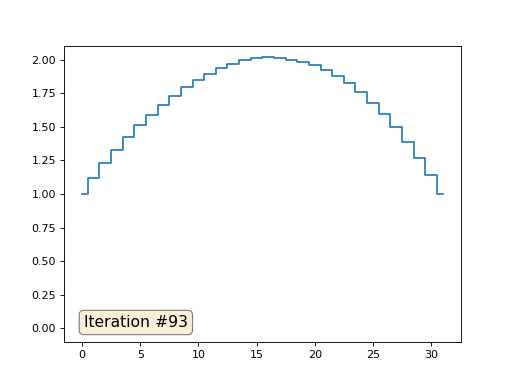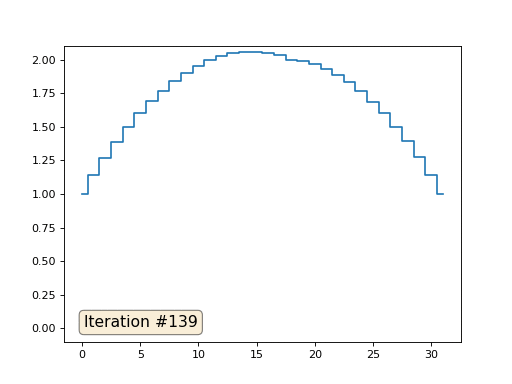
配列の長さが32要素の場合、システムは数百回の反復でソリューションに収束します。しかし、128個の要素の配列を試すとどうなりますか？ここではすべてが悲しいです。繰り返しの数はすでに数千単位で計算されている必要があります。

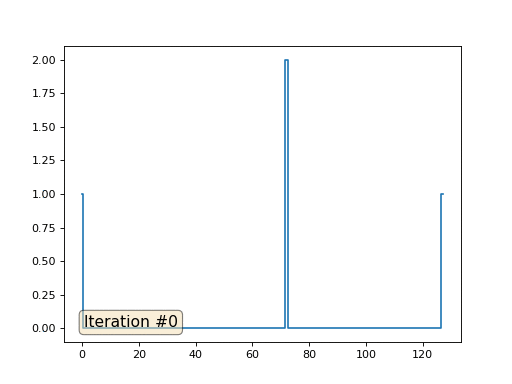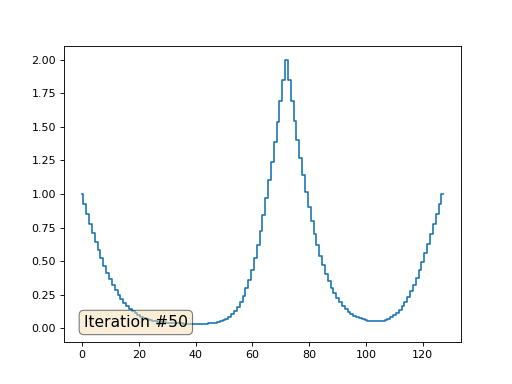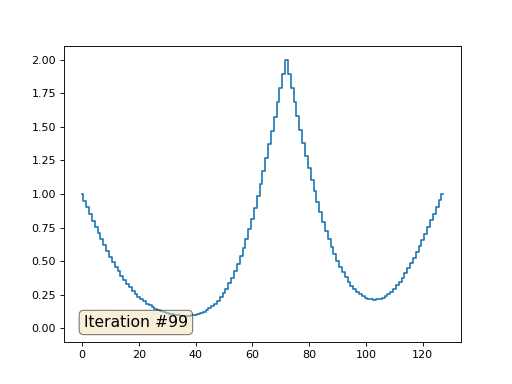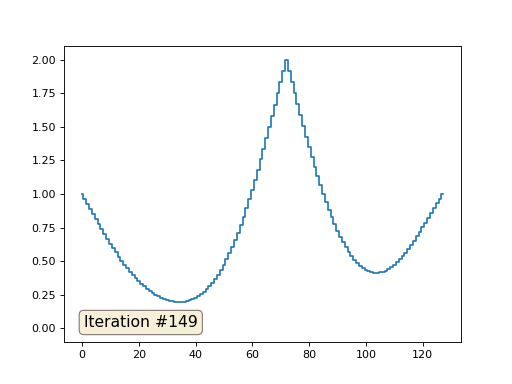
Gauss-Seidel法はプログラミングが非常に簡単ですが、大規模な方程式系には適用できません。マルチグリッドメソッドなどを使用して、高速化を試みることができます。言い換えれば、これは面倒に聞こえるかもしれませんが、アイデアは非常に原始的です：1000要素の解像度のソリューションが必要な場合は、最初に10要素で解決し、大まかな近似を取得し、次に解像度を2倍にして、もう一度解決するなど、到達するまで望ましい結果。実際には、次のようになります。

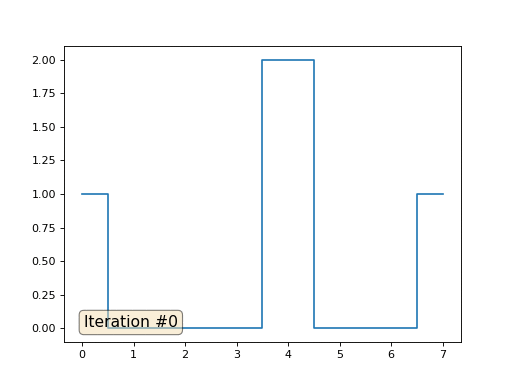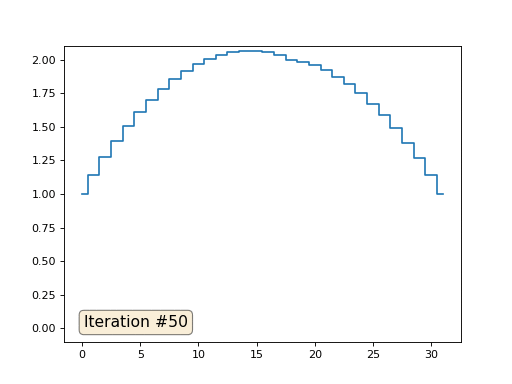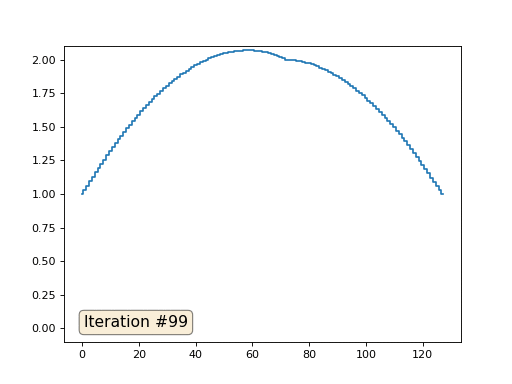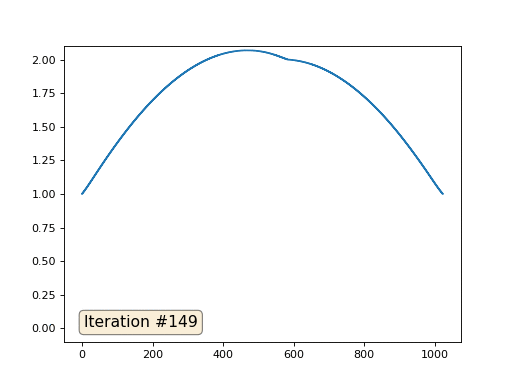
そして、あなたは誇示することはできず、方程式系の実際のソルバーを使用します。マトリックスAと列bを作成し、マトリックス方程式Ax = bを解くことにより、同じ例を解きます。

 import numpy as np import matplotlib.pyplot as plt n=1000 x = [0.] * n x[0] = x[-1] = 1. m = n*57//100 x[m] = 2. A = np.matrix(np.zeros((n, n))) for i in range(1,n-2): A[i, i-1] = -1. A[i, i] = 2. A[i, i+1] = -1. A = A[1:-2,1:-2] A[m-2,m-1] = 0 A[m-1,m-2] = 0 b = np.matrix(np.zeros((n-3, 1))) b[0,0] = x[0] b[m-2,0] = x[m] b[m-1,0] = x[m] b[-1,0] = x[-1] for i in range(n-3): b[i,0] += 11./n**2 x2 = ((np.linalg.inv(A)*b).transpose().tolist()[0]) x2.insert(0, x[0]) x2.insert(m, x[m]) x2.append(x[-1]) plt.plot(x2, drawstyle='steps-mid') plt.show()

そして、このプログラムの結果は次のとおりです。ソリューションが即座に判明したことに注意してください。

したがって、実際には、関数は区分的に2次関数です（2次導関数は定数です）。最初の例では、2番目の2次導関数をゼロに設定し、3番目は非ゼロに設定していますが、どこでも同じです。そして、2番目の例には何がありましたか？表面の曲率を指定することにより、離散ポアソン方程式を解きました。何が起こったのかを思い出させてください。入射面の曲率を計算しました。出力での表面の曲率を入力での表面の曲率と等しく設定することでポアソン問題を解決する場合（const = 1）、何も変わりません。顔の特徴の強化は、単純に曲率を増加させるときに発生します（const = 2.1）。 const <1の場合、結果のサーフェスの曲率は減少します。

更新：宿題としての別のおもちゃ

SquareRootOfZeroによって提案されたアイデアを開発し、このコードで遊んでください：

非表示のテキスト

 import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig, ax = plt.subplots() x = [282, 282, 277, 274, 266, 259, 258, 249, 248, 242, 240, 238, 240, 239, 242, 242, 244, 244, 247, 247, 249, 249, 250, 251, 253, 252, 254, 253, 254, 254, 257, 258, 258, 257, 256, 253, 253, 251, 250, 250, 249, 247, 245, 242, 241, 237, 235, 232, 228, 225, 225, 224, 222, 218, 215, 211, 208, 203, 199, 193, 185, 181, 173, 163, 147, 144, 142, 134, 131, 127, 121, 113, 109, 106, 104, 99, 95, 92, 90, 87, 82, 78, 77, 76, 73, 72, 71, 65, 62, 61, 60, 57, 56, 55, 54, 53, 52, 51, 45, 42, 40, 40, 38, 40, 38, 40, 40, 43, 45, 45, 45, 43, 42, 39, 36, 35, 22, 20, 19, 19, 20, 21, 22, 27, 26, 25, 21, 19, 19, 20, 20, 22, 22, 25, 24, 26, 28, 28, 27, 25, 25, 20, 20, 19, 19, 21, 22, 23, 25, 25, 28, 29, 33, 34, 39, 40, 42, 43, 49, 50, 55, 59, 67, 72, 80, 83, 86, 88, 89, 92, 92, 92, 89, 89, 87, 84, 81, 78, 76, 73, 72, 71, 70, 67, 67] y = [0, 76, 81, 83, 87, 93, 94, 103, 106, 112, 117, 124, 126, 127, 130, 133, 135, 137, 140, 142, 143, 145, 146, 153, 156, 159, 160, 165, 167, 169, 176, 182, 194, 199, 203, 210, 215, 217, 222, 226, 229, 236, 240, 243, 246, 250, 254, 261, 266, 271, 273, 275, 277, 280, 285, 287, 289, 292, 294, 297, 300, 301, 302, 303, 301, 301, 302, 301, 303, 302, 300, 300, 299, 298, 296, 294, 293, 293, 291, 288, 287, 284, 282, 282, 280, 279, 277, 273, 268, 267, 265, 262, 260, 257, 253, 245, 240, 238, 228, 215, 214, 211, 209, 204, 203, 202, 200, 197, 193, 191, 189, 186, 185, 184, 179, 176, 163, 158, 154, 152, 150, 147, 145, 142, 140, 139, 136, 133, 128, 127, 124, 123, 121, 117, 111, 106, 105, 101, 94, 92, 90, 85, 82, 81, 62, 55, 53, 51, 50, 48, 48, 47, 47, 48, 48, 49, 49, 51, 51, 53, 54, 54, 58, 59, 58, 56, 56, 55, 54, 50, 48, 46, 44, 41, 36, 31, 21, 16, 13, 11, 7, 5, 4, 2, 0] n = len(x) cx = x[:] cy = y[:] for i in range(0,n): bx = (x[(i-1+n)%n] + x[(i+1)%n] )/2. by = (y[(i-1+n)%n] + y[(i+1)%n] )/2. cx[i] = cx[i] - bx cy[i] = cy[i] - by lines = [ax.plot(x, y)[0], ax.text(0.05, 0.05, "Iteration #0", transform=ax.transAxes, fontsize=14,bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5)), ax.plot(x, y)[0] ] def animate(iteration): global x, y print(iteration) for i in range(0,n): x[i] = (x[(i-1+n)%n]+x[(i+1)%n])/2. + 0.*cx[i] # play with the coeff here, 0. by default y[i] = (y[(i-1+n)%n]+y[(i+1)%n])/2. + 0.*cy[i] lines[0].set_data(x, y) # update the data. lines[1].set_text("Iteration #" + str(iteration)) plt.draw() ax.relim() ax.autoscale_view(False,True,True) return lines ani = animation.FuncAnimation(fig, animate, frames=np.arange(0, 100), interval=1, blit=False, save_count=50) #ani.save('line.gif', dpi=80, writer='imagemagick') plt.show()

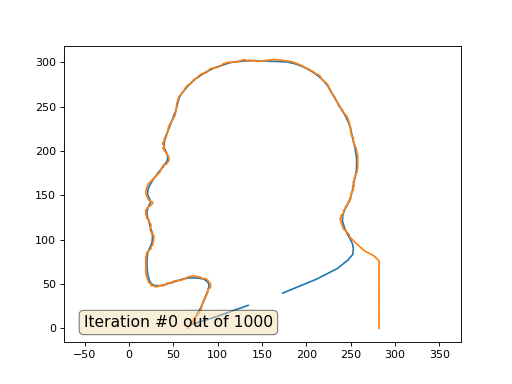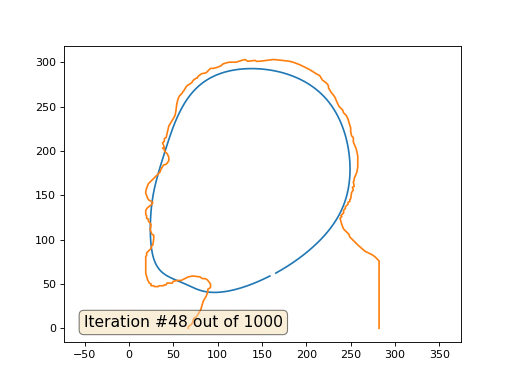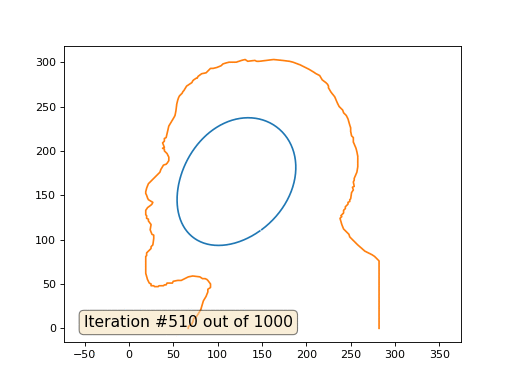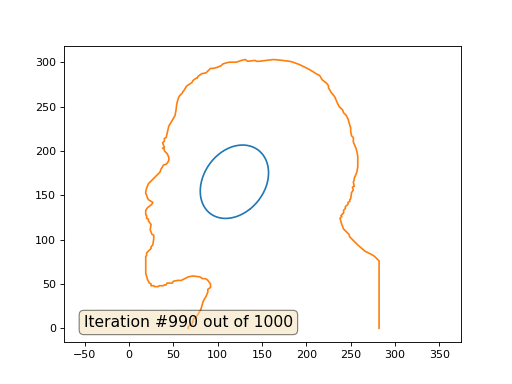
これがデフォルトの結果です。赤のレーニンが初期データ、青の曲線がそれらの進化、無限大で結果が点に収束します。

そして、これは係数2の結果です：

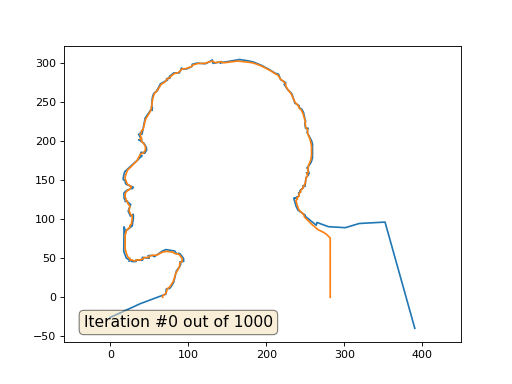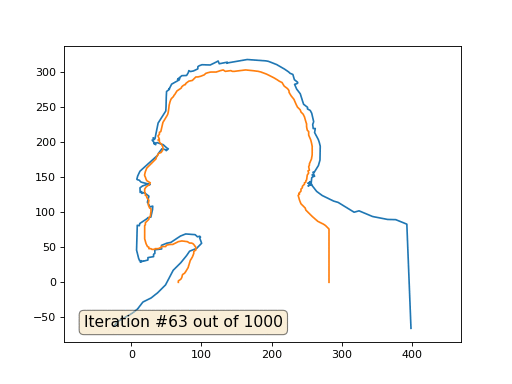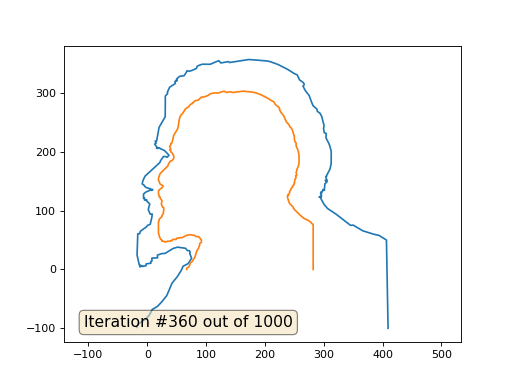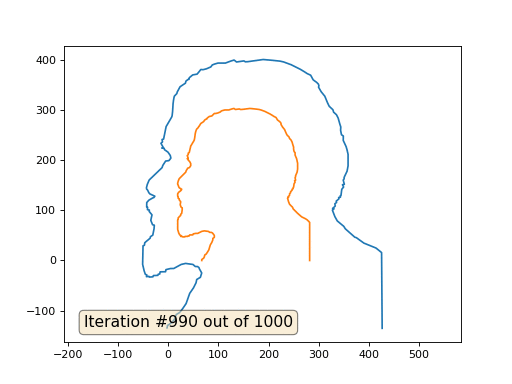
宿題：なぜ2番目のケースでは、レーニンは最初にジェルジンスキーに変わり、その後再びレーニンに収束しますが、サイズが大きくなりますか？

おわりに

多くのデータ処理タスク、特にジオメトリは、線形方程式系の解として定式化できます。この記事では、これらのシステムの構築方法については説明しませんでしたが、私の目標はこれが可能であることを示すことだけでした。次の記事のトピックは「理由」ではなく「方法」であり、後で使用するソルバーです。

ところで、結局のところ、記事のタイトルには最小二乗が含まれています。テキストでそれらを見ましたか？そうでない場合、これは絶対に怖くないです、これは「どのように？」という質問に対する答えです。次の記事では、彼らが隠れている場所と、それらを修正して非常に強力なデータ処理ツールにアクセスする方法を正確に示します。たとえば、10行のコードでこれを取得できます。

もっとお楽しみに！

涙と痛みのない最小二乗法