
最も一般的な進化方程式の1つを例として使用して微分方程式を解き、視覚化するスキルを強化します。古き良きScilabを思い出し、それが必要かどうかを理解しようとします。
julia>] (v1.0) pkg>update # (v1.0) pkg> status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.14.1+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0
そして問題の声明に進んでください
電磁界内の荷電粒子の動き
電荷を持つ荷電粒子上 EMFでの速度の移動 ローレンツ力の作用: 。 この式は、いくつかの簡略化で有効です。 相対性理論の修正を無視すると、粒子の質量は一定であると見なされるため、運動方程式は次の形式になります。
Y軸を電界に沿って、Z軸を磁場に沿って方向付け、簡単にするために初期粒子速度がXY平面にあると仮定します。 この場合、粒子の軌道全体もこの平面にあります。 運動方程式は次の形式を取ります。
測定不能: 。 アスタリスクは寸法の量を示し、 -検討中の物理システムの特性サイズ。 磁場中の荷電粒子の運動方程式の無次元システムを取得します。
順序を下げましょう:
モデルの初期構成として、次を選択します。 T V / m m / s 数値解法には、 DifferentialEquationsパッケージを使用します。
using DifferentialEquations, Plots pyplot() M = 9.11e-31 # kg q = 1.6e-19 # C C = 3e8 # m/s λ = 1e-3 # m function modelsolver(Bo = 2., Eo = 5e4, vel = 7e4) B = Bo*q*λ / (M*C) E = Eo*q*λ / (M*C*C) vel /= C A = [0. 0. 1. 0.; 0. 0. 0. 1.; 0. 0. 0. B; 0. 0. -B 0.] syst(u,p,t) = A * u + [0.; 0.; 0.; E] # ODE system u0 = [0.0; 0.0; vel; 0.0] # start cond-ns tspan = (0.0, 6pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, Euler(), dt = 1e-4, save_idxs = [1, 2], timeseries_steps = 1000) end Solut = modelsolver() plot(Solut)
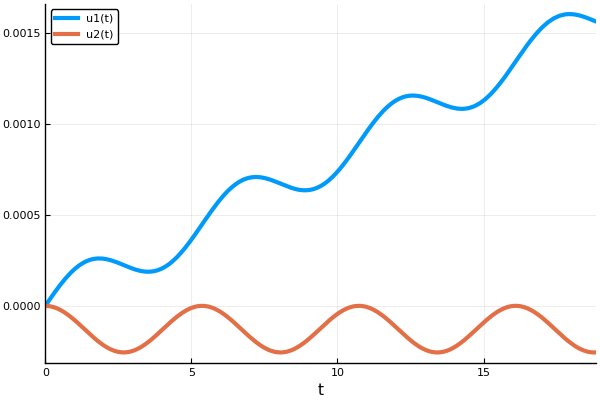
ここでは、ステップ数が指定されているオイラー法を使用します。 また、システムのソリューション全体が回答マトリックスに保存されるのではなく、1と2のインデックス、つまりXとプレーヤーの座標のみが保存されます(速度は必要ありません)。
X = [Solut.u[i][1] for i in eachindex(Solut.u)] Y = [Solut.u[i][2] for i in eachindex(Solut.u)] plot(X, Y, xaxis=("X"), background_color=RGB(0.1, 0.1, 0.1)) title!(" ") yaxis!("Y") savefig("XY1.png")#

結果を確認してください。 xの代わりに新しい変数を導入します 。 したがって、 X軸の方向に速度uで元の座標系に対して移動する新しい座標系に移行します。
選んだら そして示す 、システムは単純化されます:
電場は最後の等式から姿を消し、それらは均一磁場の影響下にある粒子の運動方程式です。 したがって、新しい座標系(x、y)の粒子は円を描くように移動する必要があります。 この新しい座標系自体は元の速度に対して相対的に移動するため 、パーティクルの結果の動きは、 X軸に沿った均一な動きと、 XY平面内の円の周りの回転で構成されます。 ご存知のように、これらの2つの動きが一緒に追加されるときに発生する軌道は、一般的な場合、 トロコイドです。 特に、初期速度がゼロの場合、この種の動きの最も単純なケースが実現します- サイクロイドに沿って。
ドリフト速度が実際にE / Vに等しいことを確認しましょう。 これを行うには:
- 最初の要素(最大)の代わりに意図的に低い値を設定することにより、応答行列を台無しにします
- 応答行列の2列目に最大要素の番号を見つけます。これは縦座標によって遅延されています
- 最大横座標値を対応する時間値で割ることにより、無次元ドリフト速度を計算します
Y[1] = -0.1 numax = argmax( Y ) X[numax] / Solut.t[numax]
アウト: 8.334546850446588e-5
B = 2*q*λ / (M*C) E = 5e4*q*λ / (M*C*C) E/B
出力: 8.33333333333333332e-5
7次まで!
便宜上、モデルのパラメーターとグラフの署名を受け取る関数を定義します。これは、プロジェクトフォルダーで作成されたpngファイルの名前としても機能します(Juno / AtomおよびJupyterで動作します)。 グラフがレイヤーで作成され、 plotsのplot()関数で表示されるGadflyとは異なり、1つのフレームで異なるグラフを作成するために、最初のグラフはplot()関数で作成され、後続のグラフはplot!()を使用して追加されます。 Juliaで受け入れられたオブジェクトを変更する関数の名前は、感嘆符で終わる慣習です。
function plotter(ttle = "qwerty", Bo = 2, Eo = 4e4, vel = 7e4) Ans = modelsolver(Bo, Eo, vel) X = [Ans.u[i][1] for i in eachindex(Ans.u)] Y = [Ans.u[i][2] for i in eachindex(Ans.u)] plot!(X, Y) p = title!(ttle) savefig( p, ttle * ".png" ) end
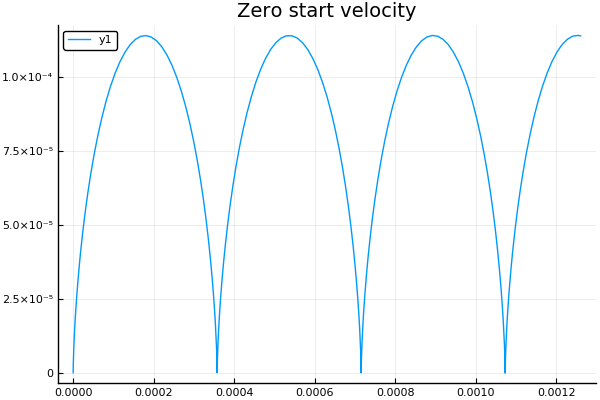
予想されるゼロ初期速度では、 サイクロイドを取得します。
plot() plotter("Zero start velocity", 2, 4e4, 7e4)
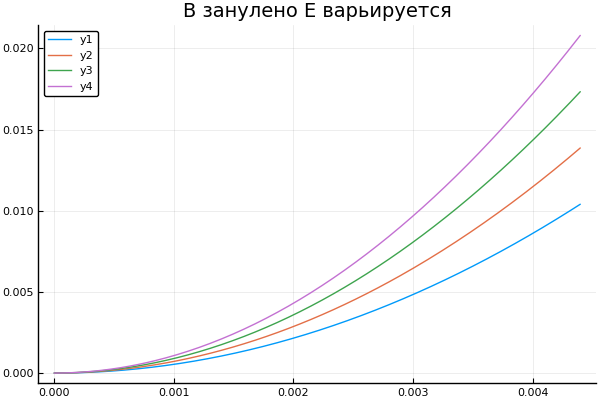
誘導、張力、および電荷符号が変化したときに、粒子の軌道を取得します。 ドットは、配列のすべての要素を使用して関数を順次実行することを意味します
plot() plotter.("B ", 0, [3e4 4e4 5e4 6e4] )
plot() plotter.("E B ", [1 2 3 4], 0 )

q = -1.6e-19 # C plot() plotter.(" ")
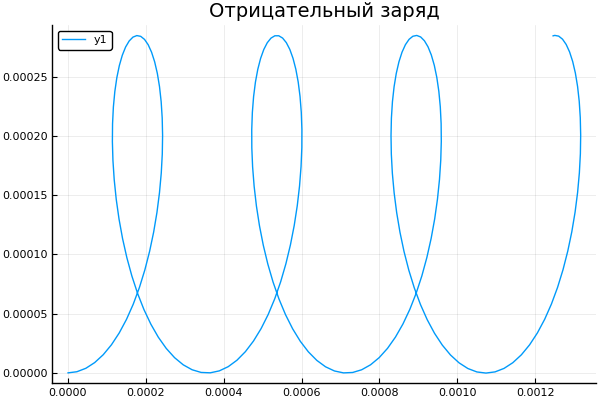
plot() plotter.(" ", 2, 5e4, [2e4 4e4 6e4 8e4] )
Scilabについて少し
Habréには、Silabに関する十分な情報(例1、2 )が既にあります。ここではOctaveについて 、 Wikipediaとホームページへのリンクに限定します 。
私自身で、チェックボックス、ボタン、グラフ、そしてかなり興味深いXcosビジュアルモデリングツールを備えた便利なインターフェイスの存在について追加します。 後者は、たとえば電気工学で信号をシミュレートするために使用できます。
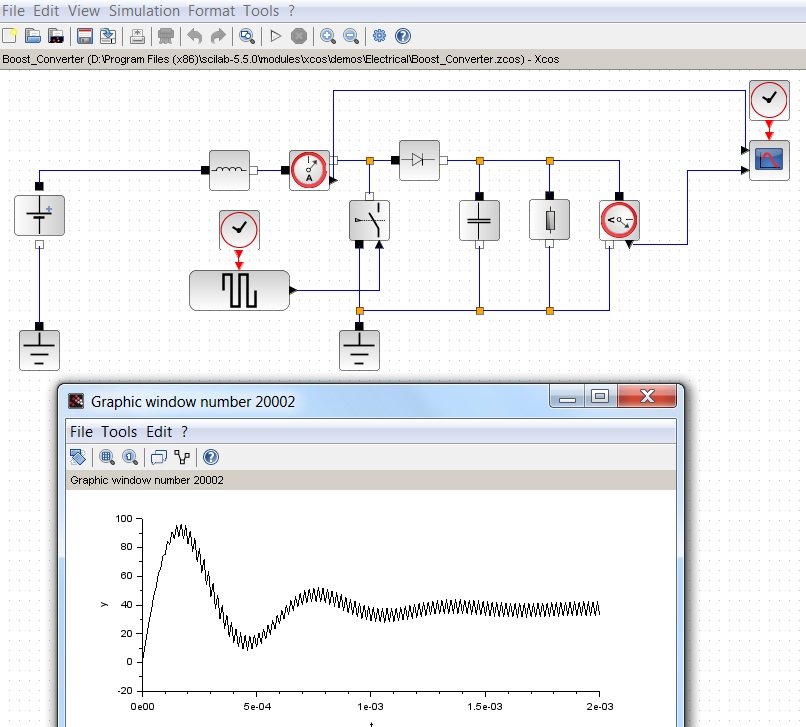

そして、これは非常に便利なガイドです:
実際、私たちの問題はScilabでも解決できます。
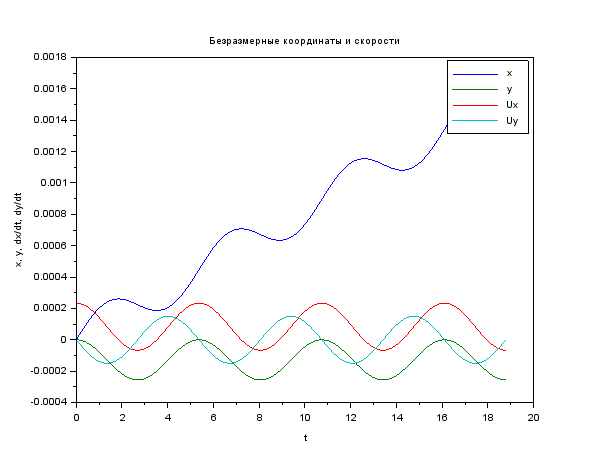
clear function du = syst(t, u, A, E) du = A * u + [0; 0; 0; E] // ODE system endfunction function [tspan, U] = modelsolver(Bo, Eo, vel) B = Bo*q*lambda / (M*C) E = Eo*q*lambda / (M*C*C) vel = vel / C u0 = [0; 0; vel; 0] // start cond-ns t0 = 0.0 tspan = t0:0.1:6*%pi // time period A = [0 0 1 0; 0 0 0 1; 0 0 0 B; 0 0 -B 0] U = ode("rk", u0, t0, tspan, list(syst, A, E) ) endfunction M = 9.11e-31 // kg q = 1.6e-19 // C C = 3e8 // m/s lambda = 1e-3 // m [cron, Ans1] = modelsolver( 2, 5e4, 7e4 ) plot(cron, Ans1 ) xtitle (" ","t","x, y, dx/dt, dy/dt"); legend ("x", "y", "Ux", "Uy"); scf(1)// plot(Ans1(1, :), Ans1(2, :) ) xtitle (" ","x","y"); xs2png(0,'graf1');// xs2jpg(1,'graf2');// , -

ここに ode diffursを解くための関数に関する情報があります。 原則として、質問は頼みます
なぜジュリアが必要なのですか?
... Scilab、Octave、Numpy、Scipyのような素晴らしいものがある場合は?
最後の2つについては言わない-私はそれを試していない。 そして一般的には質問は複雑なので、簡単に見てみましょう。
サイラブ
ハードドライブでは500 MBを少し超えるだけで、すぐに起動し、すぐに利用可能な差分計算、グラフィックス、その他すべてが利用可能になります。 初心者に適しています:優れたガイド(ほとんどローカライズされています)、ロシア語の本がたくさんあります。 内部エラーについては、 こことここですでに述べました。製品は非常にニッチであるため、コミュニティは低迷しており、追加のモジュールは非常に不足しています。
ジュリア
パッケージ(特にJupyterやMathplotlibなどのpythonフード)を追加すると、376 MBから6奇数ギガバイトになります。 彼女もRAMをspareしみません。132MBの開始時に、木星でスケジュールをプロットした後、静かに1 GBに達します。 Junoで作業する場合、すべてがScilabでの作業とほぼ同じです:インタープリターですぐにコードを実行でき、組み込みのメモ帳で印刷してファイルとして保存できます。変数ブラウザー、コマンドログ、オンラインヘルプがあります。 個人的には、clear()の欠如に dしています。つまり、コードを実行し、そこで修正して名前を変更し始めました。古い変数は残りました(Jupiterには変数ブラウザーはありません)。
しかし、これはすべて重要ではありません。 Scilabは最初のカップルに非常に適しています。額やカーソルを作成したり、その間の何かを計算することは非常に即興的なツールです。 並列計算とsishn / Fortran関数の呼び出しもサポートされていますが、それを真剣に使用することはできません。 大きな配列は彼を怖がらせ、多次元配列を設定するには、あらゆる種類の不明瞭さを処理する必要があり、古典的なタスクの範囲を超える計算は、OSとともにすべてを落とす可能性があります。
そして、これらすべての苦痛と失望の後、ここでも安全にJuliaに切り替えてレーキをかけることができます。 私たちは研究を続けます。コミュニティの利点は非常に反応が早く、問題はすぐに解決します。ジュリアには、学習プロセスをエキサイティングな旅に変える多くの興味深い機能があります!