グラフィックプログラマは、 クォータニオンを使用して3次元の回転を記録します。 ただし、 四元数は表面的に研究されているため、理解が困難です。 私たちは、奇妙な掛け算表やその他の不可解な定義を信仰に基づいて取り、必要に応じてベクトルを回転させる「ブラックボックス」として使用します。 なぜ M A 、T 、H 、B 、F 、I 2 = M 、A 、T 、H 、B 、F 、J 2 = M A T HのB F K 2 = - 1 そして m a t h b f i m a t h b f j = m a t h b f k ? なぜベクトルを取得し、それを「想像上の」ベクトルに変換して変換するのか、たとえば mathbfq(x mathbfi+y mathbfj+z mathbfk) mathbfq∗ ? しかし、誰もがすべてがうまくいくかどうか気にしますか?
ローターと呼ばれる回転を記述する方法があります。これは、複素数(2D)および四元数(3D)の場を指し、任意の数の次元に一般化します。
四元数を何もない状態から定義し、それらがどのように遡って機能するかを説明する代わりに、 ゼロからローターをほぼ完全に作成できます。 もっと時間がかかりますが、理解するのがはるかに簡単なので、私には価値があります!
さらに、3次元ローターの視覚化と理解のために、4番目の空間次元を使用する必要はありません。
彼らが四元数の使用と研究に取って代わり、ローターと交換し始めたら素晴らしいと思います。 それらを置き換えることは非常に簡単ですが、 コードはほぼ同じままです。 四元数でできること、たとえば、車軸ロック(ジンバルロック)の内挿と削除は、ローターでも実行できます。 しかし、私たちはより多くを理解し始めます。
(元の記事では、すべてのグラフがインタラクティブで、記事の後にビデオが続きます。再生ボタンをクリックすると、ビデオの対応するセクションを開始できます。ビデオの下の遷移ボタンをクリックして、記事の対応するセクションに移動することもできます。ウィンドウを拡大して、ビデオ用のスペースを増やします、または一定のサイズを設定します。)
1.ターニングプレーン
1.1。 ターンは2次元平面で実行されます。
3次元空間では、通常、軸上で回転する車輪のように、軸の周りで回転が発生していると認識しますが、車輪のある平面を表す方がより正確です。 この平面は軸に垂直です。

この老womanは飛行機の中で車輪を回します mathbfxz 軸に垂直 mathbfy 。
これは、ベクトルを2つの部分に分割し、そのうちの1つが平面( mathbfv parallel )、もう一方は外にあります( mathbfv perp )、回転により内側の部分が回転し、外側の部分は変更されません。

平面内の回転 yx [ 元の記事では、このアニメーションとカメラを移動できます ]
2次元空間では、回転が可能な平面は1つだけです( 外部部品はありません )。 したがって、回転が3番目の軸(2D平面に垂直)の周りで発生すると仮定するのは厳密に言えば正しくありません。回転を完了するために別の次元を追加するべきではないからです。
2次元の「平らな土地所有者」(2D平面内に住んでいて、2次元空間から出たことがない)に垂直回転軸について伝えると、「この軸はどの方向を向いているのか?」 私は彼女を想像できません!」
また、高次元(4D以上)では、2D平面に対する1つの法線ベクトルを決定できません(たとえば、4Dでは2D平面に2つの法線方向があり、5Dでは3つの法線方向があります。 nD 彼らの n−2 )
1.2。 ターンの正確な方向
さらに、軸を中心とした回転について考える場合、回転の方向は定義されていないため、ルール(いわゆる「右手ルール」)によって決定する必要があります。
ただし、平面内で回転が発生すると仮定すると、方向は明確になります。平面内の回転 mathbfxy (単位)ベクトルを移動する回転を意味します mathbfx (ユニット)ベクトル mathbfy 飛行機の中で彼らは一緒に形成します。 平面内の回転 mathbfyx 逆方向の回転:ベクトルを移動します mathbfy ベクトルへ mathbfx 。
直交平面に沿った3D回転の3つのマトリックスについて初めて学んだとき、私は最初に考えました:地獄はマトリックスである mathbfRy 反対の記号がありますか? これは右手の規則によるものであり、それに応じて軸の周りの回転を決定する必要があります mathbfy から実行されるように mathbfz に mathbfx からではない mathbfx に mathbfz 一定の「右」回転方向を維持するため。 飛行機自体について直接話し始めると、このルールは不要になります。
R_X(\ theta)= \ begin {bmatrix} 1&0&0 \\ 0&cos(\ theta)&-sin(\ theta)\\ 0&sin(\ theta)&cos(\ theta)\ end {bmatrix} \:\:\:R_Y(\ theta)= \ begin {bmatrix} cos(\ theta)&0&\ bbox [5px、border-bottom:2px solid red] {\ \} sin(\ theta) \\ 0&1&0 \\ \ bbox [5px、border-bottom:2px red red] {-} sin(\ theta)&0&cos(\ theta)\ end {bmatrix} \:\:\:R_Z (\ theta)= \ begin {bmatrix} cos(\ theta)&-sin(\ theta)&0 \\ sin(\ theta)&cos(\ theta)&0 \\ 0&0&1 \ end {bmatrix }
R_X(\ theta)= \ begin {bmatrix} 1&0&0 \\ 0&cos(\ theta)&-sin(\ theta)\\ 0&sin(\ theta)&cos(\ theta)\ end {bmatrix} \:\:\:R_Y(\ theta)= \ begin {bmatrix} cos(\ theta)&0&\ bbox [5px、border-bottom:2px solid red] {\ \} sin(\ theta) \\ 0&1&0 \\ \ bbox [5px、border-bottom:2px red red] {-} sin(\ theta)&0&cos(\ theta)\ end {bmatrix} \:\:\:R_Z (\ theta)= \ begin {bmatrix} cos(\ theta)&-sin(\ theta)&0 \\ sin(\ theta)&cos(\ theta)&0 \\ 0&0&1 \ end {bmatrix }
2.バイベクトル
2.1。 外部作業
1つのベクトルを回転させるときに回転軸を計算するには mathbfa 別のベクトルへ mathbfb 2つのベクトルのベクトル積を取り、両方のベクトルに垂直なベクトルを取得します。 しかし、回転が本質的に2次元の操作である場合、なぜ平面を「残す」必要があるのでしょうか。
代わりに、 外部積 (2次元ベクトル積とも呼ばれます)と呼ばれるもの、2つのベクトルを取り、「バイベクトル」(または2ベクトル)と呼ばれる新しい要素を作成します mathbfB 2つのベクトルが一緒に形成される平面を表します。 ベクトル積が平面への法線ベクトルを作成する場合 、外部積は平面自体を作成します 。 平面の法線の計算は無関係です。
mathbfB= mathbfa\ウェッジ mathbfb
mathbfB ベクトルから構築された平行四辺形として表すことができます mathbfa そして mathbfb 彼らが一緒に形成する平面で。
最初は、バイベクトルの考え方は奇妙に思えるかもしれませんが、すぐに、ベクトル自体とほぼ同じ基本的なものであることがわかります。 ベクトルを直線と比較できる場合、バイベクトルは平面のようになります...外部製品のプロパティは、平面の重要なプロパティをキャプチャします。
2.2。 バイベクトルの基礎

ベクトルのようなバイベクトルにはコンポーネントがあります。 しかし、それらはベクトルのような直線ではなく、 平面に基づいて決定されます。
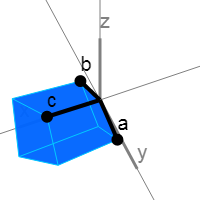
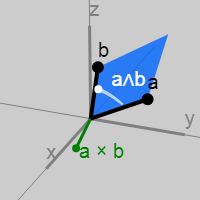
3つの直交する底面は mathbfx\くさび mathbfy 、 mathbfx\くさび mathbfz そして mathbfy\くさび mathbfz 図からわかるように。
しかし、最初に、より単純な2次元のケースを見てみましょう...
2.3。 二次元バイベクトル
2Dでは、プレーンは1つだけです。つまり、 mathbfxy 。 つまり、2次元のバイベクトルには1つのコンポーネントしかありません。 ベクトルで構成されるバイベクトルの場合 mathbfa そして mathbfb 数です Bxy 2つのベクトルで形成される平行四辺形の面積(符号付き)に等しい。
mathbfB= mathbfa\くさび mathbfb=Bxy( mathbfx\くさび mathbfy)
2D bivectorを使用した元の記事では、構成されている(単一の)ベクトルを変更することにより、インタラクティブグラフを試すことができます。
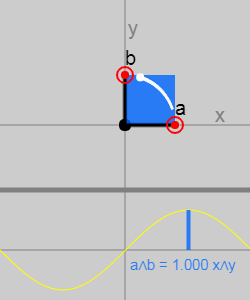
ベクトル間の角度が変化すると、平行四辺形の領域が変化することがわかります(角度のサインに従って)。
ベクトルが同じまたは平行である場合、それらは通常の平面を形成せず、結果はゼロになります。 この単純なプロパティは、バイベクトルとは何かを定義します。
mathbfa\くさび mathbfa=0
2つのベクトルの合計を見ると、プロパティが次のようになっていることがわかります。
begineqnarray( mathbfa+ mathbfb)\楔( mathbfa+ mathbfb)&=&0 mathbfa\くさび mathbfa+ mathbfb\くさび mathbfa+ mathbfa\くさび mathbfb+ mathbfb\くさび mathbfb&=&0 mathbfb\ウェッジ mathbfa+ mathbfa\ウェッジ mathbfb&=&0 endeqnarray
したがって:
mathbfa\くさび mathbfb=− mathbfb\くさび mathbfa
回転の方向と同様に、外部作業の引数の順序が重要です。 引数の順序を変更すると、結果の符号が変更されます(これを「非対称」と呼びます)。
チャートでは、サインは青から緑に変わる色で示されます。 のターン時にサインが変わります mathbfa で mathbfb 時計回りから反時計回りに移動します(つまり、方向と一致する場合(から mathbfx に mathbfy )または方向(from mathbfy に mathbfx ))。
外部製品のプロパティは、飛行機とターンのプロパティを伝えるように配置されていることがわかります。
2.4。 非単位ベクトルの2次元バイベクトル
明らかに、ベクトルは単位長である必要はなく、このグラフのこの制限は削除されました。

符号付きの平行四辺形の面積は、両方のベクトルの長さに比例します。 Bxy=sin( alpha) |a | |b | どこで alpha 間の角度は mathbfa そして mathbfb 。 つまり、たとえば、1つのベクトルの長さを2倍にすると、面積が2倍になります。
ベクトルをコンポーネントとして置き換えることにより、真の値を取得できます。
begineqnarray mathbfa\くさび mathbfb&=&(ax mathbfx+ay mathbfy)\くさび(bx mathbfx+by mathbfy)&=&axbx( mathbfx\くさび mathbfx)+axby( mathbfx\くさび mathbfy)+aybx( mathbfy\くさび mathbfx)+ayby( mathbfy\くさび mathbfy)&=&axby( mathbfx\くさび mathbfy)+aybx( mathbfy\くさび mathbfx)&=&axby( mathbfx\くさび mathbfy)−aybx( mathbfx\くさび mathbfy)&=&(axby−aybx)( mathbfx\ウェッジ mathbfy) endeqnarray
Bxy=axby−bxay
2.5。 3Dバイベクトル

ベクトル座標と同じ mathbfv 3つの直交基底軸上のベクトルの射影と考えることができます( mathbfx 、 mathbfy 、 mathbfz )、バイベクトルの座標 mathbfB 3つの直交する基底面上の平面より小さい投影と見なすことができます。
ベクトルの射影は各基底ベクトルに沿ったこのベクトルの長さであり、バイベクトルの射影は各基底平面上の平面の領域です 。
ベクターの場合:
mathbfv= bbox[5px、border−bottom:2pxsolidred]vx mathbfx+ bbox[5px、border−bottom:2pxsolidgreen]vy mathbfy+ bbox[5px、border−bottom:2pxsolidblue]vz mathbfz
バイベクトルの場合:
mathbfB= bbox[5px、border−bottom:2pxsolidcoral]Bxy( mathbfx\楔 mathbfy)+ bbox[5px、border−bottom:2pxソリッドゴールド]Bxz( mathbfx\ウェッジ mathbfz)+ bbox[5px、border−bottom:2pxソリッドダークバイオレット]Byz( mathbfy\くさび mathbfz)
どこで Bxy 、 Bxz 、 Byz のような数字だけです vx 、 vy 、 vz (グラフ上の色に対応する色で下線が引かれています)。
3Dバイベクターのコンポーネントは、基本的な2D平面へのバイベクターの3つの2D投影です。
前と同じ方法を使用すると、コンポーネントの真の値は2次元の場合のXYコンポーネントに非常に似ていますが、3つの平面すべてに適用されることがわかります。
Bxy=axby−bxay
Bxz=axbz−bxaz
Byz=aybz−byaz
元の記事のインタラクティブチャートで3Dバイベクトルを試すことができます。
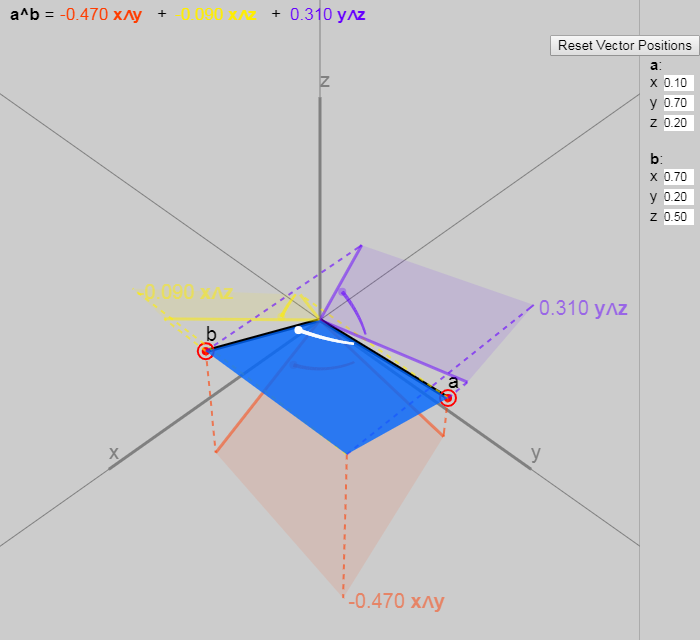
バイベクトルのノルム | mathbfB |= | mathbfa\ウェッジ mathbfb | は、ベクトルのノルム(成分の平方和の平方根)と同様に決定されます。 これは、形成された平行四辺形の面積に等しい mathbfa そして mathbfb 、つまり | mathbfa\ウェッジ mathbfb |= midsin( alpha) mid | mathbfa | | mathbfb | どこで alpha -間の角度 mathbfa そして mathbfb 。
バイベクトルをそのノルムで除算すると、ベクトルの2つの長さと角度のサインの(絶対)値が減ります。つまり、バイベクトルが得られます。 hat mathbfB 、2つのベクトルが元々垂直で、単位の長さを持っているかのように構築されます。 これは、両方のベクトルを含む平面の非常にきれいな表現です。 だから:
mathbfB=| mathbfa | ||mathbfb | midsin( alpha) mid hat mathbfB
何か外部の仕事を思い出させますか? 3Dでは、外部作品の定義はベクター作品の定義に非常に似ています。 実際、ベクトル積(たとえば、法線ベクトル)から取得した3Dのベクトルには、バイベクトルの成分と等しい3つの成分があります(数値は同じですが、基底は異なります)。
$$表示$$ \開始{eqnarray} \ mathbf {a} \くさび\ mathbf {b}&=&&(a_x b_y-b_x a_y)(\ mathbf {x} \くさび\ mathbf {y})\\& &+&(a_x b_z-b_x a_z)(\ mathbf {x} \くさび\ mathbf {z})\\&&+&(a_y b_z-b_y a_z)(\ mathbf {y} \くさび\ mathbf {z} )\\ \\ \ mathbf {a} \ times \ mathbf {b}&=&&(a_x b_y-b_x a_y)\ \ mathbf {z} \\&&--(a_x b_z-b_x a_z)\ \ mathbf {y} \\&&+&(a_y b_z-b_y a_z)\ \ mathbf {x} \ end {eqnarray} $$ display $$
バイベクトルの定義には幾何学的な意味があり、どこからともなく現れることはありません。 ベクトル積を調べたとき、「これらの2つのベクトルによって形成される平行四辺形の面積に等しい長さのベクトルを返すのは一体何なのか?」 それはとてもランダムに思えます。 そして、なぜ平行四辺形の領域をベクトルの長さに変えることができるのでしょうか?」
2.6。 ベクトルとバイベクトルの意味論
3Dでは、バイベクトルには平面ごとに1つずつ、合計3つの座標があります:( mathbfxy 、 mathbfxz そして mathbfyz ) ベクトルには、軸ごとに1つの3つの座標もあります( mathbfx 、 mathbfy そして mathbfz ) 各平面は1つの軸に垂直です。 この偶然の一致は3次元(*)でのみ発生するため、バイベクトルとベクトルを常に混同する理由です。
2Dでは、基本的なバイベクトルは1つだけです( mathbfxy )、および3Dには3つの基底バイベクトル( mathbfxy 、 mathbfxz 、 mathbfyz )、4Dには6つの基底バイベクトル( mathbfxy 、 mathbfxz 、 mathbfxw 、 mathbfyz 、 mathbfyw 、 mathbfzw )など...
プログラミングでは、どちらもメモリレイアウトは同じですが、操作が異なります。 3Dバイベクトルの代わりに3Dベクトルを使用することは、バイベクトルの「型変換」に似ています。
例は次のとおりです。「逆転送」行列を使用して、法線ベクトルが通常のベクトルとは異なる方法で変換されることがわかります。 ( mathbfMT)−1 、マトリックス自体の代わりに。 これは、実際には、実際にはベクトルではなく、「型変換によるベクトル」に変換されるバイベクトルであるためです。 物理学では、「軸ベクトル」と呼ばれるハックがあります。これは、ベクトル積によって得られるベクトルを通常のベクトルと区別するために導入されました。 バイベクトルはオブジェクトの真の「タイプ」であり、それに応じて認識および処理する必要があります。
引き続き、外部製品を使用して、方向付けられた2Dエリアだけでなく、方向付けられた3Dボリュームも取得できます。 トライベクトル T 外部製品を2回実行することで取得できます。
mathbfT= mathbfa\くさび mathbfb\くさび mathbfc
三次元空間では、すべてがそこで終わります。 2Dスペース全体を埋める平面が1つしかない2Dのように、3Dスペースも3Dスペース全体を埋めるボリュームは1つだけです。
[しかし、nDでは、n番目の次元に達するまで、さらに大きな外部積ベクトルを作成し続けることができます。 たとえば、4Dでは、4つの基底トリブクター(3ベクトル)( mathbfxyz 、 mathbfxyw 、 mathbfxwz 、 mathbfyzw )および1つの基本的な4ベクトル mathbfxyzw ]
3Dでは、trivectorには1つの基本的なコンポーネント( Txyz )3つのベクトルによって形成される平行六面体の体積に等しい。 トリプル外積は、スカラートリプル積の改良バージョンです( ( mathbfa times mathbfb) cdot mathbfc )、1つのタイプの操作のみを含むため、正しいタイプ(スカラーではなくボリューム)を返し、任意の数の次元で機能します。
mathbfT=Txyz mathbfx\ウェッジ mathbfy\ウェッジ mathbfz
3.幾何積
3.1。 互いにベクトルの乗算
幾何積 mathbfab (記号なしで表示)は、ベクトルを使用して実行できる別の操作です。 幾何積は、ベクトルが逆になるように定義されます(たとえば、 mathbfa mathbfa−1=1 、ここで1は単なる数字の1!)であり、たとえば結合性( mathbfa( mathbfb mathbfc)=( mathbfa mathbfb) mathbfc ) これの目的は、(行列の場合のように)乗算が幾何学的演算に対応するようにベクトルを乗算できるようにすることです。
オブジェクトが何であれ、逆の値を使用すると便利です。 mathbfa mathbfa−1 、ベクトルには影響しません。つまり、数値を1倍したときと同じように動作します。
作品を定義するために、まず、作品(または2つの引数を取る関数)を、引数を交換しても変わらない部分と次のように変化する部分の合計に分割できることに注意してください。
begineqnarray mathbfa mathbfb&=& frac12( mathbfa mathbfb+ mathbfa mathbfb+ mathbfb mathbfa− mathbfb mathbfa)&=& frac12( mathbfa mathbfb+ mathbfb mathbfa)+ frac12( mathbfa mathbfb− mathbfb mathbfa) endeqnarray
最初のメンバーは引数の順序に依存しなくなりました mathbfa そして mathbfb (「対称」部分と呼ばれます)、2番目の用語は、引数の場所を変更するときに符号を変更します(「非対称」部分と呼ばれます)。
2つのベクトルのスカラー積(内部積とも呼ばれる)は対称であり、距離の尺度( mathbfa cdot mathbfa= | mathbfa |2 )、したがって、幾何学的な観点から、対称部分と等しくすることが有用であると思われます:
frac12( mathbfa mathbfb+ mathbfb mathbfa)= mathbfa cdot mathbfb
同様に、2つのベクトルの外積は非対称であるため、非対称部分と同一視すると便利です。
frac12( mathbfa mathbfb− mathbfb mathbfa)= mathbfa\くさび mathbfb
さらに、スカラー積には2つのベクトル間の角度のコサインが含まれます( mathbfa cdot mathbfb= | mathbfa | | mathbfb |cos( alpha) )、外部製品には角度のサインが含まれています。 一緒に、それらはベクトル間の角度とそれらが形成する平面を完全に記述します。
仕事に含まれる情報の助けを借りて、あるベクターから別のベクターに行くことができるので、仕事を可逆にするのは記述の完全性です。 あげたら mathbfa そして mathbfa mathbfb その後、あなたは得ることができます mathbfb 。 コサインのみ、またはサイン/プレーンのみを知っているため、これは不可能です。
つまり、幾何積は次と等しくなります。
mathbfa mathbfb= mathbfa cdot mathbfb+ mathbfa\くさび mathbfb
2つのベクトルを乗算すると、スカラーとバイベクトルという2つの異なるものの合計が得られるため、これは奇妙です。 ただし、これは複素数がスカラーと「虚数」の合計であることに似ているため、すでに慣れている可能性があります。 ここで、バイベクトル部分は、複素数の「虚数」部分に対応します。 これだけが「想像上の」値ではなく、単にグラフィカルに表示できるバイベクトルです。
実際、2つのベクトルを乗算して、それらの有用なプロパティ(「互いへの投影の長さ」/「角度の余弦」( m a t h b f a c d o t m a t h b f b )および「それらが一緒に形成する平面」/「角度のサイン」( メートルトンの時間B F A \くさんびメートルトンの時間B F B 私たちはと結合))、 "プラス。" 幾何積は、それらに適用できる「プロパティグループ」の操作も提供し、これらの操作には幾何学的な解釈があります(たとえば、ベクトルの回転と反射)。これはすぐに表示されます。
サインとコサインで幾何積を表現できます:ab=‖a‖‖b‖(cos(α)+sin(α)B) どこで B 2つの単位垂直ベクトルで構成される、平面内の両方のベクトルのバイベクトルです。
3.2。 乗算表
乗算表を使用すると、積をより具体的にすることができます。基底ベクトルの積を取得するとどうなるか見てみましょう( x 、 y 、 z )
任意の基底ベクトル、たとえば軸 x 、結果は等しくなります 1 :
xx=x⋅x+x∧x=1
基底ベクトルの任意のペア、たとえば軸 x そして y 、結果はバイベクトルになり、それらが一緒に形成されます:
xy=x⋅y+x∧y=x∧y
(つまり、名前を付けることができます x∧y ただ xy、
これはまったく同じなので!)これにより、次の表が得られます。
| ab | b | |||
| x | y | z | ||
| a | x | 1 | xy | xz |
| y | −xy | 1 | yz | |
| z | −xz | −yz | 1 | |
実際、この表は、たとえば、四元数の表と比較すると簡単です。
, (5,3,0) そして (2,0,1) :
(5x+3y)(2x+1z)=5 2 xx+5 1 xz+3 2 yx+3 1 yz=10+5 xz−6 xy+3 yz
3.3。 反射式(従来の外観)

ベクトルへの反映[元の記事では、各ベクトルを移動できます]
単位ベクトルがある場合a およびベクトル mathbfv 私たちは反映することができます mathbfv 垂直な平面を通して a 。
これは通常の方法で行われます:私たちは共有します mathbfv 平面に垂直な部分: v⊥=(v⋅a)a 、および平面に平行な部分: v∥=v−v⊥=v−(v⋅a)a 。
次に、ベクトルを反映するために、垂直部分を反転し、平行部分を変更せずに残します。
Ra(v)=v∥−v⊥=(v−(v⋅a)a)−((v⋅a)a)=v−2(v⋅a)a
3.4。 反射の式(幾何積のビュー)
この段階で、スカラー積を置き換えることができます v⋅a 幾何学的な製品の形のバージョン 12(va+av) 、および以下を取得します。
Ra(v)=v−2(12(va+av))a=v−va2−ava=−ava
( a2=a⋅a=1 以来 a
これは単一のベクトルです)これはまったく同じことですが、異なるレコードにあります。リフレクションなどの基本的な操作をエンコードするための式ではなく、単純な製品の形式でレコードを使用すると非常に便利です!
, , . :
x(xx)=x1=xx(xy)=x(x⋅y+x∧y)=x(x⋅y)+xxy=x(x⋅y)+yx(yz)=x(y⋅z)+xyz
結果は次のようになります:vector、vector、vector + trivector。 ただし、後者の場合は、3つのベクトルすべてが独立している場合にのみ発生します。 − mathbfava
好奇心people盛な人は、各段階で何が起こるかを見ることができます。 − mathbfa mathbfv mathbfa 幾何積の観点から。
- 第一段階:
mathbfv mathbfa= mathbfv cdot mathbfa+ mathbfv\ウェッジ mathbfa
前と同じように分割すると mathbfv 平面に垂直な部分( mathbfv perp )、およびそれに平行な部分( mathbfv parallel )、取得します:
begineqnarray( mathbfv perp+ mathbfv parallel) mathbfa&=&( mathbfv perp+ mathbfv parallel) cdot mathbfa+( mathbfv perp+ mathbfv parallel) edge mathbfa&=& mathbfv perp cdot mathbfa+ mathbfv parallel cdot mathbfa+ mathbfv perp edge mathbfa+ mathbfv parallel edge mathbfa endeqnarray
mathbfv parallel cdot mathbfa=0 、これらのベクトルは垂直であり、 mathbfv perp edge mathbfa=0 これらのベクトルは平行だからです。
mathbfv mathbfa= mathbfv perp cdot mathbfa+ mathbfv parallel\くさび mathbfa
最初の項は、投影の長さです mathbfv に mathbfa 、つまり 最初の項はちょうど長さです mathbfv perp 。
電話しましょう hat mathbfv parallel 正規化バージョン mathbfv parallel それは mathbfv parallel= hat mathbfv parallel | mathbfv parallel | 。 その場合、2番目の項は単なるバイベクトルです mathbfB= hat mathbfv parallel\くさび mathbfa 長さの倍 mathbfv parallel 。
このバイベクトル mathbfB 2つの垂直な単位ベクトルで構成されています。つまり、これはベクトル平面の非常にきれいな表現です。 mathbfa そして mathbfv 。 相対的な角度や長さに関する情報は含まれず、平面の向きのみが含まれます。
つまり、両方の用語は単に分解です mathbfv 2つの直交射影( mathbfv parallel そして mathbfv perp )、およびそれらが形成する平面( mathbfB ):
| mathbfv perp |+ | mathbfv parallel | mathbfB
次のステップに進む前に、外部製品を幾何学的製品に置き換えることができます。 mathbfa そして mathbfv parallel は垂直であるため、それらの外部積と幾何積は同等になります(幾何積からのスカラー積を持つ部分はゼロに等しいため)。
mathbfv perp cdot mathbfa+ mathbfv parallel edge mathbfa= mathbfv perp cdot mathbfa+ mathbfv parallel mathbfa
- 第2段階は次のとおりです。
mathbfa mathbfv mathbfa= mathbfa( mathbfv perp cdot mathbfa)+ mathbfa mathbfv parallel mathbfa
最初のメンバーは単なるコンポーネントです mathbfv に沿って mathbfa 、つまり 成分 mathbfv 平面に垂直。 つまり、最初の用語は mathbfv perp 。
mathbfa mathbfv mathbfa= mathbfv perp+ mathbfa mathbfv parallel mathbfa
以来 mathbfa そして mathbfv parallel (再び)垂直、それらの幾何積は単純に外部積です。つまり、それらを交換して記号を変更できます。
begineqnarray mathbfa mathbfv mathbfa&=& mathbfv perp− mathbfv parallel mathbfa mathbfa&=& mathbfv perp− mathbfv parallel endeqnarray
- そして最後に、最後の段階で記号が反転します。
− mathbfa mathbfv mathbfa=− mathbfv perp+ mathbfv parallel
つまり、コンポーネントが mathbfv 平面に垂直、上下逆さまになっていますが、平行部分は同じままです!
長さ mathbfa それほど重要ではないため、以下では無視しますが、 mathbfa は単位ベクトルではないため、その長さで除算する必要があり、式は - M A T H B F A M A T H B 、F 、V、M 、A 、T HのB F - 1 、これはあなたが慣れているはずの「レイヤード製品」に似ています。
3.5。 2つの反射が順番です:2Dの状況
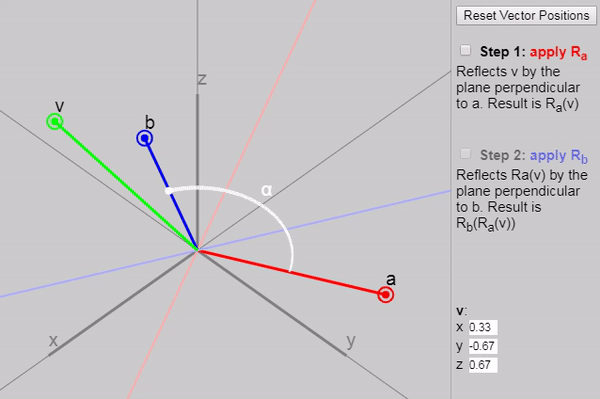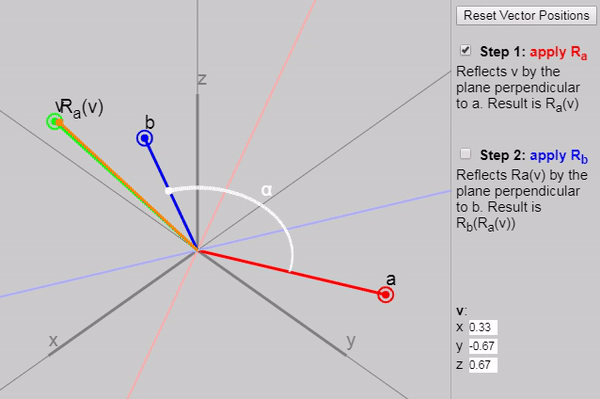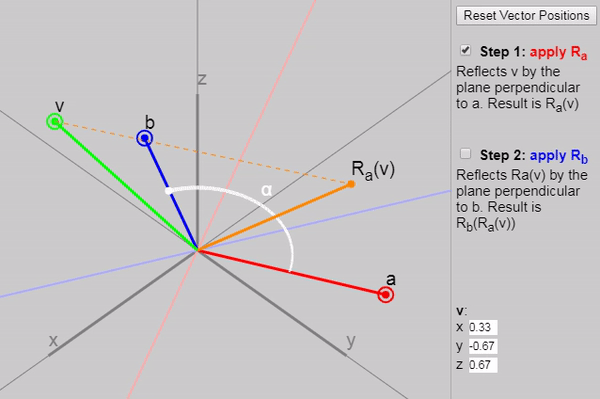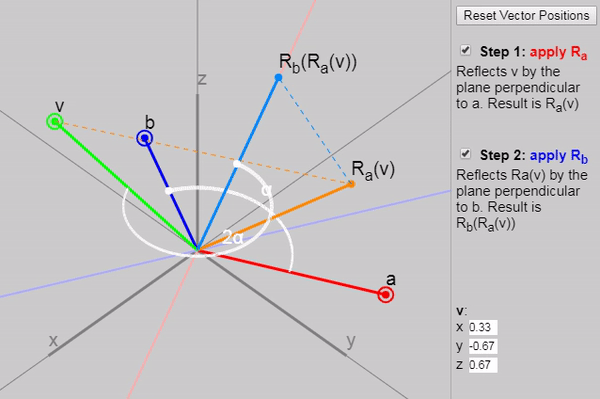
に適用すると mathbfv 2つの連続した反射(最初はベクトル mathbfa そして、ベクトルで mathbfb )、 ベクトル間の角度の2倍の回転を取得します mathbfa そして mathbfb 。
以下のグラフに、反射の各後続段階を示します。
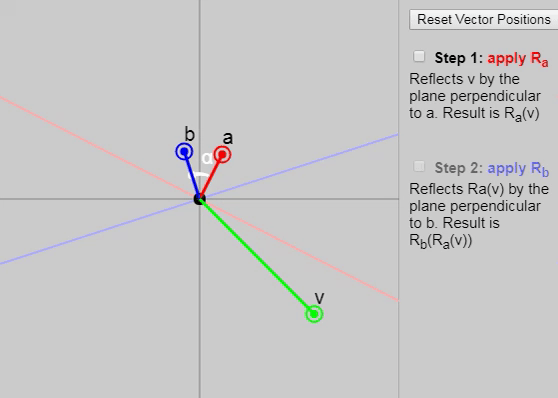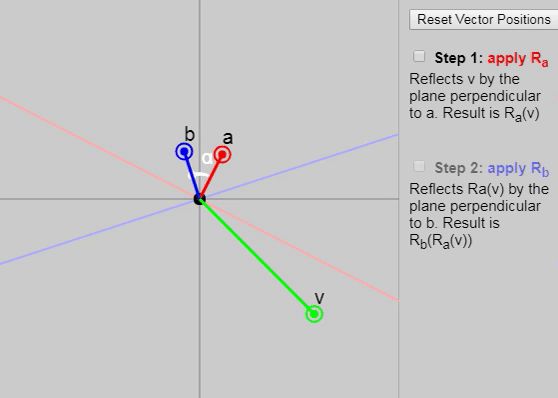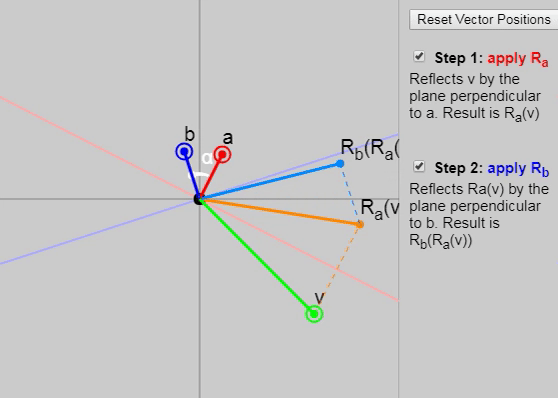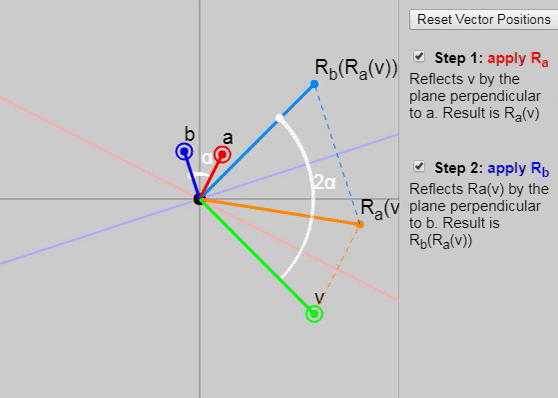
また、元の記事では、ベクトルを変更できます mathbfa 、 mathbfb そして mathbfv ただし、グラフ上のベクトルの初期設定([ベクトル位置のリセット]ボタンをクリック)は、結果として回転が二重の角度で発生する理由を特に明確に示しています。 別の適切な構成は次のように設定することです mathbfa そして mathbfb 軸 mathbfx そして mathbfy 。
3.6。 2つの反射が順番です:3Dの状況
3Dベクトルの場合 mathbfv 2つの部分に分けることができ、そのうちの1つは与えられた平面にあります mathbfa そして mathbfb 、もう1つは平面の外側にあります(垂直)。 下のグラフに示すように、ベクトルが各プレーンで反射される場合、その外側部分は同じままです。 内側については、2Dに戻り、角度が2倍になります!

3.7。 ローター
幾何積の観点から見ると、2つの反射は単純に次のものに対応します。
R mathbfb(R mathbfa( mathbfv))=− mathbfb(− mathbfa mathbfv mathbfa) mathbfb= mathbfb mathbfa\: mathbfv\: mathbfa mathbfb
呼ぶ mathbfa mathbfb= mathbfa cdot mathbfb+ mathbfa\くさび mathbfb ローター mathbfa mathbfb ベクトルの両側で、回転( mathbfb mathbfa と同じです mathbfa mathbfb 、反転部分バイベクトルのみ)。
ローターアプリケーション mathbfa mathbfb ベクトルの両側に、ベクトルの平面でこのベクトルを回転させます mathbfa そして mathbfb 間の角度の2倍 mathbfa そして mathbfb 。
そしてそれだけです!
3Dローターとクォータニオンの比較
3Dローターはクォータニオンによく似ていることがわかります。
a+Bxy mathbfx\くさび mathbfy+Bxz mathbfx\くさび mathbfz+Byz mathbfy\くさび mathbfz
a+b mathbfi+c mathbfj+d mathbfk
実際、コード/数学はほとんど同じです! 主な違いは mathbfi 、 mathbfj そして mathbfk に置き換えられました mathbfy\くさび mathbfz 、 mathbfx\くさび mathbfz そして mathbfx\くさび mathbfy しかし、それらは基本的に同じように機能します。 コードの比較はこちらにあります 。 たとえば、補間のためのlog / expなど、すべてを実装したわけではありませんが、作成は非常に簡単です。
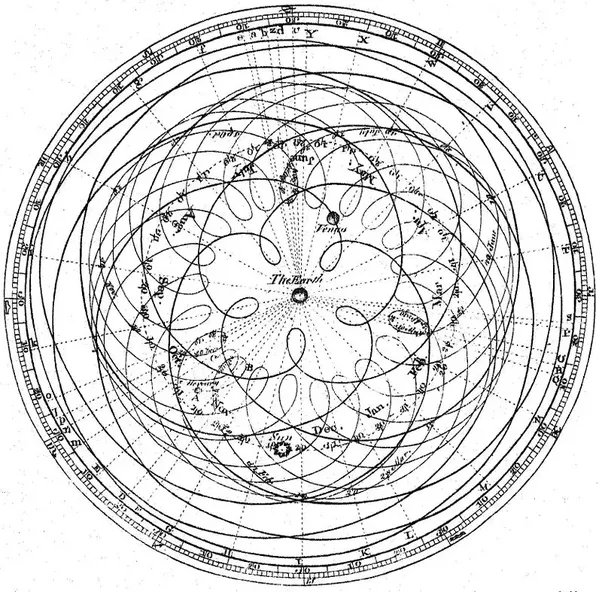
ただし、これまで見てきたように、3Dローターは3次元の概念であり、視覚化に「4次元の二重回転」や「立体投影」を使用する必要はありません。 4Dで動作するクォータニオンを視覚化して3D回転を説明することは、地球中心の観点から惑星の動きを理解しようとすることに似ています。 つまり このアプローチは、見方が間違っているため複雑すぎます。
見てきたように、回転をベクトルの周りではなく平面の内側で発生するようにモデリングすると、非常に役立ちます。 たとえば、基本バイベクトルの二乗は、 −1 、基本的なクォータニオン( mathbfi2= mathbfj2= mathbfk2=−1 ):
( mathbfx mathbfy)2=( mathbfx mathbfy)( mathbfx mathbfy)=−( mathbfy mathbfx)( mathbfx mathbfy)=− mathbfy( mathbfx mathbfx) mathbfy=− mathbfy mathbfy=−1
2つのバイベクトルを互いに乗算すると、3番目のバイベクトルが得られますが、実際には簡単であり、それを覚えておく必要はありません mathbfi mathbfj= mathbfk :
( mathbfx mathbfy)( mathbfy mathbfz)= mathbfx( mathbfy mathbfy) mathbfz= mathbfx mathbfz
(使用したことに注意してください mathbfx\くさび mathbfy= mathbfx mathbfy )
これらの特性は幾何積の結果であり、どこからともなく発生するものではありません!
追加の読書
(ところで、幾何学的代数にはローターだけでなく、他のクールなものもあります!)
- マクドナルドの線形代数幾何 [ Amazonへのリンク ]
学生にとって線形代数の教科書に取って代わることが暗示されているため、非常に明確で理解しやすい優れた情報源。 - Dorst et al。によるコンピューターサイエンスの幾何学的代数 [ Amazonへのリンク ]
優れたソース。プログラミングにより、主題をよりよく理解できる場合があるからです。注:この本では、著者は幾何学的代数が四元数より遅いことを明らかにしています(など)。 実際、ほぼ同じコードを持つ必要があります(つまり、幾何代数のコードを記述してはいけません。可能なすべてのタイプのkベクトルを含むことができる一般化された構造体を作成し、必要に応じて、各タイプのkベクトルに1つの構造体を書くだけですつまり、クォータニオンを置き換えるには、1つのBivector構造と1つのRotor構造(スカラー+ Bivector)を記述できます。