変分自動エンコーダー（自動エンコーダー）は、特定の隠された空間にオブジェクトを表示することを学習する生成モデルです。



変分オートエンコーダー（VAE）モデルがどのように機能するか疑問に思ったことはありませんか？ VAEがトレーニングされたデータセットのような新しい例をどのように生成するか知りたいですか？ この記事を読んだ後、VAEの内部動作の理論的な理解が得られます。また、自分で実装することもできます。 次に、手書きの数字のセットでトレーニングされた作業VAEコードを示します。新しい数字を生成する楽しみがあります。

生成モデル

VAEは生成モデルであり、トレーニングデータの確率密度（PDF）を推定します。 そのようなモデルが自然画像で訓練されている場合、ライオンの画像に高い確率値を割り当て、ランダムなでたらめの画像に低い値を割り当てます。



VAEモデルは、トレーニング済みのPDFからサンプルを取ることもできます。これは、元のデータセットに似た新しいサンプルを生成できるため、最もクールな部分です。



MNIST手書き番号セットを使用したVAEについて説明します。 モデルの入力データは、形式の画像です $$$\ mathbb {R} ^ {28×28}$ 。 モデルは、入力が数字のように見える可能性を評価する必要があります。

画像モデリングタスク

ピクセル間の相互作用は難しいタスクです。 ピクセルが互いに独立している場合、各ピクセルのPDFを個別に調べる必要がありますが、これは簡単です。 選択も簡単です-各ピクセルを個別に取得します。



しかし、デジタル画像では、ピクセル間に明確な依存関係があります。 左半分に4つの開始点が表示されている場合、右半分がゼロの完了である場合は非常に驚くでしょう。 しかし、なぜ？..

隠されたスペース

各画像には1つの番号があります。 ログイン $$$\ mathbb {R} ^ {28×28}$ 明らかにこの情報は含まれていません。 しかし、それはどこかにあるに違いありません...この「どこか」は隠された空間です。







隠されたスペースは $$$\ mathbb {R} ^ {k}$ 各ベクトルには $$$k$ 画像のレンダリングに必要な情報。 最初の次元に数字で表される数値が含まれているとします。 2番目の次元は幅です。 3番目は角度などです。



2つのステップで人を描くプロセスを想像できます。 まず、人は-意識的か否か-表示される数字のすべての属性を決定します。 さらに、これらの決定は紙上のストロークに変換されます。



VAEはこのプロセスをシミュレートしようとしています：特定の画像 $$$x$ 私たちはそれを記述することができる少なくとも1つの隠れたベクトルを見つけたいです。 生成するための命令を含む1つのベクトル $$$x$ 。 総確率の式に従ってそれを定式化すると、 $$$P（x）= \ int P（x | z）P（z）dz$ 。



この方程式にいくつかの合理的な意味を入れましょう。

• インテグラルは、すべての隠された空間で候補者を探す必要があることを意味します。
• 各候補者について $$$z$ 私たちは質問をします：生成することは可能ですか？ $$$x$ 指示を使用して $$$z$ ？ 十分大きいですか $$$P（x | z）$ ？ たとえば、 $$$z$ 数字7に関する情報をエンコードすると、画像8は使用できません。 ただし、1と7は類似しているため、画像1は許容されます。
• 良いものを見つけました。 $$$z$ ？ いいね！ ちょっと待って...いくらですか $$$z$ たぶん？ $$$P（z）$ 十分な大きさ？ 反転した数字7の画像を考えてみましょう。理想的な一致は、ビュー7を説明する非表示のベクトルで、角度サイズは180°に設定されます。 しかし、そのような $$$z$ 通常、数字は180°の角度で書かれていないため、起こりそうにありません。

VAEトレーニングの目標は最大化することです $$$P（x）$ 。 モデリングします $$$P（x | z）$ 多次元ガウス分布を使用する $$$\ mathcal {N}（f（z）、\ sigma ^ 2 \ cdot I）$ 。



$$$f（z）$ ニューラルネットワークを使用してモデル化。 $$$\シグマ$ 単位行列を乗算するためのハイパーパラメーターです $$$I$ 。



覚えておいてください $$$f$ -これは、訓練されたモデルを使用して新しい画像を生成するために使用するものです。 ガウス分布の重複は、教育目的のみです。 ディラックのデルタ関数（つまり、決定論的 $$$x = f（z）$ ）、勾配降下を使用してモデルをトレーニングすることはできません！

隠された空間の驚異

隠しスペースのアプローチには、2つの大きな問題があります。

1. 各ディメンションにはどのような情報が含まれていますか？ 一部のディメンションは、スタイルなどの抽象要素に関連する場合があります。 すべてのディメンションを簡単に解釈できたとしても、データセットにラベルを割り当てたくありません。 このアプローチは、他のデータセットに拡張できません。
2. ディメンション間に相関がある場合、非表示スペースは混乱する可能性があります。 たとえば、非常に高速に描画された数字は、同時に角度のある細いストロークの出現につながります。 これらの依存関係を定義することは困難です。

ディープラーニングが助けになります

かなり複雑な関数を標準の多次元ガウス分布に適用することにより、各分布を生成できることがわかります。



選ぶ $$$P（z）$ 標準の多次元ガウス分布として。 したがって、ニューラルネットワークによってシミュレートされます $$$f$ 次の2つのフェーズに分けることができます。

1. 最初のレイヤーは、ガウス分布を隠し空間上の真の分布にマッピングします。 測定値を解釈することはできませんが、問題ではありません。
2. 隠されたスペースから次のレイヤーが表示されます $$$P（x | z）$ 。

それでは、この獣をどのように訓練するのでしょうか？

フォーミュラ $$$P（x）$ 不溶性なので、モンテカルロ法で近似します。

1. セレクション $$$\ {z_i \} _ {i = 1} ^ n$ 前から $$$P（z）$
2. との近似 $$$P（x）\約\ frac {1} {n} \ sum_ {i = 1} ^ n P（x | z_i）$

いいね！ いろいろ試してみてください $$$z$ バグ伝播パーティーを開始します！



残念ながら $$$x$ 非常に多次元で、合理的な近似を得るには、多くのサンプルが必要です。 やってみたら $$$z$ 、その後、次のような画像を取得する可能性は何ですか $$$x$ ？ ところで、これは理由を説明します $$$P（x | z）$ 可能な画像に正の確率値を割り当てる必要があります。そうしないと、モデルは学習できません。サンプリング $$$z$ ほぼ確実に異なる画像になります $$$x$ 、および確率が0の場合、勾配は伝播できません。



この問題を解決するには？

道を切り開いてください！

ほとんどのサンプル $$$z$ 選択範囲に何も追加されません $$$P（x）$ -彼らは国境を越えすぎています。 さて、あなたがそれらをどこから入手するかを事前に知っていれば...



入ることができます $$$Q（z | x）$ 。 与えられた $$$Q$ 高い確率値を割り当てるように訓練されます $$$z$ 生成する可能性が高い $$$x$ 。 これで、モンテカルロ法を使用して評価を行うことができます。 $$$Q$ 。



残念ながら、新しい問題が発生します！ 最大化する代わりに $$$P（x）= \ int P（x | z）P（z）dz = \ mathbb {E} _ {z \ sim P（z）} P（x | z）$ 最大化する $$$\ mathbb {E} _ {z \ sim Q（z | x）} P（x | z）$ 。 それらは互いにどのように関係していますか？

変分結論

変分結論は別の記事のトピックであるため、ここでは詳しく説明しません。 これらの分布はこの方程式によって関係しているとしか言えません。

$$

$$log P（X）-\ mathcal {KL} [Q（z | x）|| P（z | x）] = \ mathbb {E} _ {z \ sim Q（z | x）} [log P（x | z）]-\ mathcal {KL} [Q（z | x）|| P（z）]$$

$$$\ mathcal {KL}$ Kullback – Leibler distanceであり、2つの分布の類似性を直感的に評価します。



すぐに、方程式の右側を最大化する方法がわかります。 この場合、左側も最大化されます。

• $$$P（x）$ 最大化。
• どこまで $$$Q（z | x）$ から $$$P（z | x）$ - 実際のアプリオリ不明-最小化されます。

方程式の右側の意味は、ここに緊張があるということです。

1. 一方では、どれだけうまく $$$x$ からデコードする必要があります $$$z \ sim Q$ 。
2. 一方、私たちは欲しい $$$Q（z | x）$ （ エンコーダー ）は以前のものと同様でした $$$P（z）$ （多次元ガウス分布）。 これは正則化と見なすことができます。

発散の最小化 $$$\ mathcal {KL}$ 適切なディストリビューションを選択して簡単に実行できます。 シミュレートします $$$Q（z | x）$ ニューラルネットワークとして、その出力は多次元ガウス分布のパラメーターです。

• 平均的 $$$\ mu_Q$
• 対角共分散行列 $$$\ Sigma_Q$

それから分岐 $$$\ mathcal {KL}$ 分析的に解けるようになり、これは私たちにとって（そして勾配にとって）素晴らしいことです。



デコーダー部分はもう少し複雑です。 一見、この問題はモンテカルロ法では解決できないと述べたいと思います。 しかし、サンプル $$$z$ から $$$Q$ グラデーションが伝播することを許可しません $$$Q$ 、選択は微分可能な操作ではないため。 これは問題です。なぜなら、層の重みが $$$\ Sigma_Q$ そして $$$\ mu_Q$ 。

新しいパラメーター化のトリック

交換できます $$$Q$ ノンパラメトリック確率変数の決定論的パラメーター化変換：

1. 標準（パラメーターなし）ガウス分布からのサンプル。
2. サンプルに平方根を掛ける $$$\ Sigma_Q$ 。
3. 結果への補遺 $$$\ mu_Q$ 。

その結果、次の分布になります。 $$$Q$ 。 フェッチ操作は、標準のガウス分布から行われます。 その結果、勾配は $$$\ Sigma_Q$ そして $$$\ mu_Q$ 現在、これらは決定的なパスです。



結果？ モデルはパラメーターの調整方法を学習できます $$$Q$ ：彼女は良いことに集中します $$$z$ 生産できる $$$x$ 。

すべてをまとめる

VAEモデルを理解するのは難しい場合があります。 ここでは、消化するのが難しい多くの資料を検討しました。



VAEを実装するためのすべての手順を要約します。







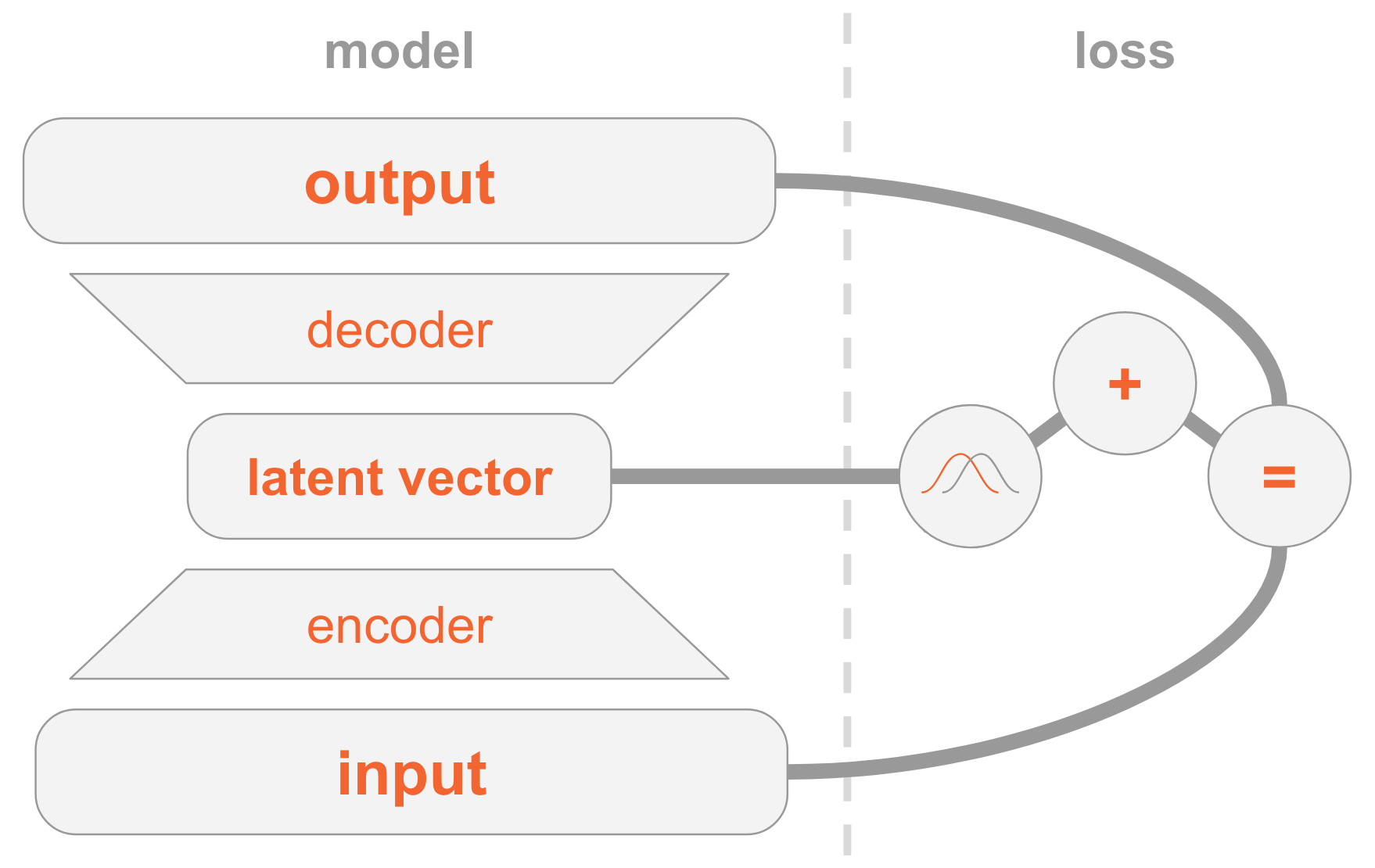
左側にモデル定義があります：

1. 入力画像はエンコーダネットワークを介して送信されます。
2. エンコーダーは分布パラメーターを提供します $$$Q（z | x）$ 。
3. 非表示のベクトル $$$z$ から取られた $$$Q（z | x）$ 。 エンコーダーが十分に訓練されている場合、ほとんどの場合 $$$z$ 説明を含む $$$x$ 。
4. デコーダーデコード $$$z$ 画像に。

右側には、損失関数があります。

1. 回復エラー：出力は入力に類似している必要があります。
2. $$$Q（z | x）$ 前のもの、つまり、多次元標準正規分布に似ている必要があります。

新しい画像を作成するには、以前の分布から非表示のベクトルを直接選択し、それを画像にデコードします。

作業コード

ここで、VAEをより詳細に研究し、作業コードを検討します。 VAEの実装に必要なすべての技術的詳細を理解できます。 おまけとして、興味深いトリックを紹介します。モデルが指定された数値の画像の生成を開始できるように、隠しベクトルのいくつかの次元に特別な役割を割り当てる方法です。

import numpy as np import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt np.random.seed(42) tf.set_random_seed(42) %matplotlib inline
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

モデルは手書きの数字のセットであるMNISTでトレーニングされていることを思い出させてください。 入力画像は次の形式です $$$\ mathbb {R} ^ {28×28}$ 。

 mnist = input_data.read_data_sets('MNIST_data') input_size = 28 * 28 num_digits = 10
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、ハイパーパラメーターを定義します。



さまざまな値を自由に試して、それらがモデルにどのように影響するかを理解してください。

 params = { 'encoder_layers': [128], #       'decoder_layers': [128], #    (CNN ,     ) 'digit_classification_layers': [128], #   ,   'activation': tf.nn.sigmoid, #      'decoder_std': 0.5, #   P(x|z)   'z_dim': 10, #    'digit_classification_weight': 10.0, #   ,   'epochs': 20, 'batch_size': 100, 'learning_rate': 0.001 }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

モデル

モデルは3つのサブネットで構成されます。

1. 取得 $$$x$ （イメージ）、それをディストリビューションにエンコードします $$$Q（z | x）$ 隠された空間で。
2. 取得 $$$z$ 隠されたスペース（画像のコード表現）で、対応する画像にデコードします $$$f（z）$ 。
3. 取得 $$$x$ また、10次元のレイヤーと比較して数値を決定します。i番目の値にはi番目の数値の確率が含まれます。

最初の2つのサブネットは、純粋なVAEの基盤です。



3番目は、非表示の次元の一部を使用して、画像内で見つかった数値をエンコードする補助タスクです。 その理由を説明します。先ほど、隠された空間の各次元にどんな情報が含まれているかは気にしないと話しました。 モデルは、タスクに役立つと考えられる情報をコーディングする方法を学習できます。 データセットに精通しているため、ディジットのタイプ（つまり、数値）を含むディメンションの重要性を知っています。 そして今、私たちは彼女にこの情報を提供することでモデルを助けたいと思っています。



特定のタイプの数字については、直接エンコードします。つまり、サイズ10のベクトルを使用します。これらの10個の数字は隠しベクトルに関連付けられています。



直接コーディングベクトルモデルを提供するには、2つの方法があります。

1. 入力をモデルに追加します。
2. モデル自体が予測を計算できるように、ラベルとして追加します。10次元ベクトルを予測する別のサブネットを追加します。ここで、損失関数は予想されるフォワードコーディングベクトルとのクロスエントロピーです。

2番目のオプションを選択します。 なんで？ それでは、テストするときに、モデルを2つの方法で使用できます。

1. 入力として画像を指定し、非表示のベクトルを表示します。
2. 入力として非表示のベクトルを指定し、画像を生成します。

最初のオプションをサポートしたいので、テスト中にそれを知りたくないので、モデルに入力として数字を与えることはできません。 したがって、モデルは予測を学習する必要があります。

 def encoder(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) mu = tf.layers.dense(x, params['z_dim']) var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim'])) return mu, var def decoder(z, layers): for layer in layers: z = tf.layers.dense(z, layer, activation=params['activation']) mu = tf.layers.dense(z, input_size) return tf.nn.sigmoid(mu) def digit_classifier(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) logits = tf.layers.dense(x, num_digits) return logits
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 images = tf.placeholder(tf.float32, [None, input_size]) digits = tf.placeholder(tf.int32, [None]) #        encoder_mu, encoder_var = encoder(images, params['encoder_layers']) #     ,  #     eps = tf.random_normal(shape=[tf.shape(images)[0], params['z_dim']], mean=0.0, stddev=1.0) z = encoder_mu + tf.sqrt(encoder_var) * eps # classify the digit digit_logits = digit_classifier(images, params['digit_classification_layers']) digit_prob = tf.nn.softmax(digit_logits) #     ,  #    decoded_images = decoder(tf.concat([z, digit_prob], axis=1), params['decoder_layers'])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 #    ,    #    loss_reconstruction = -tf.reduce_sum( tf.contrib.distributions.Normal( decoded_images, params['decoder_std'] ).log_prob(images), axis=1 ) #         . #      , #         #  ,  KL-   # ,    loss_prior = -0.5 * tf.reduce_sum( 1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var, axis=1 ) loss_auto_encode = tf.reduce_mean( loss_reconstruction + loss_prior, axis=0 ) # digit_classification_weight      , #      loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits, logits=digit_logits), axis=0 ) loss = loss_auto_encode + loss_digit_classifier train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

トレーニング

SGDを使用して、2つの損失関数（VAEと分類）を最適化するモデルをトレーニングします 。



各エポックの終わりに、非表示のベクトルを選択して画像にデコードし、モデルの生成力がエポックを超えてどのように改善されるかを視覚的に観察します。 サンプリング方法は次のとおりです。

1. 生成する数字で分類するために使用されるディメンションを明示的に設定します。 たとえば、数値2の画像を作成する場合は、測定値を設定します $$$[0010000000]$ 。
2. 多次元正規分布の他の次元からランダムに選択します。 これらは、この時代に生成されるさまざまな数値の値です。 これにより、手書きスタイルなど、他の次元でエンコードされるものがわかります。

ステップ1の意味は、収束後、モデルがこれらの測定設定によって入力画像内の図を分類できることです。 ただし、これらはイメージを作成するためのデコードフェーズでも使用されます。 つまり、デコーダーのサブネットは次のことを認識しています。測定値が図2に対応する場合、この図で画像を生成する必要があります。 したがって、測定値を手動で2に設定すると、この図の生成された画像が得られます。

 samples = [] losses_auto_encode = [] losses_digit_classifier = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for epoch in xrange(params['epochs']): for _ in xrange(mnist.train.num_examples / params['batch_size']): batch_images, batch_digits = mnist.train.next_batch(params['batch_size']) sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits}) train_loss_auto_encode, train_loss_digit_classifier = sess.run( [loss_auto_encode, loss_digit_classifier], {images: mnist.train.images, digits: mnist.train.labels}) losses_auto_encode.append(train_loss_auto_encode) losses_digit_classifier.append(train_loss_digit_classifier) sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1]) gen_samples = sess.run(decoded_images, feed_dict={z: sample_z, digit_prob: np.eye(num_digits)}) samples.append(gen_samples)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

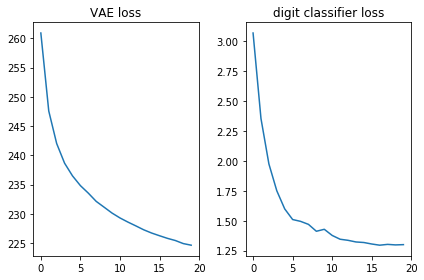
両方の損失関数が適切に見えること、つまり減少することを確認しましょう：

 plt.subplot(121) plt.plot(losses_auto_encode) plt.title('VAE loss') plt.subplot(122) plt.plot(losses_digit_classifier) plt.title('digit classifier loss') plt.tight_layout()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

さらに、生成された画像を表示し、モデルが実際に手書きの数字で写真を作成できるかどうかを確認しましょう。

 def plot_samples(samples): IMAGE_WIDTH = 0.7 plt.figure(figsize=(IMAGE_WIDTH * num_digits, len(samples) * IMAGE_WIDTH)) for epoch, images in enumerate(samples): for digit, image in enumerate(images): plt.subplot(len(samples), num_digits, epoch * num_digits + digit + 1) plt.imshow(image.reshape((28, 28)), cmap='Greys_r') plt.gca().xaxis.set_visible(False) if digit == 0: plt.gca().yaxis.set_ticks([]) plt.ylabel('epoch {}'.format(epoch + 1), verticalalignment='center', horizontalalignment='right', rotation=0, fontsize=14) else: plt.gca().yaxis.set_visible(False) plot_samples(samples)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

おわりに

単純な直接配信ネットワーク（派手な畳み込みなし）がわずか20時代の美しい画像を生成するのを見るのは素晴らしいことです。 モデルは、数値に特別な測定値を使用することをすぐに学びました。第9の時代には、生成しようとしていた数値のシーケンスが既に表示されています。



各エポックは他の次元に異なるランダム値を使用したため、時代によってスタイルは異なりますが、それらの内部では少なくとも一部の内部で似ています。 たとえば、18日では、すべての数値が20日と比較して太くなっています。

注釈

この記事は、私の経験と次のソースに基づいています。

• 変分的結論と深層学習：新しい統合
• バリエーションオートコーダーガイド