2016年3月、スタンフォード大学のRobert J. Lemke-OliverとKannan Sundararajanは素数の分布に新しいパターンを開きました 。 素数は、数値空間に明確に分布していることが判明しました。 詳細については、Habréの記事「素数の構造とランダム性」の翻訳を参照してください。
化学を含む他の分野の専門家がこのトピックの研究に参加しました。 そして成功しました。 数理理論家のマシュー・ド・クールシー・アイルランドとともに、理論化学のサルバトーレ・トルクアト教授は、これまで知られていなかった素数の分布に新しいパターンを発見しました。 素数の分布は、エキゾチックな準結晶の回折パターンにいくらか似たフラクタルのような回折パターンを形成することが判明しました。
Torcuato教授は、結晶やコロイドなどの物理システムの構造のパターンの研究を専門としています。 構造を研究する標準的な方法は、X線回折です。 液体または気体中のランダム分子は、目立ったパターンを作成することなく、あらゆる方向の光線を反射します。 しかし、結晶内の対称的に配置された原子は、光波を同期的に反射し、顕著な回折の周期的な明るいスポット( ブラッグピーク )を作成します。 ブラッグピークの分析により、そのような写真を作成する結晶またはその他の材料の内部構造を理解することができます。
そのため、Torkuatoらによる新しい科学論文( 1、2、3 )では、素数の分布で発見された秩序構造は、準結晶のそれに類似したフラクタルのような回折パターンに過ぎないことが示されています。
素数の格子上のブラッグピークの図は準結晶に似ていますが、まだ異なっています。 Torcuato は 、物理システムとしての素数は「構造のまったく新しいカテゴリである」 と言います。 研究者は、この新しいフラクタルのようなパターンを「効果的な限界周期性」と呼んでいます。
この図は、最も一般的な素数間隔を反映する周期的な明るいピークのシーケンスで構成されています。それらはすべて奇数(2を除く)で、多くが隣り合っています。 最も明るいピーク(2桁で区切られたペア)は、6桁で区切られた素数を反映して、一定の間隔で交互に明るくなります。 それらの間には、より遠くの素数のペアなどに対応するかすかなピークもあります。これはすべて、互いに内に配置された無限の数のブラッグピークです。
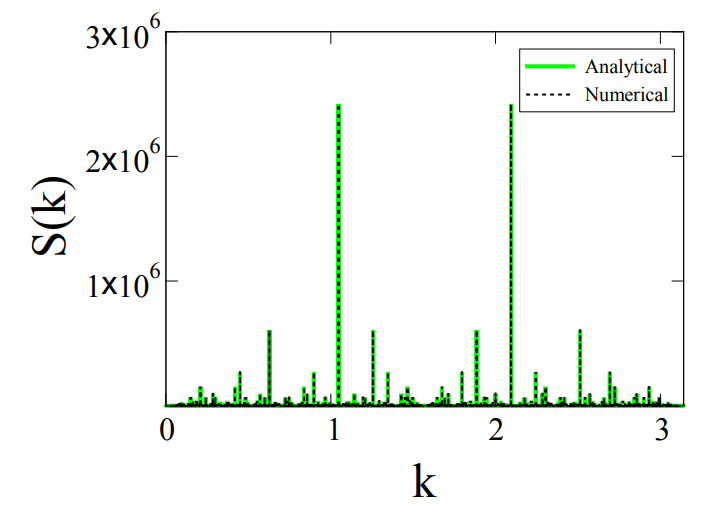
準結晶の回折パターンで、ブラッグピークの同様の構造が以前に観察されました。
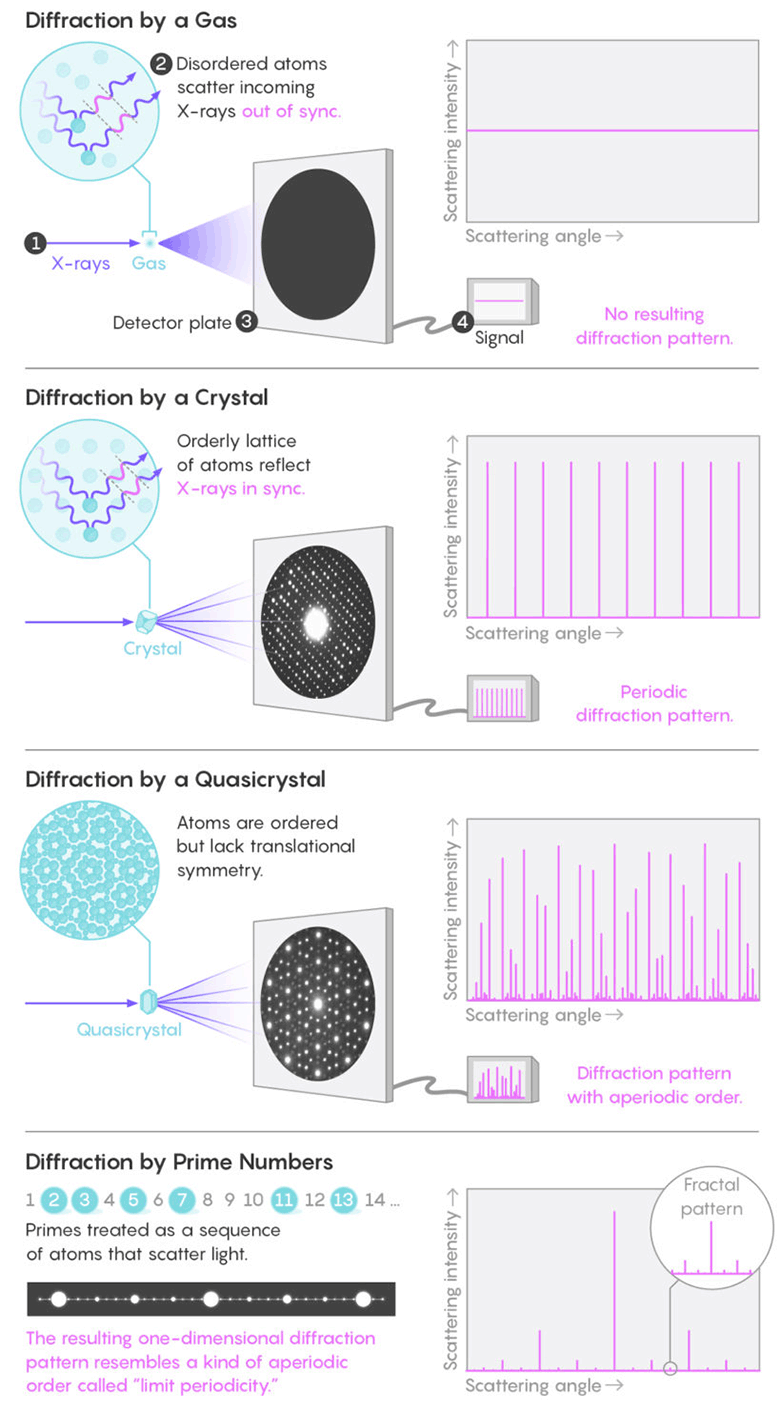
液体または気体中のランダム分子は、目立ったパターンを作成することなく、あらゆる方向の光線を反射します。 しかし、結晶内の対称的に配置された原子は光波を同期的に反射し、顕著な回折の周期的な明るいスポットを作成します。 判明したように、素数の分布パターンは、準結晶の分布パターンに似たフラクタル回折パターンを形成します
準結晶は、1980年代に発見された奇妙な物質です。 それらは、古典的な結晶学で禁じられている対称性と長距離秩序の存在によって特徴付けられます。 有名なペンローズモザイクのタイプの非周期的モザイクは、準結晶の数学モデルです。 このようなモザイクには並進対称性はなく、再現性と準結晶化度(5次対称性)があります。
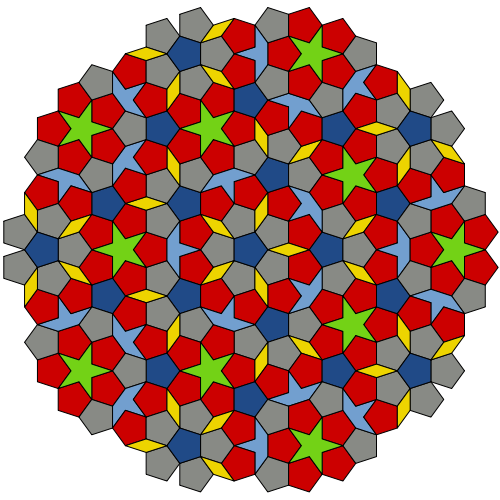
ペンローズモザイクタイプP1のフラグメント(6種類のタイルから)
素数の場合、準結晶の不合理な間隔のブラッグピークとは対照的に、ピーク間の距離は互いに比例します。 「実際の素数は、準結晶と似ていますが、準結晶とは異なり、粒子位置の完全に異なる状態を意味します」 とトルカトは言いました。
回折パターンの発見は、数論の画期的な発見とは言えません。これらのパターンの主要部分は、すでに準結晶の回折ではなく、他の数学的方法によってのみ既に説明されているためです。 したがって、回折パターンを使用すると、タイプ17および19の「ダブル」を予測することができます。これは、数直線の特定のセグメント上の素数のタプルの存在に関する最初のHardy-Littlewood仮説と数学的に同等です。 ルールの1つは、{3、5、7}の後の連続する奇数のトリプレットを禁止しています。 これは、回折パターンで次に明るいブラッグピークが4ではなく6桁で区切られた数値に対応する理由も説明します。
新しい科学的研究は、素数の均一な分布の問題を新たに見たものであり、素数のための特定の「単一の法則」を導き出すより簡単な方法です。 さらに、これは、結晶学の観点から、つまり非反復モデルを研究し、結晶学、力学系、調和解析、離散幾何学の交点にある「非周期的秩序」と呼ばれる比較的若い研究分野の観点から数学的な問題を分析する珍しい方法です。 この科学分野は、準結晶が発見されてから成長し、古い方法がここでは機能しないことが明らかになりました。
素数の分布は、1950年代から知られている特別な非周期的秩序に似ています。 これは限界周期性と呼ばれます。 このようなシステムでは、周期的な間隔が無限階層にネストされるため、任意の間隔で、システムには、Taylor-Sokolarタイルのように、より大きな間隔でのみ繰り返されるパターンの一部が含まれます。

Taylor-Sokolarタイル
理論計算では、物質の最大周期相は自然に形成できるはずであり、そのようなシステムには異常な特性がある可能性があります。 しかし、限られた周期性を素数に結びつけるとは誰も思いませんでした。 このような関係があり、プライムは新しい種類の制限周期性を示します。システム全体のプライム間の距離の同期は統計的にのみ観察されるため、「効果的な」制限周期性です。
問題が発生します。素数の分布のパターンは、暗号アルゴリズムの強度にどのように影響しますか?
「このテーマについて本当にたくさんの手紙をもらいました。 これは興味深い研究ですが、暗号学とは何の関係もありません、有名な暗号学者ブルース・シュナイアーは彼のブログに書いています。 -暗号作成者は、素数やその分布を見つけることに興味がありません。 RSAタイプの公開キー暗号化アルゴリズムの強さは、素数の積である大きな合成数を因数分解することの困難さに関連しています。 これはまったく別の問題です。」
そのため、素数の分布の研究が進歩しているにもかかわらず、暗号コードの強度を心配する必要はまだありません。
