
私たちの「与えられた:」
したがって、計算タスクの本質は、非ブロッキング遅延ポイントツーポイント送信を使用するプログラムが、ブロッキングポイントツーポイント送信を使用するプログラムよりも高速である回数を比較することです。 寸法64、256、1024、4096、8192、16384、65536、262144、1048576、4194304、16777216、335554432要素の入力配列に対して測定が実行されます。 デフォルトでは、4つのプロセスで解決することが提案されています。 そして、実際に、ここで我々が検討するものです:
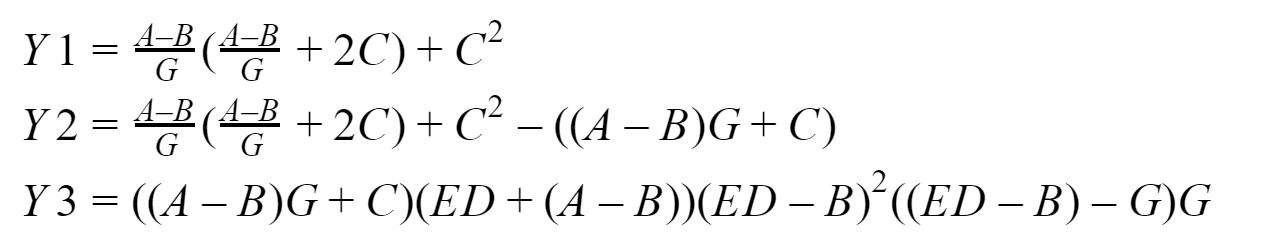
出力では、ゼロプロセスが収集する3つのベクトル、Y1、Y2、Y3を取得する必要があります。 16 GBのRAMを搭載したIntelプロセッサをベースにしたシステムで、このすべてをテストします。 プログラムを開発するには、Fortranではなく、Visual Studio Community 2017のMicrosoftバージョン9.0.1 (執筆時点では関連しています)のMPI標準の実装を使用します 。
マテリエル
使用されるMPI関数がどのように機能するかを詳細に説明したくありません。いつでもこのドキュメントを参照できますので、使用するものの概要のみを説明します。
ブロッキング交換
ポイントツーポイントメッセージングをブロックするには、次の関数を使用します。
MPI_Send-メッセージ送信のブロックを実装します。 関数を呼び出した後、プロセスは、送信されたデータがメモリからMPI内部システムバッファに書き込まれるまでブロックされます。その後、プロセスはさらに動作し続けます。
MPI_Recv-メッセージ受信のブロックを実行します。 関数を呼び出した後、送信プロセスからのデータが到着し、このデータがMPI環境によって受信プロセスのバッファに完全に書き込まれるまで、プロセスはブロックされます。
遅延なしの非交換交換
遅延ノンブロッキングポイントツーポイントメッセージングの場合、次の関数を使用します。
MPI_Send_init-バックグラウンドで、将来的にロックが発生しないデータを送信するための環境を準備します。
MPI_Recv_init-この関数は前の関数と同様に機能しますが、今回はデータを受信します。
MPI_Start-メッセージを受信または送信するプロセスを開始します。これはa.k.aのバックグラウンドでも実行されます。 ブロッキングなし;
MPI_Wait-メッセージの送信または受信の完了を確認し、必要に応じて待機しますが、必要に応じてプロセスをブロックするだけです(データが「送信されない」または「受信されない」場合)。 たとえば、プロセスはまだ到達していないデータを使用したい-良くないため、このデータが必要な場所の前にMPI_Waitを挿入します(単にデータ破損のリスクがある場合でも挿入します)。 別の例として、プロセスはバックグラウンドデータ転送を開始し、データ転送を開始した後、すぐに何らかの形でこのデータを変更し始めました-良くないので、このデータを変更し始めるプログラムの場所の前にMPI_Waitを挿入します(ここでも、単にデータ破損のリスクがあります)。
したがって、 意味的には 、遅延なしの非交換交換による呼び出しのシーケンスは次のとおりです。
- MPI_Send_init / MPI_Recv_init-受信または送信のための環境を準備する
- MPI_Start-受信/送信のプロセスを開始します
- MPI_Wait-送信または受信されたデータの損傷のリスク(「アンダーセンディング」および「アンダーレポート」を含む)
また、テストプログラムでMPI_Startall 、 MPI_Waitallを使用しました 。それらの意味は基本的にそれぞれMPI_StartおよびMPI_Waitと同じであり、複数のパッケージおよび/またはトランスミッションでのみ動作します。 ただし、これは開始および待機関数のリスト全体ではなく、操作の完全性をチェックするための関数がいくつかあります。
プロセス間通信アーキテクチャ
明確にするために、4つのプロセスで計算を実行するためのグラフを作成します。 この場合、すべてのベクトル算術演算をプロセス全体に比較的均等に分散させる必要があります。 ここに私が得たものがあります:
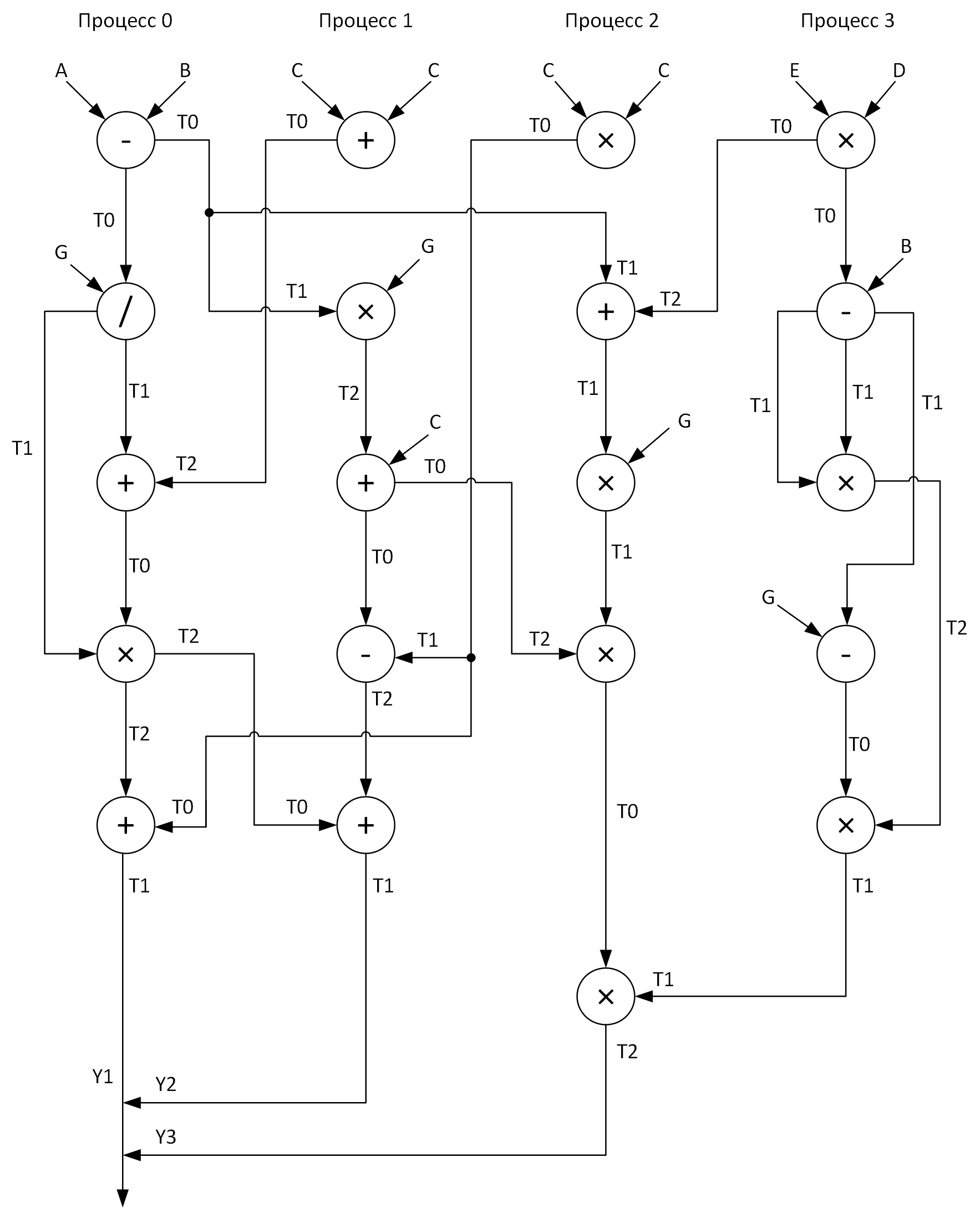
これらのアレイT0-T2を参照してください? これらは、操作の中間結果を保存するためのバッファーです。 また、あるプロセスから別のプロセスにメッセージを送信するときのグラフでは、矢印の先頭にデータが送信されるアレイの名前があり、矢印の末尾にこのデータを受信するアレイがあります。
それで、ついに質問に答えたとき:
- どのような問題を解決していますか?
- それを解決するためにどのような意味がありますか?
- どのように解決しますか?
それを解決するためだけに残っています...
「ソリューション:」
次に、上で説明した2つのプログラムのコードを紹介しますが、まずは何をどのように説明するかをもう少し説明します。
コードの読みやすさを向上させるために、すべてのベクトル算術演算を個別の手順(add、sub、mul、div)で取り出しました。 すべての入力配列は、 ほぼランダムに指定した式に従って初期化されます。 ゼロプロセスは他のすべてのプロセスから作業結果を収集するため、最も長く機能します。したがって、最初と2番目のケースでは、作業時間をプログラムの実行時間に等しいと考えるのが論理的です(覚えているとおり、算術+メッセージング)。 MPI_Wtime関数を使用して時間間隔を測定し、同時にMPI_Wtickを使用してそこにある時計の解像度を表示することにしました (私の魂のどこかで、不変のTSCに適合することを望みます。 MPI_Wtime関数が呼び出された時刻に関連付けられています)。 それで、私が上で書いたすべてをまとめ、グラフに従って最終的にこれらのプログラムを開発します(そしてもちろんデバッグもします)。
コードを見たい人:
データ転送をブロックするプログラム
#include "pch.h" #include <iostream> #include <iomanip> #include <fstream> #include <mpi.h> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main(int argc, char **argv) { if (argc < 2) { return 1; } int n = atoi(argv[1]); int rank; double start_time, end_time; MPI_Status status; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; double *D = new double[n]; double *E = new double[n]; double *G = new double[n]; double *T0 = new double[n]; double *T1 = new double[n]; double *T2 = new double[n]; for (int i = 0; i < n; i++) { A[i] = double (2 * i + 1); B[i] = double(2 * i); C[i] = double(0.003 * (i + 1)); D[i] = A[i] * 0.001; E[i] = B[i]; G[i] = C[i]; } cout.setf(ios::fixed); cout << fixed << setprecision(9); MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &rank); if (rank == 0) { start_time = MPI_Wtime(); sub(A, B, T0, n); MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); div(T0, G, T1, n); MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); add(T1, T2, T0, n); mul(T0, T1, T2, n); MPI_Recv(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); MPI_Send(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); add(T0, T2, T1, n); MPI_Recv(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); MPI_Recv(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); end_time = MPI_Wtime(); cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl; cout << "Thread " << rank << " execution time: " << end_time - start_time << endl; } if (rank == 1) { add(C, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); mul(T1, G, T2, n); add(T2, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); sub(T1, T0, T2, n); MPI_Recv(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); add(T0, T2, T1, n); MPI_Send(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); } if (rank == 2) { mul(C, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); MPI_Recv(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); add(T1, T2, T0, n); mul(T0, G, T1, n); MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); mul(T1, T2, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status); mul(T0, T1, T2, n); MPI_Send(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); } if (rank == 3) { mul(E, D, T0, n); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); sub(T0, B, T1, n); mul(T1, T1, T2, n); sub(T1, G, T0, n); mul(T0, T2, T1, n); MPI_Send(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); } MPI_Finalize(); delete[] A; delete[] B; delete[] C; delete[] D; delete[] E; delete[] G; delete[] T0; delete[] T1; delete[] T2; return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
遅延なしの非ブロッキングデータ転送を使用するプログラム
#include "pch.h" #include <iostream> #include <iomanip> #include <fstream> #include <mpi.h> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main(int argc, char **argv) { if (argc < 2) { return 1; } int n = atoi(argv[1]); int rank; double start_time, end_time; MPI_Request request[7]; MPI_Status statuses[4]; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; double *D = new double[n]; double *E = new double[n]; double *G = new double[n]; double *T0 = new double[n]; double *T1 = new double[n]; double *T2 = new double[n]; for (int i = 0; i < n; i++) { A[i] = double(2 * i + 1); B[i] = double(2 * i); C[i] = double(0.003 * (i + 1)); D[i] = A[i] * 0.001; E[i] = B[i]; G[i] = C[i]; } cout.setf(ios::fixed); cout << fixed << setprecision(9); MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &rank); if (rank == 0) { start_time = MPI_Wtime(); MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[0]);// MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);// MPI_Send_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[5]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[6]);// MPI_Start(&request[2]); sub(A, B, T0, n); MPI_Startall(2, &request[0]); div(T0, G, T1, n); MPI_Waitall(3, &request[0], statuses); add(T1, T2, T0, n); mul(T0, T1, T2, n); MPI_Startall(2, &request[3]); MPI_Wait(&request[3], &statuses[0]); add(T0, T2, T1, n); MPI_Startall(2, &request[5]); MPI_Wait(&request[4], &statuses[0]); MPI_Waitall(2, &request[5], statuses); end_time = MPI_Wtime(); cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl; cout << "Thread " << rank << " execution time: " << end_time - start_time << endl; } if (rank == 1) { MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);// MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[1]);// MPI_Recv_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[2]);// MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[4]);// MPI_Send_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[5]);// MPI_Start(&request[0]); add(C, C, T0, n); MPI_Start(&request[1]); MPI_Wait(&request[0], &statuses[0]); mul(T1, G, T2, n); MPI_Start(&request[2]); MPI_Wait(&request[1], &statuses[0]); add(T2, C, T0, n); MPI_Start(&request[3]); MPI_Wait(&request[2], &statuses[0]); sub(T1, T0, T2, n); MPI_Wait(&request[3], &statuses[0]); MPI_Start(&request[4]); MPI_Wait(&request[4], &statuses[0]); add(T0, T2, T1, n); MPI_Start(&request[5]); MPI_Wait(&request[5], &statuses[0]); } if (rank == 2) { MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[1]);// MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);// MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[3]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);// MPI_Recv_init(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[5]);// MPI_Send_init(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[6]);// MPI_Startall(2, &request[0]); mul(C, C, T0, n); MPI_Startall(2, &request[2]); MPI_Waitall(4, &request[0], statuses); add(T1, T2, T0, n); MPI_Start(&request[4]); mul(T0, G, T1, n); MPI_Wait(&request[4], &statuses[0]); mul(T1, T2, T0, n); MPI_Start(&request[5]); MPI_Wait(&request[5], &statuses[0]); mul(T0, T1, T2, n); MPI_Start(&request[6]); MPI_Wait(&request[6], &statuses[0]); } if (rank == 3) { MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[0]); MPI_Send_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]); mul(E, D, T0, n); MPI_Start(&request[0]); sub(T0, B, T1, n); mul(T1, T1, T2, n); MPI_Wait(&request[0], &statuses[0]); sub(T1, G, T0, n); mul(T0, T2, T1, n); MPI_Start(&request[1]); MPI_Wait(&request[1], &statuses[0]); } MPI_Finalize(); delete[] A; delete[] B; delete[] C; delete[] D; delete[] E; delete[] G; delete[] T0; delete[] T1; delete[] T2; return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
テストと分析
さまざまなサイズの配列に対してプログラムを実行し、その結果を見てみましょう。 テスト結果を表にまとめ、最後の列で加速係数を計算して記述します。加速係数は次のように定義します。K accele = T ex。 非ブロック。 / T ブロック。
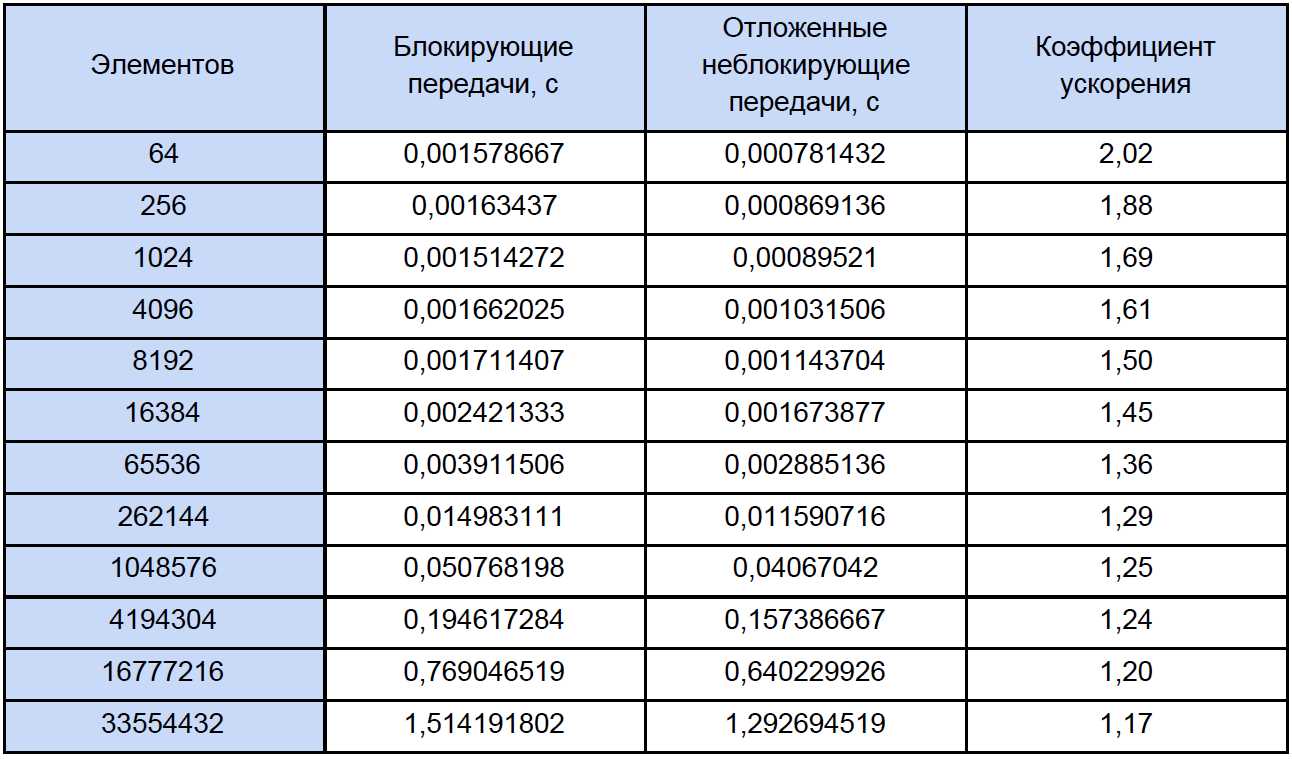
この表を通常よりも少し注意深く見ると、処理される要素の数が増えると、加速係数が次のように減少することがわかります。

何が問題なのか判断してみましょうか? これを行うには、各ベクトル算術演算の時間を測定し、結果を通常のテキストファイルに慎重に縮小する小さなテストプログラムを作成することを提案します。
ここで、実際には、プログラム自体:
時間測定
#include "pch.h" #include <iostream> #include <iomanip> #include <Windows.h> #include <fstream> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main() { struct res { double add; double sub; double mul; double div; }; int i, j, k, n, loop; LARGE_INTEGER start_time, end_time, freq; ofstream fout("test_measuring.txt"); int N[12] = { 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 }; SetConsoleOutputCP(1251); cout << " loop: "; cin >> loop; fout << setiosflags(ios::fixed) << setiosflags(ios::right) << setprecision(9); fout << " : " << loop << endl; fout << setw(10) << "\n " << setw(30) << ". (c)" << setw(30) << ". (c)" << setw(30) << ". (c)" << setw(30) << ". (c)" << endl; QueryPerformanceFrequency(&freq); cout << "\n : " << freq.QuadPart << " " << endl; for (k = 0; k < sizeof(N) / sizeof(int); k++) { res output = {}; n = N[k]; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; for (i = 0; i < n; i++) { A[i] = 2.0 * i; B[i] = 2.0 * i + 1; C[i] = 0; } for (j = 0; j < loop; j++) { QueryPerformanceCounter(&start_time); add(A, B, C, n); QueryPerformanceCounter(&end_time); output.add += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); sub(A, B, C, n); QueryPerformanceCounter(&end_time); output.sub += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); mul(A, B, C, n); QueryPerformanceCounter(&end_time); output.mul += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); div(A, B, C, n); QueryPerformanceCounter(&end_time); output.div += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); } fout << setw(10) << n << setw(30) << output.add / loop << setw(30) << output.sub / loop << setw(30) << output.mul / loop << setw(30) << output.div / loop << endl; delete[] A; delete[] B; delete[] C; } fout.close(); cout << endl; system("pause"); return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
起動時に、測定サイクルの数を入力するように求められます。10,000サイクルでテストしました。 出力では、各操作の平均結果を取得します。
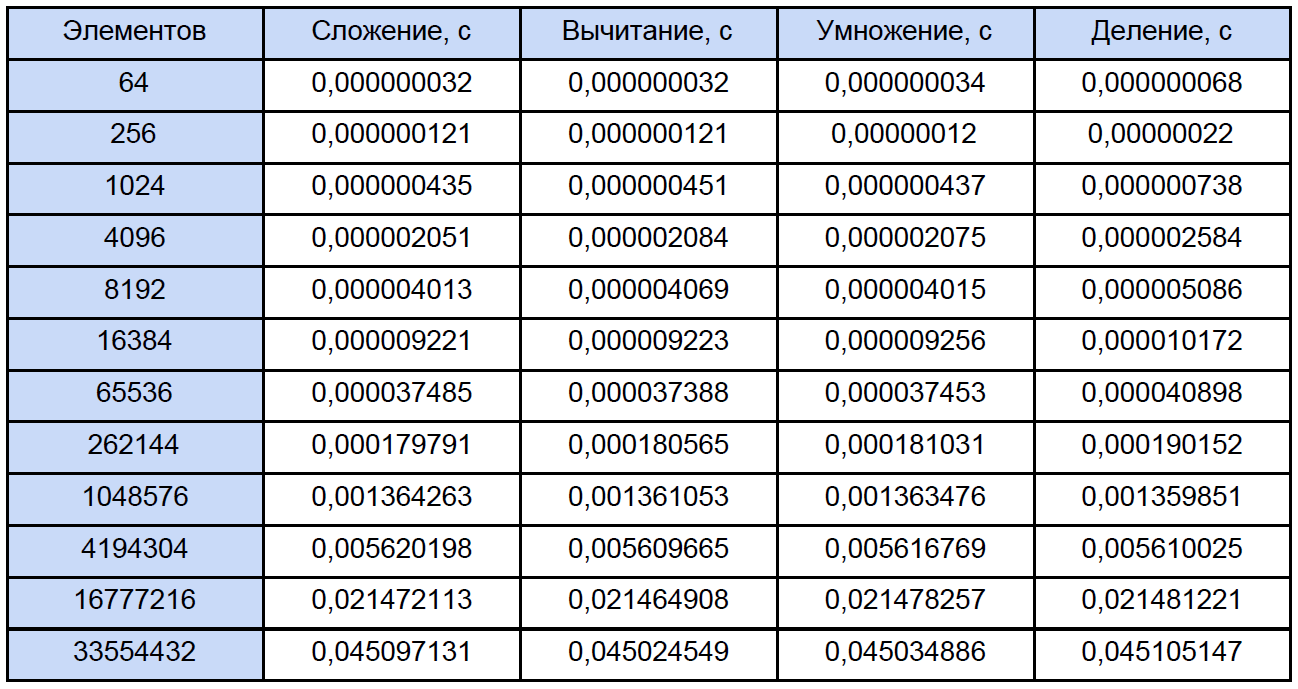
時間を測定するために、高レベルのQueryPerformanceCounterを使用しました。 このFAQを読むことを強くお勧めします。これにより、この機能を使用した時間の測定に関するほとんどの質問が自動的に消えます。 私の観察によれば、それはTSCにしがみついています(しかし、理論的にはそうではないかもしれません)が、助けによれば、カウンターの現在のティック数を返します。 しかし、実際には、私のカウンターは物理的に32 nsの時間間隔を測定できません(結果テーブルの最初の行を参照)。 この結果は、QueryPerformanceCounterの2つの呼び出し間で、0ティックまたは1ティックが通過するという事実によるものです。テーブルの最初の行については、10,000の結果の約3分の1が1ティックに等しいと結論付けることができます。 したがって、64、256、さらには1024要素の場合でも、この表のデータはかなり近似したものです。 それでは、プログラムを開いて、各タイプの合計操作数を計算してみましょう。伝統的に、次の表に従ってすべてを「拡散」します。
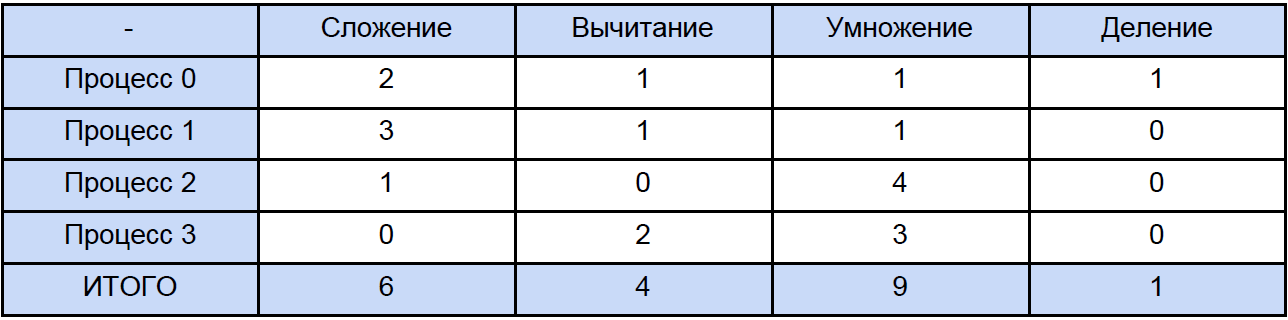
最後に、各ベクトル算術演算の時間とプログラム内の時間を把握し、並列プログラムでこれらの演算に費やされる時間と、プロセス間のブロックおよび遅延非ブロッキングデータ交換に費やされる時間を調べて、明確にするためにこれを減らします表:
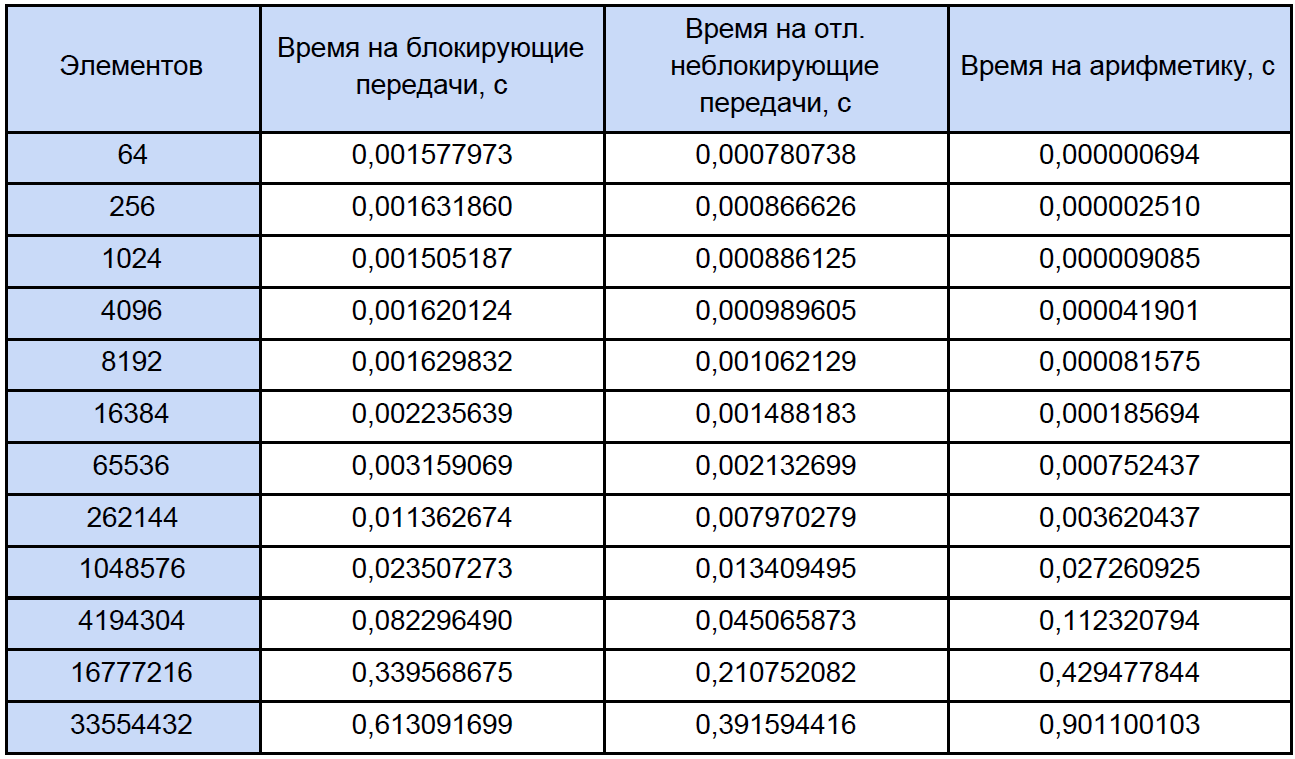
取得したデータの結果に基づいて、3つの関数のグラフを作成します:最初はプロセス間の転送のブロックに費やされた時間の変化を配列要素の数から、2番目はプロセス間の非ブロック転送の遅延に費やされた時間の変化、配列要素の数を、3番目は時間の変化を記述します、配列の要素の数から、算術演算に費やした:
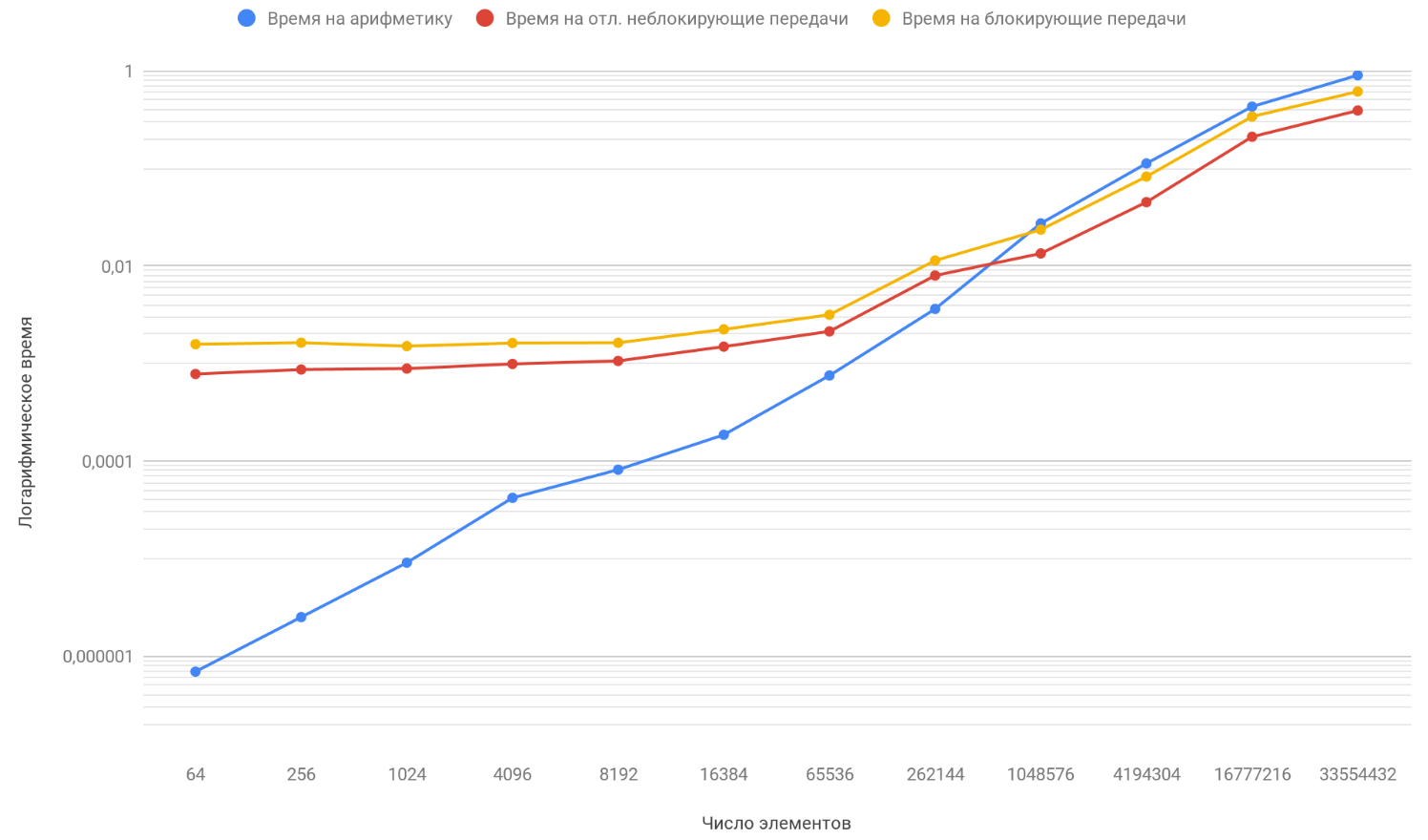
すでにお気付きのように、グラフの垂直スケールは対数であり、必要な尺度です。 時間のばらつきが大きすぎるため、通常のチャートでは何も表示されませんでした。 算術に費やされる時間の要素数への依存性の関数に注意してください;それは安全に他の2つの関数を約100万要素だけ上回っています。 問題は、2つの敵よりも無限に速く成長することです。 したがって、処理される要素の数が増えると、プログラムの実行時間は転送ではなく算術によってますます決定されます。 プロセス間の転送回数を増やしたと仮定すると、概念的には、算術関数が他の2つを追い越した瞬間が後で発生することしかわかりません。
まとめ
したがって、配列の長さを増やし続けると、遅延非ブロック転送を使用するプログラムは、ブロック交換を使用するプログラムよりもほんのわずかだけ高速になるという結論に達します。 そして、配列の長さを無限に向けると(まあ、または単に非常に長い配列を取る)、プログラムの動作時間は計算によって100%決定され、加速係数は安全に1になる傾向があります。