全方向シャドウマップ

前のレッスンでは、動的な投影シャドウを作成する方法を見つけました。 この手法はうまく機能しますが、残念なことに、シャドウマップは光源の方向に一致する1つの方向で作成されるため、指向性光源にのみ適しています。 これが、深度マップ（シャドウマップ）が光源の方向に正確に沿って作成されるため、この手法が方向シャドウマップとも呼ばれる理由です。



このレッスンは、あらゆる方向に投影する動的な影を作成することに専念します。 このアプローチは、スポットライトを一度にすべての方向に投影する必要があるため、スポットライトでの作業に最適です。 したがって、この手法は全方向シャドウマップと呼ばれます 。

このレッスンは、 前のレッスンの資料に大きく依存しているため、通常のシャドウマップを使用していない場合は、この記事の学習を続ける前にこれを行う必要があります。

一般に、操作アルゴリズムは有向影の場合とほぼ同じです。光源の視点から深度マップを作成し、各フラグメントについて深度の値を比較し、深度マップから読み取ります。 使用される深度マップのタイプにおける指向性アプローチと全方向性アプローチの主な違い。



必要なシャドウマップには、光源の周囲のすべての方向にシーンをレンダリングする必要があり、通常の2Dテクスチャはここでは良くありません。 だから多分立方マップを使用しますか？ 立方体マップは6つの面だけで環境データを保存できるため、これらの各面にシーン全体を描画し、立方体マップから深度を選択できます。









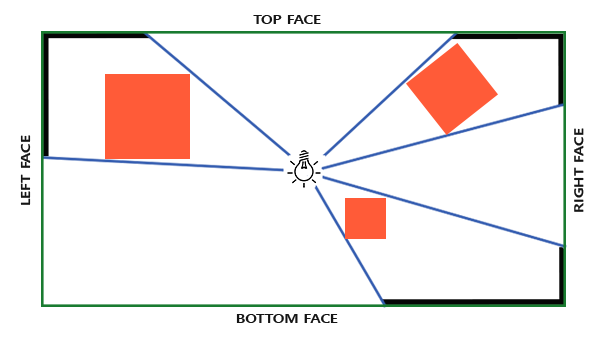
作成されたキュービックシャドウマップは、最終的にフラグメントシェーダーで終了し、方向ベクトルを使用してサンプリングされて、（ソースの視点から）フラグメント深度値を取得します。 前のレッスンで技術的に複雑な詳細のほとんどを既に説明したので、1つの微妙な点が残っています-3次マップを使用します。

立方体マップを作成する

光源の深度を格納する立方体マップを作成するには、マップの各面に1回ずつ、シーンを6回レンダリングする必要があります。 これを行う（明らかな）方法の1つは、6つの異なるビューマトリックスを使用してシーンを6回単純に描画し、各パスでキュービックマップの個別の面をフレームバッファーオブジェクトの色に接続することです。

for(unsigned int i = 0; i < 6; i++) { GLenum face = GL_TEXTURE_CUBE_MAP_POSITIVE_X + i; glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, face, depthCubemap, 0); BindViewMatrix(lightViewMatrices[i]); RenderScene(); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このアプローチは、単一のシャドウマップを作成するために多くの描画呼び出しが行われるため、パフォーマンスが非常に高くなります。 レッスンでは、幾何学的シェーダーの使用に関連する小さなトリックを使用して、より最適なアプローチを実装しようとします。 これにより、1回のパスでキュービック深度マップが作成されます。



最初に、キュービックマップを作成します。

 unsigned int depthCubemap; glGenTextures(1, &depthCubemap);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、各面を深さの値を保存する2Dテクスチャとして設定します。

 const unsigned int SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024; glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap); for (unsigned int i = 0; i < 6; ++i) glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_DEPTH_COMPONENT, SHADOW_WIDTH, SHADOW_HEIGHT, 0, GL_DEPTH_COMPONENT, GL_FLOAT, NULL);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また、適切なテクスチャパラメータを設定することを忘れないでください。

 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_NEAREST); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_NEAREST); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

通常のアプローチでは、キュービックマップの各面をフレームバッファーに接続し、各パスでシーンを6回レンダリングし、フレームバッファーの深度アタッチメントに接続されたキュービックマップの面を置き換えます。 ただし、ジオメトリシェーダーを使用すると、1回のパスで一度にすべての側面にシーンを持ち込むことができるため、立方体マップを深度アタッチメントに直接接続します。

 glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO); glFramebufferTexture(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, depthCubemap, 0); glDrawBuffer(GL_NONE); glReadBuffer(GL_NONE); glBindFramebuffer(GL_FRAMEBUFFER, 0);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

繰り返しになりますが、 glDrawBufferとglReadBufferの呼び出しに注意してください。深度の値のみが重要であるため、OpenGLにカラーバッファーに書き込むことができないことを明示的に伝えます。

最終的に、2つのパスがここに適用されます。最初にシャドウマップが準備され、次にシーンが描画され、マップを使用してシェーディングが作成されます。 フレームバッファーとキュービックマップを使用すると、コードは次のようになります。

 // 1.      glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT); glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO); glClear(GL_DEPTH_BUFFER_BIT); ConfigureShaderAndMatrices(); RenderScene(); glBindFramebuffer(GL_FRAMEBUFFER, 0); // 2.           glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT); glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); ConfigureShaderAndMatrices(); glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap); RenderScene();
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初の近似では、プロセスは方向シャドウマップを使用する場合と同じです。 唯一の違いは、通常の2Dテクスチャではなく、立方深度マップにレンダリングすることです。



ソースを基準とした方向からシーンの直接レンダリングを開始する前に、適切な変換マトリックスを準備する必要があります。

光源座標系に変換

準備されたフレームバッファオブジェクトとキュービックマップを使用して、すべてのシーンオブジェクトを光源からの6つの方向すべてに対応する座標空間に変換する問題に移ります。 前のレッスンと同じ方法で変換行列を作成しますが、今回は各面に個別の行列が必要です。



ソース空間への各最終変換には、射影行列と種行列の両方が含まれます。 射影行列の場合、透視投影行列を使用します。ソースは空間内のポイントなので、透視投影はここで最適です。 このマトリックスは、すべての最終的な変換で同じになります。

 float aspect = (float)SHADOW_WIDTH/(float)SHADOW_HEIGHT; float near = 1.0f; float far = 25.0f; glm::mat4 shadowProj = glm::perspective(glm::radians(90.0f), aspect, near, far);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

重要な点に注意してください：マトリックス形成中の視野角のパラメーターは90°に設定されます。 この視角の値により、立方体マップの面を正確に塗りつぶしてギャップなしで収束できるようにする投影法が提供されます。



射影行列は一定のままなので、同じ行列を再利用して、最終的な変換の6つの行列すべてを作成できます。 ただし、種マトリックスは、各ファセットに固有のものが必要です。 glm :: lookAtを使用して、次の順序で6つの方向を表す6つの行列を作成します：右、左、上、下、顔に近い、遠い側：

 std::vector<glm::mat4> shadowTransforms; shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3( 1.0, 0.0, 0.0), glm::vec3(0.0,-1.0, 0.0)); shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3(-1.0, 0.0, 0.0), glm::vec3(0.0,-1.0, 0.0)); shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 1.0, 0.0), glm::vec3(0.0, 0.0, 1.0)); shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3( 0.0,-1.0, 0.0), glm::vec3(0.0, 0.0,-1.0)); shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 0.0, 1.0), glm::vec3(0.0,-1.0, 0.0)); shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 0.0,-1.0), glm::vec3(0.0,-1.0, 0.0));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

上記のコードでは、作成された6つのビューマトリックスに投影マトリックスを乗算して、光源の空間に変換する6つの一意のマトリックスを指定しています。 glm :: lookAtの呼び出しのターゲットパラメーターは、キュービックマップの各面を見る方向を表します。



さらに、この行列のリストは、キュービック深度マップをレンダリングするときにシェーダーに渡されます。

デプスシェーダー

立方体マップに深度を書き込むには、頂点、フラグメント、およびこれらのステージ間で実行される追加のジオメトリの3つのシェーダーを使用します。



ワールド空間のすべての頂点を光源の6つの個別の空間に変換するのは、ジオメトリシェーダーです。 したがって、頂点シェーダーは簡単で、幾何学的シェーダーに送られるワールド空間の頂点の座標を単純に提供します。

 #version 330 core layout (location = 0) in vec3 aPos; uniform mat4 model; void main() { gl_Position = model * vec4(aPos, 1.0); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ジオメトリシェーダーは、入力で三角形の3つの頂点と、光源の空間への変換行列の配列を持つユニフォームを受け取ります。 ここに興味深い点があります。ワールド座標からソース空間への頂点の変換を処理するのは幾何学的シェーダーです。



ジオメトリシェーダーの場合、組み込み変数gl_Layerを使用できます 。これは、シェーダーがプリミティブを形成するキュービックマップの面番号を設定します。 通常の状況では、シェーダーはアクションなしでパイプラインにすべてのプリミティブを送信します。 しかし、この変数の値を変更することにより、処理された各プリミティブを3次マップのどの面にレンダリングするかを制御できます。 もちろん、これはキュービックカードがフレームバッファに接続されている場合にのみ機能します。

 #version 330 core layout (triangles) in; layout (triangle_strip, max_vertices=18) out; uniform mat4 shadowMatrices[6]; //  FragPos     //      EmitVertex() out vec4 FragPos; void main() { for(int face = 0; face < 6; ++face) { //  ,    //      gl_Layer = face; for(int i = 0; i < 3; ++i) //      { FragPos = gl_in[i].gl_Position; gl_Position = shadowMatrices[face] * FragPos; EmitVertex(); } EndPrimitive(); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

表示されるコードは非常に簡単です。 シェーダーは、入力で三角形タイプのプリミティブを受け取り、結果として6つの三角形（6 * 3 = 18頂点）を生成します。 メイン関数では、キュービックマップの6つの面すべてをループし、現在のインデックスを、 gl_Layer変数の対応するエントリを持つキュービックマップのアクティブな面の番号として設定します。 また、各入力頂点をワールド座標系から立方体アートの現在の面に対応する光源の空間に変換します。 これを行うには、FragPosにshadowMatrices 均一配列からの適切な変換行列を乗算します。 FragPos値はフラグメントシェーダーにも渡され、フラグメントの深さが計算されることに注意してください。



前回のレッスンでは、空のフラグメントシェーダーを使用し、OpenGL自体はシャドウマップの深度の計算に忙しかった。 今回は、フラグメントの位置と光源の間の距離を基準として、線形深度値を手動で作成します。 深度値のこのような計算により、後続のシェーディング計算がもう少し直感的になります。

 #version 330 core in vec4 FragPos; uniform vec3 lightPos; uniform float far_plane; void main() { //       float lightDistance = length(FragPos.xyz - lightPos); //    [0, 1]    far_plane lightDistance = lightDistance / far_plane; //       gl_FragDepth = lightDistance; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ジオメトリシェーダーのFragPos変数、ソース位置ベクトル、および光源の投影のピラミッドのファークリッピングプレーンまでの距離は、フラグメントシェーダーの入力に到達します。 このコードでは、フラグメントとソース間の距離を計算し、値の範囲[0.、1.]に移動して、シェーダーの結果として書き込みます。



これらのシェーダーとフレームバッファーオブジェクトに接続されたキュービックマップを持つシーンレンダラーは、次のレンダーパスで使用するために完全に準備されたシャドウマップを生成する必要があります。

全方向シャドウマップ

すべてが準備できたら、全方向シャドウの直接レンダリングに進むことができます。 手順は、方向性シャドウの前のレッスンで示した手順と似ていますが、今回は深度マップとして2次元テクスチャの代わりに立方体テクスチャを使用し、光源の投影ピラミッドの遠方面の値を持つユニフォームをシェーダーに転送します。

 glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT); glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); shader.use(); // ...      (      far_plane) glActiveTexture(GL_TEXTURE0); glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap); // ...   RenderScene();
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この例では、renderScene関数は大きな立方体の部屋にあるいくつかの立方体を表示し、シーンの中央にある光源から影を落とします。



頂点シェーダーとフラグメントシェーダーは、方向性シャドウのレッスンで説明したものとほとんど同じです。 フラグメントシェーダーでは、シャドウマップからの選択が方向ベクトルを使用して行われるようになったため、光源の空間におけるフラグメントの位置の入力パラメーターは不要になりました。



頂点シェーダーはそれぞれ、位置ベクトルを光源の空間に変換する必要がないため、 FragPosLightSpace変数を捨てることができます。

 #version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; layout (location = 2) in vec2 aTexCoords; out vec2 TexCoords; out VS_OUT { vec3 FragPos; vec3 Normal; vec2 TexCoords; } vs_out; uniform mat4 projection; uniform mat4 view; uniform mat4 model; void main() { vs_out.FragPos = vec3(model * vec4(aPos, 1.0)); vs_out.Normal = transpose(inverse(mat3(model))) * aNormal; vs_out.TexCoords = aTexCoords; gl_Position = projection * view * model * vec4(aPos, 1.0); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

フラグメントシェーダーのBlinn-Fongライティングモデルコードは変更されず、最後にシェーディング係数による乗算が残ります。

 #version 330 core out vec4 FragColor; in VS_OUT { vec3 FragPos; vec3 Normal; vec2 TexCoords; } fs_in; uniform sampler2D diffuseTexture; uniform samplerCube depthMap; uniform vec3 lightPos; uniform vec3 viewPos; uniform float far_plane; float ShadowCalculation(vec3 fragPos) { [...] } void main() { vec3 color = texture(diffuseTexture, fs_in.TexCoords).rgb; vec3 normal = normalize(fs_in.Normal); vec3 lightColor = vec3(0.3); //   vec3 ambient = 0.3 * color; //   vec3 lightDir = normalize(lightPos - fs_in.FragPos); float diff = max(dot(lightDir, normal), 0.0); vec3 diffuse = diff * lightColor; //   vec3 viewDir = normalize(viewPos - fs_in.FragPos); vec3 reflectDir = reflect(-lightDir, normal); float spec = 0.0; vec3 halfwayDir = normalize(lightDir + viewDir); spec = pow(max(dot(normal, halfwayDir), 0.0), 64.0); vec3 specular = spec * lightColor; //   float shadow = ShadowCalculation(fs_in.FragPos); vec3 lighting = (ambient + (1.0 - shadow) * (diffuse + specular)) * color; FragColor = vec4(lighting, 1.0); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また、いくつかの微妙な違いにも注意してください。照明モデルのコードは実際には変更されていませんが、 samplerCubemapタイプが使用され 、 ShadowCalculation関数は光源のスペースではなくワールド座標でフラグメントの座標を取得します。 また、さらなる計算でfar_plane光源投影ピラミッドパラメーターを使用します。 シェーダーの最後で、シェーディングファクターを計算します。これは、フラグメントがシャドウ内にある場合は1です。 または、フラグメントがシャドウの外側にある場合は0。 この係数は、照明の拡散およびミラーコンポーネントの準備値に影響を与えるために使用されます。



最大の変更点は、 ShadowCalculation関数の本体に関係します。ここでは、深度値が2Dテクスチャではなくキュービックマップから選択されるようになりました。 この関数のコードを順番に分析してみましょう。



最初のステップは、キュービックマップから直接の深度値を取得することです。 覚えているように、キュービックマップの準備では、その深さを書き留めました。これは、フラグメントと光源の間の距離として表されます。 同じアプローチがここで使用されます：

 float ShadowCalculation(vec3 fragPos) { vec3 fragToLight = fragPos - lightPos; float closestDepth = texture(depthMap, fragToLight).r; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

フラグメントの位置と光源の間の差ベクトルが計算され、キュービックマップからのサンプリングの方向ベクトルとして使用されます。 思い出すように、キュービックマップからのサンプルベクトルは単位長さを持つ必要はなく、それを正規化する必要はありません。 結果として最も近いDepthDepth値は、光源に対して最も近い可視フラグメントの正規化された深度値です。



nearestDepthの値は区間[0.、1.]にあるため、最初に区間[0.、 far_plane ]への逆変換を実行する必要があります。

 closestDepth *= far_plane;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、光源に対する現在のフラグメントの深度値を取得します。 選択したアプローチの場合、それは非常に簡単です。すでに準備されているfragToLightベクトルの長さを計算するだけです。

 float currentDepth = length(fragToLight);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、我々は、 closethDepthと同じ（そして、おそらく、より大きな）間隔にある深度値を取得します。



これで、現在のフラグメントがシャドウ内にあるかどうかを調べるために、両方の深度を比較することができます。 また、 前のレッスンで説明した「シャドウリップル」問題が発生しないように、比較にオフセット値をすぐに含めます。

 float bias = 0.05; float shadow = currentDepth - bias > closestDepth ? 1.0 : 0.0;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

完全なShadowCalculationコード：

 float ShadowCalculation(vec3 fragPos) { //          vec3 fragToLight = fragPos - lightPos; //        //        float closestDepth = texture(depthMap, fragToLight).r; //       [0,1] //       closestDepth *= far_plane; //        //        float currentDepth = length(fragToLight); //   float bias = 0.05; float shadow = currentDepth - bias > closestDepth ? 1.0 : 0.0; return shadow; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

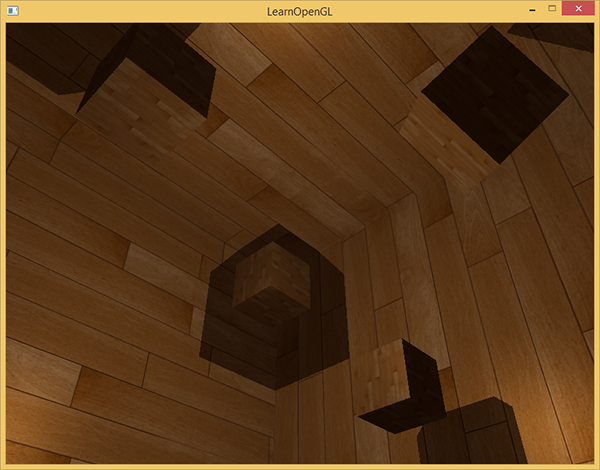
指定されたシェーダーを使用すると、アプリケーションはすでにかなり許容できるシャドウを表示し、今回はソースからすべての方向に投影されます。 ソースが中央にあるシーンの場合、画像は次のように表示されます。











完全なソースコードはこちらです。

深さの3次マップの可視化

あなたが私といくらか似ているなら、私は、あなたが最初はすべてを正しく行うことができないだろうと思うので、アプリケーションをデバッグするいくつかの手段は非常に有用でしょう。 最も明白なオプションとして、深度マップの準備の正確性を検証できると便利です。 現在は2次元のテクスチャではなく立方体のマップを使用しているため、視覚化の問題にはもう少し複雑なアプローチが必要です。



簡単な方法は、 ShadowCalculation関数の本体から正規化されたnearestDepth値を取得し、フラグメントシェーダーの結果として出力することです。

 FragColor = vec4(vec3(closestDepth / far_plane), 1.0);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果はグレースケールのシーンになり、色の強度はこのシーンの線形深度値に対応します。









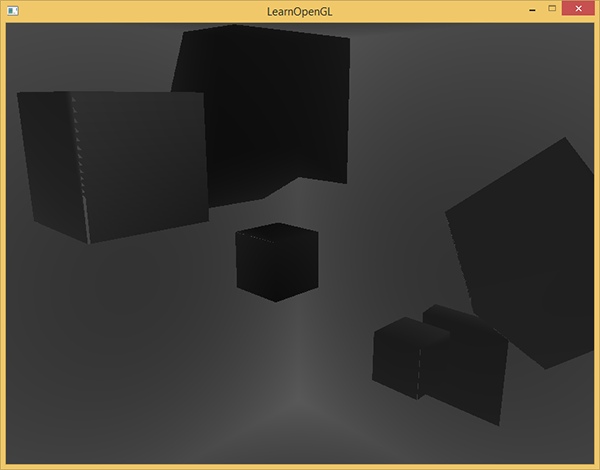
部屋の壁の陰影領域も表示されます。 視覚化の結果が与えられたものと類似している場合、シャドウマップが正しく準備されていることを確認できます。 そうしないと、エラーがどこかに忍び込んでしまいました。たとえば、値nearestDepthは間隔[0.、 far_plane ]から取得されました。

近いパーセンテージのフィルタリング

全方向性シャドウは、方向性シャドウと同じ原理に基づいて構築されているため、テクスチャ解像度の精度と有限性に関連するすべてのアーティファクトを継承しました。 影付きの領域の境界に近づくと、ギザギザのエッジが見られます。 エイリアシングアーティファクト。 Percentage-closer filtering （ PCF ） フィルタリングを使用すると、現在のフラグメントの周囲の複数の深度サンプルをフィルタリングし、深度比較結果を平均化することにより、エイリアシングトレースをスムーズにできます。



前のレッスンのPCFコードを取得し、3番目の次元を追加します（3次マップのサンプルには方向ベクトルが必要です）。

 float shadow = 0.0; float bias = 0.05; float samples = 4.0; float offset = 0.1; for(float x = -offset; x < offset; x += offset / (samples * 0.5)) { for(float y = -offset; y < offset; y += offset / (samples * 0.5)) { for(float z = -offset; z < offset; z += offset / (samples * 0.5)) { float closestDepth = texture(depthMap, fragToLight + vec3(x, y, z)).r; closestDepth *= far_plane; //     [0;1] if(currentDepth - bias > closestDepth) shadow += 1.0; } } } shadow /= (samples * samples * samples);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

違いはほとんどありません。 各軸で作成するサンプルの数に基づいて、テクスチャ座標の変位を動的に計算し、キューブ化されたサンプルの数で割って結果を平均します。



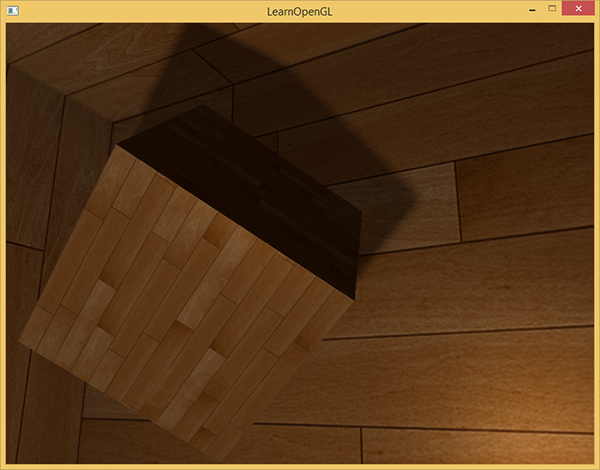
これで、シャドウはより本物に見え、エッジは非常に滑らかになりました。









ただし、サンプルの数をsample = 4に設定すると、実際には各フラグメントに64個ものサンプルを費やすことになり、これは非常に多くなります。



また、ほとんどの場合、これらのサンプルは元のベクトルに非常に近いため、冗長になります。 おそらく、サンプルの元のベクトルに垂直な方向にサンプルを作成する方が便利でしょう。 残念ながら、生成された追加の方向のどれが冗長になるかを見つけるための簡単な方法は存在しません。 1つの手法を使用して、バイアス方向の配列を自問することができます。バイアス方向はすべて、ほぼ完全に分離可能なベクトルです。 それぞれが完全に異なる方向を指します。 これにより、互いに近すぎるバイアス方向の数が減少します。 以下は、20の特別に選択された変位方向を持つ同様の配列です。

 vec3 sampleOffsetDirections[20] = vec3[] ( vec3( 1, 1, 1), vec3( 1, -1, 1), vec3(-1, -1, 1), vec3(-1, 1, 1), vec3( 1, 1, -1), vec3( 1, -1, -1), vec3(-1, -1, -1), vec3(-1, 1, -1), vec3( 1, 1, 0), vec3( 1, -1, 0), vec3(-1, -1, 0), vec3(-1, 1, 0), vec3( 1, 0, 1), vec3(-1, 0, 1), vec3( 1, 0, -1), vec3(-1, 0, -1), vec3( 0, 1, 1), vec3( 0, -1, 1), vec3( 0, -1, -1), vec3( 0, 1, -1) );
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

さらに、PCFアルゴリズムを変更して、キュービックマップから取得するプロセスでsampleOffsetDirectionsなどの固定サイズの配列を使用できます。このアプローチの主な利点は、最初のアプローチと視覚的には似ていますが、必要な追加サンプルの数が大幅に少ない結果を作成できることです。

 float shadow = 0.0; float bias = 0.15; int samples = 20; float viewDistance = length(viewPos - fragPos); float diskRadius = 0.05; for(int i = 0; i < samples; ++i) { float closestDepth = texture(depthMap, fragToLight + sampleOffsetDirections[i] * diskRadius).r; closestDepth *= far_plane; //     [0;1] if(currentDepth - bias > closestDepth) shadow += 1.0; } shadow /= float(samples);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

上記のコードでは、変位ベクトルにdiskRadius値が乗算されています。これは、元のfragToLightサンプルベクトルの周囲に構築され、追加のサンプルが作成されるディスクの半径を表します。



さらに進んで次のトリックを実行できます。フラグメントからのオブザーバーの距離に応じてdiskRadius値を変更してみてください。そのため、変位の半径を大きくし、遠くの破片では影を柔らかくし、観察者に近い破片ではよりシャープにすることができます。

 float diskRadius = (1.0 + (viewDistance / far_plane)) / 25.0;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このようなPCFアルゴリズムの結果は、元のアプローチよりも劣らないソフトシャドウを生成します。









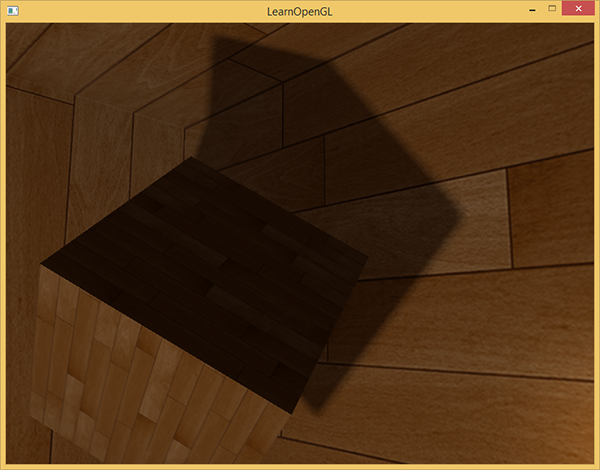
もちろん、各フラグメントに追加されるバイアス値は、シーンのコンテキストとコンテンツに大きく依存しているため、常に追加の実験設定が必要になります。提案されたアルゴリズムのパラメーターを試して、最終的な画像への影響を確認します。



この例のソースコードはこちらにあります。



また、幾何学的シェーダーを使用して立方体の深度マップを作成することは、各面のシーンを6倍にレンダリングするよりも必ずしも高速ではないことに注意してください。このアプローチを使用すると、パフォーマンスにマイナスの影響があります。一般に、パフォーマンスへのマイナスの寄与が、ジオメトリシェーダーと1回の描画呼び出しを使用するすべての利点を上回る可能性があります。そして、もちろん、それはあなたがどの環境で働いているか、どのビデオカードとどのドライバがあなたに利用可能か、そして他の多くのものに依存します。したがって、パフォーマンスが本当に重要な場合、検討中のすべての選択肢をプロファイルし、アプリケーションのシーンで最も効果的であることが判明した選択肢を選択することは常に価値があります。個人的には、シャドウマップを作成するタスクでのジオメトリシェーダーの使用を固守しています。これは、シャドウシェーダーの使用がより直感的だからです。

追加資料：

• OpenGLの点光源のシャドウマッピング：sunandblackcatの全方向シャドウマップのチュートリアル。
• ポイントライトを使用したマルチパスシャドウマッピング：同様ですが、ogldevの作成者によるものです。
• 全方向シャドウ：Peter Houskaによる全方向シャドウマップに関する楽しいプレゼンテーション。

PS ：転送を調整するための電報confがあります。 翻訳を手伝いたいという真剣な願望があれば、大歓迎です！