まず第一に、スクーターは私のものではありません。 記事に記載されている回路は、Caroline ColillinとGiovanni Plazotta(C. Colijn、G。Plazzotta) によってSystematic Biologyで公開されました。 しかし、ほとんどのhabrは英語の生物学雑誌を読むことはまずないので、そこから翻訳する価値があると判断しました。
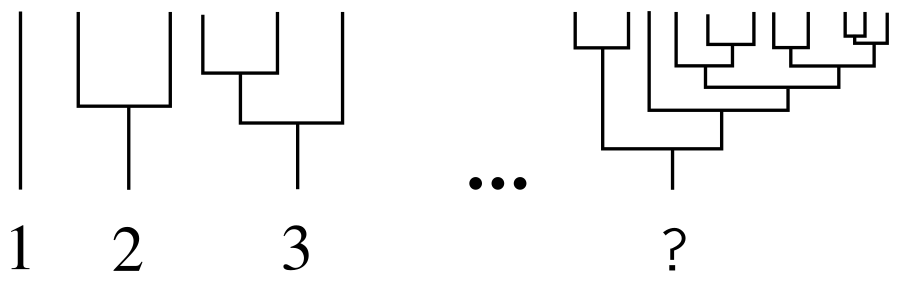
既に特定の番号付けスキームがあり、番号付けは1枚のシートで構成される単純なツリーから始まると仮定します。 k > = j 、 (k、j)-treeのような番号kとjを持つ2つのサブツリーで構成されるツリーを呼び出します。 ( k 、 j )-treesのセットを辞書式に設定します:(1)、(1、1)、(2、1)、(2、2)、(3、1)、(3、2)...目的の数は正確にその順序でツリーのための場所があります。 つまり、(1、1)-treeはツリー番号2と同じです。(2、1)-treeはツリー番号3と同じです。 次のことを確認できます。KDPVではそのままです。
( k、j )表記を数値に変換するには、これが本質的にすべての自然数の可能なペアのシーケンスであるという事実に注意する必要があります。 定義によりk > = j > = 1であるため、任意のkに対して ( k 、1)から( k 、 k )までの正確にk ( k 、 j )ペアが存在します。 したがって、( k 、1)-pairの番号は(1 + 2 + 3 + ... + k -1)+ 1になります。これは、(1 + 2 + 3 + ... + k -1)ペアが先行するためです。 そして、もちろん、( k 、 j )-pairsの数は、( k 、1)-pairsの数よりも( j -1)大きくなります。 算術級数の合計の式を代入し、余分な単位を減らすと、次の式が得られます。
N(k、j)= dfrack(k−1)2+j+1
余分な単位は、シーケンスが(1、1)-ではなく(1)-treeで始まるという事実によって説明されます。 これで、任意のツリーの数を再帰的に計算できます。 ターゲットツリーは、定義によりa( k 、 j )-treeです。ここで、 kとjはそのルートから成長するサブツリーです。 同様に、 kツリーは( k1 、 k2 )ツリーです。ここで、 k1とk2はそのサブツリーであり、同様に(1)ツリーである葉まで続きます。 例:
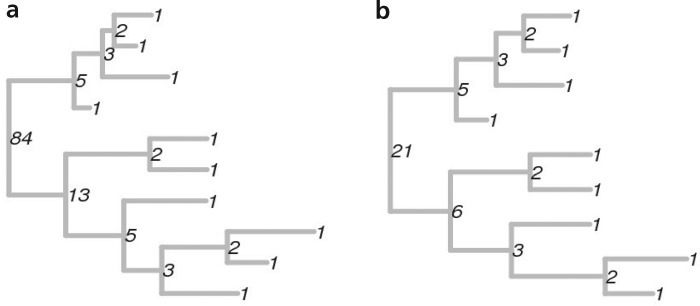
この数の計算方法から、事業全体の実際的な意味に従います。 実際、数字は素晴らしいものですが、次に何をすべきかはあまり明確ではありません。 膨大な数がRAM全体を占有し 、さらに多くを必要とすることを賞賛する場合を除き (実際には、500本の葉で1ダースほどの木をマークアップしても、 gmpy2を使用しても64 GBに収まりません)。 それらは、木にわずかな変化があっても大きく変化します。 たとえば、上の図の2つのツリーの違いは、右の一番下に1つのシートがないことだけです。 しかし、各ツリーには、すべての内部ノードの数のベクトルもあります。 また、ベクトルでは、距離メトリック(ユークリッドなど)を定義し、それを使用してツリートポロジをクラスター化することが既に可能です。 元の記事では、樹木は系統発生的であり、米国と熱帯地方でのインフルエンザウイルスの進化の違いを特定することができました。 熱帯地方では、病気は一年中発生するため、すべての中間形態が観察されます(右側の( k 、1)-木の質量)。 しかし、アメリカでは、インフルエンザは季節的な問題であり、主に海外から持ち込まれているため、実際にはそのような木はありません。
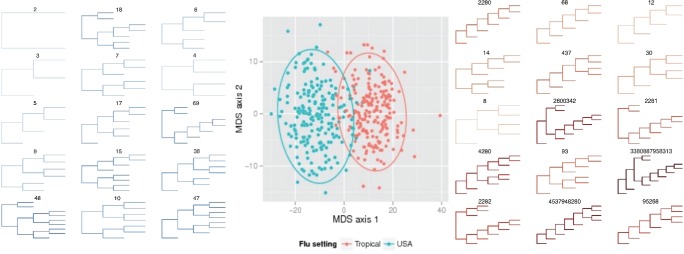
元の記事にはまだ多くの興味深いことがあります:特に、非バイナリツリーの一般化、距離メトリックのさまざまな実用的なオプション、これらが厳密な意味でのメトリックであることの証明、ツリーの数学演算の定義など。 突然プレイしたい場合は、Rの作成者コードとpython実装がgithubで利用可能です。 ただし、どちらも系統樹用に設計されています。