コントローラー設定を計算するためのPythonフリーの方法

はじめに

非検索法は、PD、PDD、PIDDなどのアルゴリズムを含む、準最適なコントローラーの設定を計算するための、シンプルで信頼性の高い普遍的な方法です[1]。



ただし、[1]で説明されているこの方法のソフトウェア実装には多くの欠点があり、マイクロプロセッサ制御デバイスでの使用が複雑になっています。



次のような欠点を特定できます。



コントローラーの伝達関数の構造に平滑化リンクがある場合でも、負の設定につながる可能性のある動作周波数の範囲を決定する際のあいまいさ。



[1]では、レギュレーターを計算するための非検索方法を実装するために、フォームのオブジェクトの伝達関数が考慮されます。







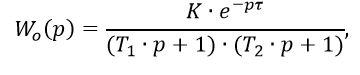
分母の演算子pの2次では、制御オブジェクトの動的識別の精度が制限される[2]。

問題文：

1.高レベルのプログラミング言語Pythonを使用して、最大周波数で伝達関数の虚数部と実数部が正になるように、準最適コントローラーCFCから最大および最小周波数値を決定します。



2. scipyライブラリの手段。 準最適レギュレーターの伝達関数によって見つかった高水準プログラミング言語Pythonを最適化して、レギュレーターを調整し、scipyライブラリーを使用します。 統合して、閉制御システムの過渡特性を取得します。



3.オブジェクトをより正確に識別するには、計算で伝達関数を使用します。これは、分母に演算子pの3乗があります。







4.検索[3]と非検索方法によって得られた閉システムの過渡特性を比較します。



5.非検索法を使用して、PIDDアルゴリズムの遷移特性を構築し、PIDアルゴリズムを使用して制御品質の積分2次基準を使用して比較します。

理論

単一回路のレギ​​ュレーションシステムの構造図を考えてみましょう。







最適なコントローラーアルゴリズムは、ステップ入力エフェクトの適用ポイントによって異なります。 次の図は、アクションに関する閉ループシステムの過渡特性を示しています。a）─マスター（t）; b）─外部v（t）; c）─内部λ（t）：







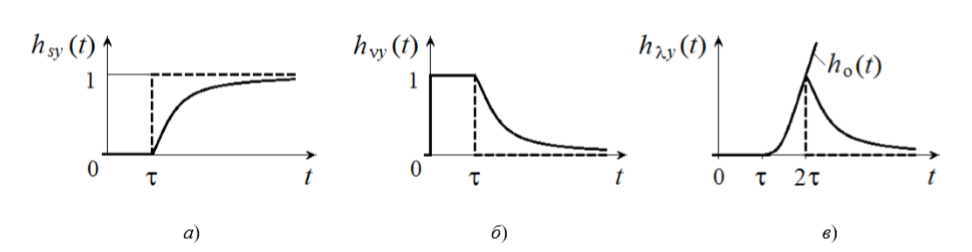
遅延時間τが経過した後、最適なコントローラーは、システム入力で与えられたユニットアクションs（t）= 1を完全に再現する必要があります。 このため、閉じたシステムの伝達関数は次と等しくなければなりません。







上記の方程式から、最適なコントローラーの伝達関数の比率を取得します。



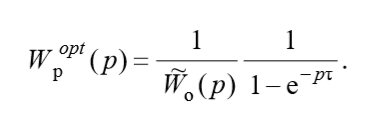（1）



複素周波数応答（1）では、周期τのギャップがあり、システムの安定性が失われます。 したがって、次善のコントローラーの伝達関数を取得するには、伝達関数で最も単純な慣性要素を使用して平滑化を適用する必要があります。







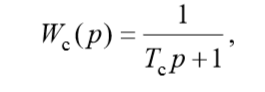
次に、次善の閉システムの望ましい伝達関数は次のように表すことができます。







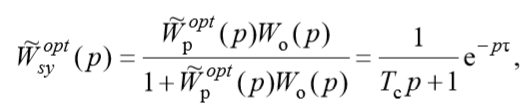
準最適レギュレーターの伝達関数は



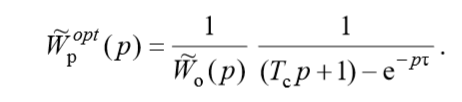（2）



準最適なコントローラーの構造はオブジェクトの伝達関数の構造に依存するため、準最適なコントローラー（2）の伝達関数を使用しても、所望の過渡プロセスが得られない場合があります。



たとえば、過熱蒸気の温度を制御する場合、オブジェクトには極端な過渡応答があります。 この場合、平滑化として、伝達関数で積分微分（ID）リンクを選択する必要があります。







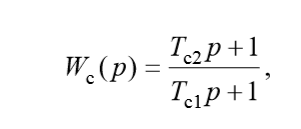
次に、次善のコントローラーの伝達関数は次のように記述されます。



（3）



準最適なコントローラー（2）、（3）の伝達関数を使用して、設定を決定するための無探索法の検討に進むことができます。



サーチレス法による線形レギュレーターの最適設定の計算[1]：



準最適な（2）または（3）コントローラーの周波数特性の最小二乗近似は、それぞれ4つのc1、c2、c3、c4および3つのc1、c2、c3設定を持つPIDDおよびPIDコントローラーの例を使用して実行されます。



PIDコントローラーの特別なケースは、P、PI、PD、およびSDAの規制法です。 Pコントローラの場合、PI-c3、c4、PD ― c2、c4、およびトラフィックルールc2の設定、c2、c3、c4を0に等しくする必要があります。



CFCリニアPIDDコントローラーは次の形式で表示されます。



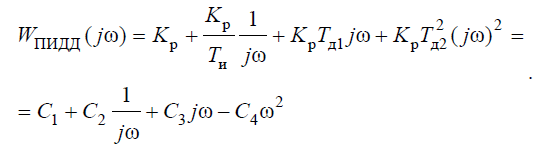（4）







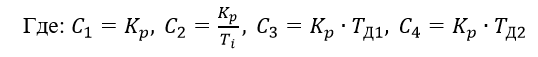
すべてのタイプのコントローラーの周波数特性のN個のベクトルの残差の二乗和を記述します

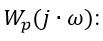
Pythonサーチレスメソッドの実装

動作周波数の最大値と最小値の準最適レギュレーターのCFCによる決定：

# -*- coding: utf8 -*- import numpy as np from scipy.integrate import quad from scipy.optimize import * import matplotlib.pyplot as plt T1=14;T2=18;T3=28;T=15;K=0.9;tau=6.4#  (       ) fmin=0.004#     fmax=0.08#    df=0.0001#   n=np.arange(fmin,fmax,df)#   def W(w):#   j=(-1)**0.5 return ((K*(np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1)))) def WO(w):#      j=(-1)**0.5 return (1/(K*(T*j*w+1-np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1)))) def ReWO(w):#      j=(-1)**0.5 return WO(w).real def ImWO(w):#      j=(-1)**0.5 return WO(w).imag S1=[ReWO(w) for w in n] S2=[ImWO(w) for w in n] plt.title("     \n    ") plt.xlabel("Re(WO)") plt.ylabel("Im(WO)") plt.plot(ReWO(min(n)),ImWO(min(n)),'o',label=' -(%s,%s)'%(round(ReWO(min(n)),1),round(ImWO(min(n)),1))) plt.plot(ReWO(max(n)),ImWO(max(n)),'o',label=' -B(%s,%s)'%(round(ReWO(max(n)),1),round(ImWO(max(n)),1))) plt.plot(S1,S2) plt.grid(True) plt.legend(loc='best') plt.show()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

変数fmin、fmax、dfを使用してCFCの必要なセクションを見つけた後、次のように取得します。







例として、分母のp演算子の3乗を使用して、PIDコントローラーとオブジェクトの伝達関数を使用した検索および非検索方法の比較分析：



非検索と検索方法の比較分析のために、オブジェクトパラメータT1 = 14に対して、私の出版物[3]に記載されている検索方法の結果を使用します。 T2 = 18; T3 = 28; K = 0.9; 最初の問題を解決するために使用されたtau = 6.4。





テキスト出力結果：



PIDコントローラーの設定番号1（wa = 0.066、m = 0.366、alfa = 0.7）：Kr = 4.77; Ti = 21.682; Ki = 0.22; Td = 15.177

PIDコントローラーの設定番号2（wa = 0.056、m = 0.366、アルファ= 0.2）：Kr = 2.747; Ti = 50.87; Ki = 0.054; Td = 10.174

PIDコントローラーの設定番号3（wa = 0.085、m = 0.366、アルファ= 0.7）：Kr = 3.747; Ti = 26.387; Ki = 0.142; Td = 18.471

線形積分品質基準I1 = 194.65（設定番号1）

二次積分品質基準I2 = 222.428（設定番号1

線形積分品質基準I1 = 179.647（設定番号2）

二次積分品質基準I2 = 183.35（設定番号2）

線形積分品質基準I1 = 191.911（設定番号3）

二次積分品質基準I2 = 204.766（設定番号3）

積分基準による最適パラメーター：

PIDコントローラーの設定番号2（wa = 0.056、m = 0.366、アルファ= 0.2）：Kr = 2.747; Ti = 50.87; Ki = 0.054; Td = 10.174





取得するもの：



サーチレス法の目標関数の推定値：484.254

サーチレス法によるPIDコントローラー設定：Kp = 2.22; Ti = 42.904; Ki = 0.052; Td = 27.637

検索方法によるPIDコントローラー設定：Kp = 2.747; Ti = 50.87; Ki = 0.054; Td = 10.174

検索方法の目標関数の推定値[3]：2723.341







明らかに、サーチレス方式の方が実装が簡単で、規制品質が向上します。



設定の計算と非標準PIDD規制アルゴリズムのクローズドシステムの過渡応答の取得：

  # -*- coding: utf8 -*- import numpy as np from scipy.integrate import quad from scipy.optimize import * import matplotlib.pyplot as plt T1=14;T2=18;T3=28;T=15;K=0.9;tau=6.4 fmin=0.004 fmax=0.08 df=0.0001 n=np.arange(fmin,fmax,df) def W(w):#   j=(-1)**0.5 return ((K*(np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1)))) def WO(w):#    j=(-1)**0.5 return (1/(K*(T*j*w+1-np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1)))) def WR(w,c1,c2,c3,c4):#    j=(-1)**0.5 return (c1+c2/(j*w)+c3*j*w-c4*w**2) def NF(c1,c2,c3,c4): return sum([((WO(w)).real-WR(w,c1,c2,c3,c4).real)**2+((WO(w)).imag-WR(w,c1,c2,c3,c4).imag)**2 for w in n]) def fun2(x): return NF(*x) x0=[1,1,1,1] res = minimize(fun2, x0) time=np.arange(0,300,1) e1=round(res['x'][0],3) e2=round(res['x'][1],3) e3=round(res['x'][2],3) e4=round(res['x'][3],3) print ("      :",round(res['fun'],3)) def h(t,e1,e2,e3,c4): return quad(lambda w:(2/np.pi)*(((W(w))*WR(w,e1,e2,e3,e4))/(1+(W(w))*WR(w,e1,e2,e3,e4))).real*(np.sin(w*t)/w),0,max(n))[0] h1=[h(t,e1,e2,e3,e4) for t in time] I1=round(quad(lambda t:h(t,e1,e2,e3,e4), 0,300)[0],3)+round(quad(lambda t: h(t,e1,e2,e3,e4)**2,0, 300)[0],3) plt.title("     ") plt.plot(time,h1,'r',linewidth=2,label='    - %s'%I1) plt.legend(loc='best') plt.grid(True) plt.show()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

取得するもの：



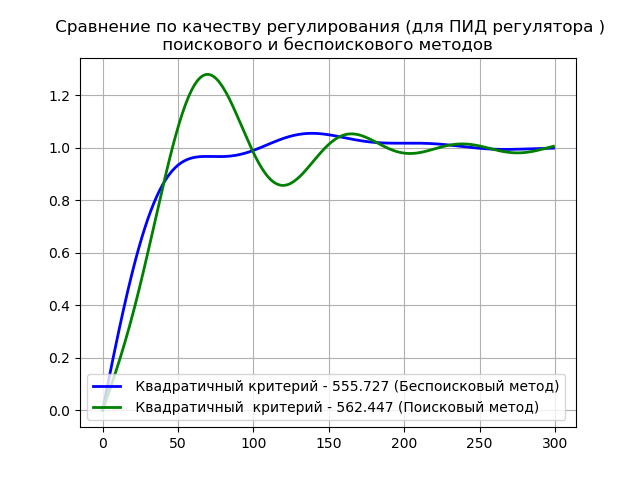
サーチレス法の目標関数の推定値：0.326







予想どおり、PIDDアルゴリズムはPIDよりも優れた制御品質を提供しますが、準最適なコントローラーに対する最大近似を備えています。



リストされたプログラムリストは、規制法の規制当局、、およびに簡単に変換できます。 Pコントローラの場合、PI-c3、c4、PD ― c2、c4、およびトラフィックルールc2の設定、c2、c3、c4を0に等しくする必要があります。

結論：

最小2次基準のコントローラー設定を計算するための非検索方法のPython実装の利点が考慮されます。

参照：

1. レギュレータ設定を最小二次基準まで計算するための非検索方法。



2. 制御オブジェクトの動的な識別。



3. 制御品質の積分基準によるPIDコントローラー設定の最適化。