最初に、最も単純な動作を検討します。シーケンシャル、サイクリック、各信号はサイクルごとに正確に2回切り替わります。 振る舞いを文字列の形式で、左から右への方向で示します。 省略記号は、この場所でいくつかの信号の切り替えのシーケンスが可能であることを意味します。
状態がグラフ上でどのように見えるかから始めましょう。

状態は、2つのイベント間のドット(赤)です。 この場合、a = 0、b = 1、c = 0、d = 1です。 STGでは、状態はラベル付きの目印のセットです。
次に、単純なインプリカントがグラフでどのように見えるかを見てみましょう。 接続詞(関数AND)を検討します。
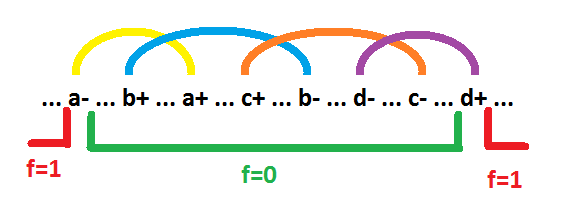
含意者が0に等しいゾーンは緑で強調表示され、含意者が1に等しいゾーンは赤で強調表示されます。 このゾーンの外側のすべてのスペースは、インターセプトのチェーンです。 このチェーンのリンク(グラフの上に表示)は、含意を形成する信号を切り替えることで形成されます。 各リンクは、1つの信号を切り替えるペアです。 このリンク内の状態でリンクを形成する信号は、0に等しい暗黙の値を維持します。単位ゾーン(したがって、ゼロのゾーン)は不連続になる可能性があります。 しかし、これまでのところ、そのような機会を考慮する必要はありません。 受け入れられた条件の下では、単純な暗黙的要素のインターセプトチェーンのそのような構造が唯一可能な構造です。 たとえば、c +イベントがa +イベントの左側にある場合、信号bは暗黙的に削除されます。 将来的には、インプラントとは、特定の含意者のユニットのゾーンを意味します。 インターセプトチェーンの極端なイベントは、インプラントの境界と呼ばれます。 図では、イベントd +は左の境界、イベントa-は右の境界です。 どの信号が反転を伴ってインプリカントに入力され、どの信号が反転されないかを調べることは残っています。 リンクが「-」イベントで始まる場合、信号は反転せずにインプリカントに入ります(図では、信号aとd)。 リンクが「+」イベントで始まる場合、信号は反転してインプリカントに入ります(図の信号bとc)。 その結果、図は、暗黙のa *!B *!C * dの動作を示しています。
それでは、インプラントの作成に移りましょう。 まず、質問に答えます:論理関数の計算に関して、インプリカントの主な特徴は何ですか? これらは、この暗黙の要素を構成する変数(シグナル)のように思われます。 しかし、実際には、インプラントの主な特徴は、行動グラフ上の位置です(ユニットゾーンの位置について合意したように)。 そして、インプラントを構成する信号は、目的の場所に到達するための手段です。 つまり、インプラントを構築するプロセスは、グラフ上の適切な場所にインプラントを配置するために必要な信号の計算です。 ここで疑問が生じます:インプラントの将来の位置をどのように設定するか? インプラントの位置は3ポイント(状態)で設定されます。

ポイント2は、インプラントが必ず値1をとる必要がある状態です。ポイント1と3は、インプリカントが値1をとることができる極端な状態です。つまり、インプリカントはポイント2を含み、ポイント1と3まで拡張できます。左の境界線は無関心で、右の境界線はポイント2から最大限に離す必要があります。ポイント1と3はポイント2に一致します(一度に2つではなく個別に)
インプラントを構築するプロセスは、信号のシーケンシャル検索-インターセプトチェーンのリンクです。 このプロセスは、右から左に導く方が便利です(この理由は後で説明します)。 検索はポイント1と2の間で始まり、リンクがポイント2と3の間で終わると終了します。このようなインターセプトチェーンを構築できないことは、1つのことだけを意味します。動作にはCSCの競合が含まれます。 最小限の機能のためのインプラントを探しているため、相互に競合する可能性のある2つの要因が重要です:暗黙の変数の数(つまりリンク)とインプラントの長さ(それがカバーする状態のセット)。 したがって、リンクが最も長く選択されます。 後者に加えて、可能な限り短く選択されます。 また、最後のリンクを短いリンクのチェーンで置き換えることができる瞬間を考慮する必要があります。 この場合、インプラント自体の長さが長くなる場合があります。
ここで、単純な暗黙のカバーポイント2を計算するアルゴリズムについて説明します。メモリとして、アルゴリズムは2つのセットを使用します。現在のリンクの場所の候補のセット(セットP)と次のリンクの場所の多くの候補(セットN)。 これらのセットのメンバーの最大数は、信号の数に等しくなります。 最初は、セットは空です。
手順1.ポイント2の左側にあるイベントを考慮します。
ステップ2.問題のイベントがポイント1の左側にある場合、a)問題のイベントに対応する信号がセットPに追加され、b)前のイベントの検討に進みます。
ステップ3.問題のイベントがポイント3の右側にある場合、ステップ15に進みます。
ステップ4.問題のイベントがポイント1の左側にある場合、a)問題のイベントに対応する信号がセットNに属する場合、このセットからこの信号を除外します。それ以外の場合、この信号をこのセットに追加します。 b)セットNが空の場合(これはCSCの競合を意味します)、アルゴリズムを終了します。 c)セットPをセットNと等しくする、d)セットNを空にする、e)前のイベントの検討に進む、e)ステップ3に進む
ステップ5.問題のイベントに対応する信号がセットNに属する場合、a)このセットからこの信号を除外し、b)前のイベントの検討に進み、c)ステップ3に進みます。
ステップ6.問題のイベントに対応する信号がセットPに属さない場合、a)この信号をセットNに追加し、b)前のイベントの検討に進み、c)ステップ3に進みます。
ステップ7.問題のイベントに対応する信号をセットPから削除します。
ステップ8.セットPが空でない場合、a)前のイベントの検討に進み、b)ステップ3に進みます。
ステップ9.問題のイベントに対応する信号は、変数として暗黙的に追加されます。
手順10.セットNが空の場合(CSCの競合)、アルゴリズムを終了します。
手順11.セットPをセットNと等しくします。
ステップ12.セットNを空にします。
ステップ13.前のイベントの検討に進みます。
ステップ14.ステップ3に進みます。
ステップ15.問題のイベントに対応する信号がセットPに属さない場合、a)前のイベントの検討に進み、b)ステップ15を繰り返します。
手順16.問題のイベントに対応する信号が、変数として暗黙的条件に追加されます。
ステップ17.インプリカントが構築されます。 アルゴリズムの完了。
ご覧のとおり、イベントグラフで単純なインプリカントを計算するためのアルゴリズムの複雑さは(許容される条件下で)グラフ内のイベントの数に比例します。 このアルゴリズムは、メモリオーバーヘッドを実質的に必要としません。
このアルゴリズムは、変数の数が最も少ないインプラントを計算するように構成されています。 多くの変数を持つインプラントを取得し、より多くの状態をカバーするには、少し改善する必要があります。 セットPから削除された最後の信号を覚えておく必要があります。 また、その後、セットNからすべての信号が削除されます。 アルゴリズムがステップ15に近づいた後、セットNの削除および保存された信号を復元し、セットPから削除された最後の信号を暗黙的に追加し、信号が最後にセットPから削除された後のイベントから検討を続ける必要があります。 このようにして、すべての極値を見つけることができます。 継続する。