
規制の質を評価する問題の声明
規制の質を総合的に評価することにより、システム内の実際の過渡状態と理想的な過渡状態との合計偏差を特徴付けます。
理想的なプロセスとして、通常、ステップワイズ(ステップワイズ)過渡プロセスまたは指定された指数パラメーターを持つ指数プロセスが採用されます。
これまで、レギュレータの設定を最適化するために、どの基準が線形または二次を選択するかは不明でした。
この出版物では、最適なコントローラー設定は、規制の質の線形および二次積分インジケーターの合計の形で、最適性基準に基づいて決定されます。
このような選択を行うには、微分時定数と積分時定数の比α= Td / Tiの異なる値に対して一連の予備計算を実行し、Kr / Ki比の最高値を提供するαのいくつかの値を選択する必要があります。
その後、レギュレーター設定用のいくつかのオプションを用意し、クローズドシステムでそれらのトランジェントを構築し、提案された基準に従って最適な設定を選択します。
最適なコントローラー設定の計算のソフトウェア実装
計算は、数学パッケージと任意のプログラミング言語の両方で実行できます。 しかし、 数値統合のための強力なライブラリが利用可能であり、リスト内のローカル極値を簡単に検索できるため、高レベルのPythonプログラミング言語を選択しました。
プログラムの最初の検索手順を簡素化するために、初期データを確立し、解決する問題ごとに既成の頻度リストを個別に提供することをお勧めします。
ソースデータの準備
# -*- coding: utf8 -*- import numpy as np # from scipy.integrate import quad # import matplotlib.pyplot as plt # T1=14; T2=18; T3=28; K=0.9; tau=6.4# , , m=0.366; m1=0.221# n= np.arange(0.001,0.15,0.0002)# Kr-Ki n1=np.arange(0.00001,0.12,0.0001) # Ki=f(w) n2=np.arange(0.0002,0.4,0.0001) #
ルート振動指数mを考慮した水熱交換器の伝達関数と、Kr、Ti、Td、およびその他の補助関数を考慮したPIDコントローラーの伝達関数を導入します。
複雑な算術演算を考慮した基本および補助機能の入力
def WO(m,w):# j=(-1)**0.5 return K*np.exp(-tau*(-m+j)*w)/((T1*(-m+j)*w+1)*(T2*(-m+j)*w+1)*(T3*(-m+j)*w+1)) def WR(w,Kr,Ti,Td):# j=(-1)**0.5 return Kr*(1+1/(j*w*Ti)+j*w*Td) def ReW(m,w):# j=(-1)**0.5 return WO(m,w).real def ImW(m,w):# j=(-1)**0.5 return WO(m,w).imag def A0(m,w):# return -(ImW(m,w)*m/(w+w*m**2)+ReW(m,w)/(w+w*m**2)) def Ti(alfa,m,w):# return (-ImW(m,w)-(ImW(m,w)**2-4*((ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m)*A0(m,w)))**0.5)/(2*(ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m)) def Ki(alfa,m,w):# return 1/(w*Ti(alfa,m,w)**2*alfa*(m*ReW(m,w)+ImW(m,w))-Ti(alfa,m,w)*ReW(m,w)+(m*ReW(m,w)-ImW(m,w))/(w+w*m**2)) def Kr(alfa,m,w):# if Ki(alfa,m,w)*Ti(alfa,m,w)<0: z=0 else: z=Ki(alfa,m,w)*Ti(alfa,m,w) return z def Kd(alfa,m,w):# return alfa*Kr(alfa,m,w)*Ti(alfa,m,w)
アルファ= Td / Ti = 0.2、アルファ= Td / Ti = 0.7、アルファ= Td / Ti = 1.2の比率でPIDコントローラーを調整するための3つの平面を構築します。
最適なアルファ値を見つける
alfa=0.2 Ki_1=[Ki(alfa,m1,w) for w in n] Kr_1=[Kr(alfa,m1,w) for w in n] Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] Ki_3=[Ki(alfa,0,w) for w in n] Kr_3=[Kr(alfa,0,w) for w in n] plt.figure() plt.title(" \n alfa=%s"%alfa) plt.axis([0.0, round(max(Kr_3),4), 0.0, round(max(Ki_3),4)]) plt.plot(Kr_1, Ki_1, label=' m=%s'%m1) plt.plot(Kr_2, Ki_2, label=' m=%s'%m) plt.plot(Kr_3, Ki_3, label=' m=0') plt.xlabel(" - Ki") plt.ylabel(" - Kr") plt.legend(loc='best') plt.grid(True) alfa=0.7 Ki_1=[Ki(alfa,0.221,w) for w in n] Kr_1=[Kr(alfa,0.221,w) for w in n] Ki_2=[Ki(alfa,0.366,w) for w in n] Kr_2=[Kr(alfa,0.366,w) for w in n] Ki_3=[Ki(alfa,0,w) for w in n] Kr_3=[Kr(alfa,0,w) for w in n] plt.figure() plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)]) plt.title(" \n alfa=%s"%alfa) plt.plot(Kr_1, Ki_1, label=' m=%s'%m1) plt.plot(Kr_2, Ki_2, label=' m=%s'%m) plt.plot(Kr_3, Ki_3, label=' m=0') plt.xlabel(" - Ki") plt.ylabel(" - Kr") plt.legend(loc='best') plt.grid(True) alfa=1.2 Ki_1=[Ki(alfa,0.221,w) for w in n] Kr_1=[Kr(alfa,0.221,w) for w in n] Ki_2=[Ki(alfa,0.366,w) for w in n] Kr_2=[Kr(alfa,0.366,w) for w in n] Ki_3=[Ki(alfa,0,w) for w in n] Kr_3=[Kr(alfa,0,w) for w in n] plt.figure() plt.title(" \n alfa=%s"%alfa) plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)]) plt.plot(Kr_1, Ki_1, label=' m=%s'%m1) plt.plot(Kr_2, Ki_2, label=' m=%s'%m) plt.plot(Kr_3, Ki_3, label=' m=0') plt.xlabel(" - Ki") plt.ylabel(" - Kr") plt.legend(loc='best') plt.grid(True) plt.figure(
)
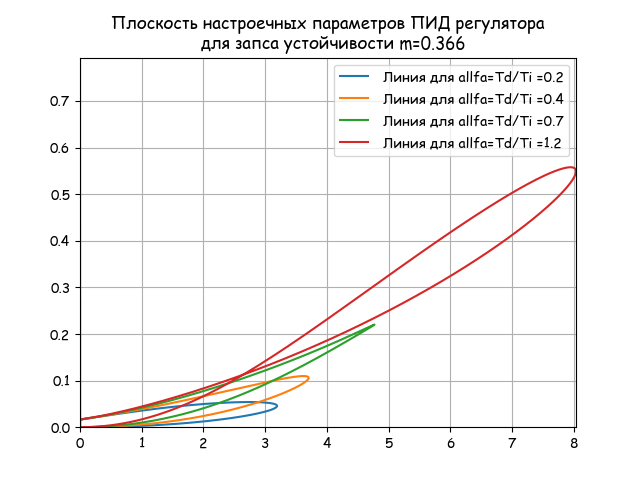
アルファ値–0.2,0,4,0,0.7の安定余裕m = 0.386の場合、Dパーティションを作成してアルファの臨界値を決定します。
すべてのチューニングパラメーターの共通面
plt.title(" \n m=%s"%m) alfa=0.2 Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] plt.plot(Kr_2, Ki_2,label=' allfa=Td/Ti =%s'%alfa) alfa=0.4 Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] plt.plot(Kr_2, Ki_2,label=' allfa=Td/Ti =%s'%alfa) alfa=0.7 Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] plt.plot(Kr_2, Ki_2,label=' allfa=Td/Ti =%s'%alfa) alfa=1.2 Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] plt.plot(Kr_2, Ki_2,label=' allfa=Td/Ti =%s'%alfa) plt.axis([0.0, round(max(Kr_2),3), 0.0, round(max(Ki_2),3)]) plt.legend(loc='best') plt.grid(True)
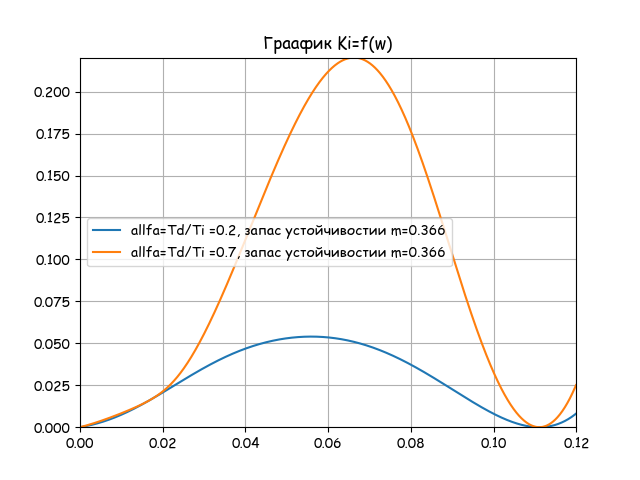
前のグラフで見つかった2つのアルファ値について、Kiの周波数wへの依存性をプロットします。0.2; 0.7。 Kiの設定は、共振周波数によって決まります。
plt.figure() plt.title(" Ki=f(w)") Ki_1=[Ki(0.2,m,w) for w in n1] Ki_2=[Ki(0.7,m,w) for w in n1] Ky=max([round(max(Ki_1),4),round(max(Ki_2),4)]) plt.axis([0.0,round(max(n1),4),0.0, Ky]) plt.plot(n1, Ki_1,label='allfa=Td/Ti =0.2, m=0.366') plt.plot(n1, Ki_2,label='allfa=Td/Ti =0.7, m=0.366') plt.legend(loc='best') plt.grid(True)
PIDコントローラーの3つの設定を決定します。
提案された基準に従って最適な設定を選択するための設定の数値の取得
maxKi=max( [Ki(0.7,m,w) for w in n1]) wa=round([w for w in n1 if Ki(0.7,m,w)==maxKi][0],3) Ki1=round(Ki(0.7,m,wa),3) Kr1=round(Kr(0.7,m,wa),3) Ti1=round(Kr1/Ki1,3) Td1=round(0.7*Ti1,3) d=[] d[0]= " №1 (wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr1,Ti1,Ki1,Td1) print(d[0]) maxKi=max( [Ki(0.2,m,w) for w in n1]) wa=round([w for w in n1 if Ki(0.2,m,w)==maxKi][0],3) Ki2=round(Ki(0.2,m,wa),3) Kr2=round(Kr(0.2,m,wa),3) Ti2=round(Kr2/Ki2,3) Td2=round(0.2*Ti2,3) d[1]= " №2 (wa =%s,m=0.366,alfa=0.2): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr2,Ti2,Ki2,Td2) print(d[1]) wa=fsolve(lambda w:Ki(0.7,m,w)-0.14,0.07)[0] wa=round(wa,3) Ki3=round(Ki(0.7,m,wa),3) Kr3=round(Kr(0.7,m,wa),3) Ti3=round(Kr3/Ki3,3) Td3=round(0.7*Ti3,3) d[2]= (" №3 (wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr3,Ti3,Ki3,Td3) print(d[2]) def Wsys(w,Kr,Ti,Td): j=(-1)**0.5 return (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td))) Wsys_1=[abs(Wsys(w,Kr1,Ti1,Td1)) for w in n2] Wsys_2=[abs(Wsys(w,Kr2,Ti2,Td2)) for w in n2] Wsys_3=[abs(Wsys(w,Kr3,Ti3,Td3)) for w in n2] plt.figure()
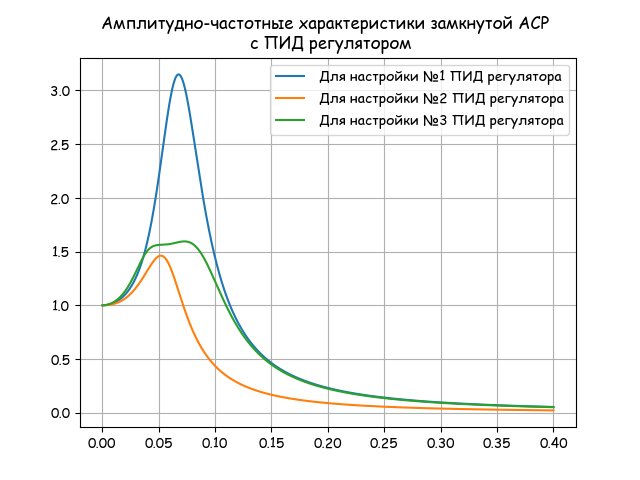
振動の周波数インジケーターの値によってASRのダイナミクスを決定します。
plt.title("- \n ") plt.plot(n2, Wsys_1,label=' №1 ') plt.plot(n2, Wsys_2,label=' №2 ') plt.plot(n2, Wsys_3,label=' №3 ') plt.legend(loc='best') plt.grid(True)
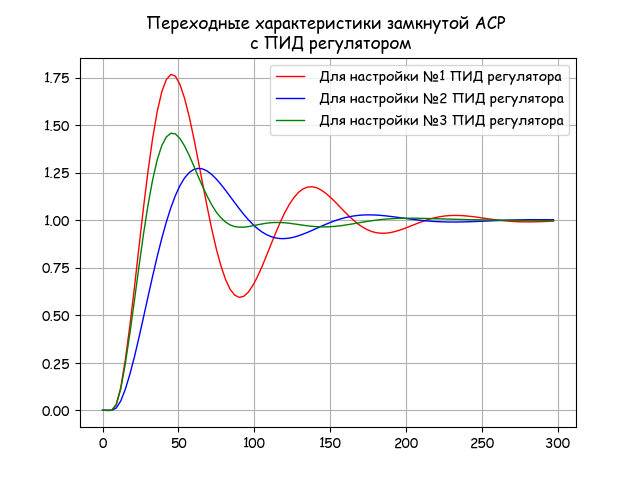
規制の質について提案されている積分基準に従って、最適なコントローラー設定を決定します。

受信した設定の最適性の数値およびグラフ分析
def ReWsys(w,t,Kr,Ti,Td): return(2/np.pi)* (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td))).real*(np.sin(w*t)/w) def h(t,Kr,Ti,Td): return quad(lambda w: ReWsys(w,t,Kr,Ti,Td),0,0.6)[0] tt=np.arange(0,300,3) h1=[h(t,Kr1,Ti1,Td1) for t in tt] h2=[h(t,Kr2,Ti2,Td2) for t in tt] h3=[h(t,Kr3,Ti3,Td3) for t in tt] I1=round(quad(lambda t: h(t,Kr1,Ti1,Td1), 0,200)[0],3) I11=round(quad(lambda t: h(t,Kr1,Ti1,Td1)**2,0, 200)[0],3) I2=round(quad(lambda t: h(t,Kr2,Ti2,Td2), 0,200)[0],3) I21=round(quad(lambda t: h(t,Kr2,Ti2,Td2)**2,0, 200)[0],3) I3=round(quad(lambda t: h(t,Kr3,Ti3,Td3), 0,200)[0],3) I31=round(quad(lambda t: h(t,Kr3,Ti3,Td3)**2,0, 200)[0],3) print(" I1 =%s ( №1)"%I1) print(" I2 =%s ( №1"%I11) print(" I1 =%s ( №2 )"%I2) print(" I2 =%s ( №2)"%I21) print(" I1 =%s ( №3 )"%I3) print(" I2 =%s ( №3)"%I31) Rez=[I1+I11,I2+I21,I3+I31] In=Rez.index(min(Rez)) print(" :\n %s"%d[In]) plt.figure() plt.title(" \n ") plt.plot(tt,h1,'r',linewidth=1,label=' №1 ') plt.plot(tt,h2,'b',linewidth=1,label=' №2 ') plt.plot(tt,h3,'g',linewidth=1,label=' №3 ') plt.legend(loc='best') plt.grid(True) plt.show()
プログラムの結果-テキスト出力:
PIDコントローラーの設定番号1(wa = 0.066、m = 0.366、alfa = 0.7):Kr = 4.77; Ti = 21.682; Ki = 0.22; Td = 15.177
PIDコントローラーの設定番号2(wa = 0.056、m = 0.366、アルファ= 0.2):Kr = 2.747; Ti = 50.87; Ki = 0.054; Td = 10.174
PIDコントローラーの設定番号3(wa = 0.085、m = 0.366、アルファ= 0.7):Kr = 3.747; Ti = 26.387; Ki = 0.142; Td = 18.471
線形積分品質基準I1 = 194.65(設定番号1)
二次積分品質基準I2 = 222.428(設定番号1
線形積分品質基準I1 = 179.647(設定番号2)
二次積分品質基準I2 = 183.35(設定番号2)
線形積分品質基準I1 = 191.911(設定番号3)
二次積分品質基準I2 = 204.766(設定番号3)
積分基準による最適パラメーター:
PIDコントローラーの設定番号2(wa = 0.056、m = 0.366、アルファ= 0.2):Kr = 2.747; Ti = 50.87; Ki = 0.054; Td = 10.174
プログラムの結果、グラフィック出力:



プログラムの全文
# -*- coding: utf8 -*- import numpy as np from scipy.integrate import quad from scipy.optimize import * import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' T1=14;T2=18;T3=28;K=0.9;tau=6.4# , , m=0.366;m1=0.221# n= np.arange(0.001,0.15,0.0002)# Kr-Ki n1=np.arange(0.00001,0.12,0.0001)# Ki=f(w) n2=np.arange(0.0002,0.4,0.0001)# def WO(m,w):# j=(-1)**0.5 return K*np.exp(-tau*(-m+j)*w)/((T1*(-m+j)*w+1)*(T2*(-m+j)*w+1)*(T3*(-m+j)*w+1)) def WR(w,Kr,Ti,Td):# j=(-1)**0.5 return Kr*(1+1/(j*w*Ti)+j*w*Td) def ReW(m,w):# j=(-1)**0.5 return WO(m,w).real def ImW(m,w):# j=(-1)**0.5 return WO(m,w).imag def A0(m,w):# return -(ImW(m,w)*m/(w+w*m**2)+ReW(m,w)/(w+w*m**2)) def Ti(alfa,m,w):# return (-ImW(m,w)-(ImW(m,w)**2-4*((ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m)*A0(m,w)))**0.5)/(2*(ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m)) def Ki(alfa,m,w):# return 1/(w*Ti(alfa,m,w)**2*alfa*(m*ReW(m,w)+ImW(m,w))-Ti(alfa,m,w)*ReW(m,w)+(m*ReW(m,w)-ImW(m,w))/(w+w*m**2)) def Kr(alfa,m,w):# if Ki(alfa,m,w)*Ti(alfa,m,w)<0: z=0 else: z=Ki(alfa,m,w)*Ti(alfa,m,w) return z def Kd(alfa,m,w):# return alfa*Kr(alfa,m,w)*Ti(alfa,m,w) alfa=0.2 Ki_1=[Ki(alfa,m1,w) for w in n] Kr_1=[Kr(alfa,m1,w) for w in n] Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] Ki_3=[Ki(alfa,0,w) for w in n] Kr_3=[Kr(alfa,0,w) for w in n] plt.figure() plt.title(" \n alfa=%s"%alfa) plt.axis([0.0, round(max(Kr_3),4), 0.0, round(max(Ki_3),4)]) plt.plot(Kr_1, Ki_1, label=' m=%s'%m1) plt.plot(Kr_2, Ki_2, label=' m=%s'%m) plt.plot(Kr_3, Ki_3, label=' m=0') plt.xlabel(" - Ki") plt.ylabel(" - Kr") plt.legend(loc='best') plt.grid(True) alfa=0.7 Ki_1=[Ki(alfa,0.221,w) for w in n] Kr_1=[Kr(alfa,0.221,w) for w in n] Ki_2=[Ki(alfa,0.366,w) for w in n] Kr_2=[Kr(alfa,0.366,w) for w in n] Ki_3=[Ki(alfa,0,w) for w in n] Kr_3=[Kr(alfa,0,w) for w in n] plt.figure() plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)]) plt.title(" \n alfa=%s"%alfa) plt.plot(Kr_1, Ki_1, label=' m=%s'%m1) plt.plot(Kr_2, Ki_2, label=' m=%s'%m) plt.plot(Kr_3, Ki_3, label=' m=0') plt.xlabel(" - Ki") plt.ylabel(" - Kr") plt.legend(loc='best') plt.grid(True) alfa=1.2 Ki_1=[Ki(alfa,0.221,w) for w in n] Kr_1=[Kr(alfa,0.221,w) for w in n] Ki_2=[Ki(alfa,0.366,w) for w in n] Kr_2=[Kr(alfa,0.366,w) for w in n] Ki_3=[Ki(alfa,0,w) for w in n] Kr_3=[Kr(alfa,0,w) for w in n] plt.figure() plt.title(" \n alfa=%s"%alfa) plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)]) plt.plot(Kr_1, Ki_1, label=' m=%s'%m1) plt.plot(Kr_2, Ki_2, label=' m=%s'%m) plt.plot(Kr_3, Ki_3, label=' m=0') plt.xlabel(" - Ki") plt.ylabel(" - Kr") plt.legend(loc='best') plt.grid(True) plt.figure() plt.title(" \n m=%s"%m) alfa=0.2 Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] plt.plot(Kr_2, Ki_2,label=' allfa=Td/Ti =%s'%alfa) alfa=0.4 Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] plt.plot(Kr_2, Ki_2,label=' allfa=Td/Ti =%s'%alfa) alfa=0.7 Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] plt.plot(Kr_2, Ki_2,label=' allfa=Td/Ti =%s'%alfa) alfa=1.2 Ki_2=[Ki(alfa,m,w) for w in n] Kr_2=[Kr(alfa,m,w) for w in n] plt.plot(Kr_2, Ki_2,label=' allfa=Td/Ti =%s'%alfa) plt.axis([0.0, round(max(Kr_2),3), 0.0, round(max(Ki_2),3)]) plt.legend(loc='best') plt.grid(True) plt.figure() plt.title(" Ki=f(w)") Ki_1=[Ki(0.2,m,w) for w in n1] Ki_2=[Ki(0.7,m,w) for w in n1] Ky=max([round(max(Ki_1),4),round(max(Ki_2),4)]) plt.axis([0.0,round(max(n1),4),0.0, Ky]) plt.plot(n1, Ki_1,label='allfa=Td/Ti =0.2, m=0.366') plt.plot(n1, Ki_2,label='allfa=Td/Ti =0.7, m=0.366') plt.legend(loc='best') plt.grid(True) maxKi=max( [Ki(0.7,m,w) for w in n1]) wa=round([w for w in n1 if Ki(0.7,m,w)==maxKi][0],3) Ki1=round(Ki(0.7,m,wa),3) Kr1=round(Kr(0.7,m,wa),3) Ti1=round(Kr1/Ki1,3) Td1=round(0.7*Ti1,3) d={} d[0]= " №1 (wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr1,Ti1,Ki1,Td1) print(d[0]) maxKi=max( [Ki(0.2,m,w) for w in n1]) wa=round([w for w in n1 if Ki(0.2,m,w)==maxKi][0],3) Ki2=round(Ki(0.2,m,wa),3) Kr2=round(Kr(0.2,m,wa),3) Ti2=round(Kr2/Ki2,3) Td2=round(0.2*Ti2,3) d[1]= " №2 (wa =%s,m=0.366,alfa=0.2): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr2,Ti2,Ki2,Td2) print(d[1]) wa=fsolve(lambda w:Ki(0.7,m,w)-0.14,0.07)[0] wa=round(wa,3) Ki3=round(Ki(0.7,m,wa),3) Kr3=round(Kr(0.7,m,wa),3) Ti3=round(Kr3/Ki3,3) Td3=round(0.7*Ti3,3) d[2]= " №3 (wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr3,Ti3,Ki3,Td3) print(d[2]) def Wsys(w,Kr,Ti,Td): j=(-1)**0.5 return (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td))) Wsys_1=[abs(Wsys(w,Kr1,Ti1,Td1)) for w in n2] Wsys_2=[abs(Wsys(w,Kr2,Ti2,Td2)) for w in n2] Wsys_3=[abs(Wsys(w,Kr3,Ti3,Td3)) for w in n2] plt.figure() plt.title("- \n ") plt.plot(n2, Wsys_1,label=' №1 ') plt.plot(n2, Wsys_2,label=' №2 ') plt.plot(n2, Wsys_3,label=' №3 ') plt.legend(loc='best') plt.grid(True) def ReWsys(w,t,Kr,Ti,Td): return(2/np.pi)* (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td))).real*(np.sin(w*t)/w) def h(t,Kr,Ti,Td): return quad(lambda w: ReWsys(w,t,Kr,Ti,Td),0,0.6)[0] tt=np.arange(0,300,3) h1=[h(t,Kr1,Ti1,Td1) for t in tt] h2=[h(t,Kr2,Ti2,Td2) for t in tt] h3=[h(t,Kr3,Ti3,Td3) for t in tt] I1=round(quad(lambda t: h(t,Kr1,Ti1,Td1), 0,200)[0],3) I11=round(quad(lambda t: h(t,Kr1,Ti1,Td1)**2,0, 200)[0],3) I2=round(quad(lambda t: h(t,Kr2,Ti2,Td2), 0,200)[0],3) I21=round(quad(lambda t: h(t,Kr2,Ti2,Td2)**2,0, 200)[0],3) I3=round(quad(lambda t: h(t,Kr3,Ti3,Td3), 0,200)[0],3) I31=round(quad(lambda t: h(t,Kr3,Ti3,Td3)**2,0, 200)[0],3) print(" I1 =%s ( №1)"%I1) print(" I2 =%s ( №1"%I11) print(" I1 =%s ( №2 )"%I2) print(" I2 =%s ( №2)"%I21) print(" I1 =%s ( №3 )"%I3) print(" I2 =%s ( №3)"%I31) Rez=[I1+I11,I2+I21,I3+I31] In=Rez.index(min(Rez)) print(" :\n %s"%d[In]) plt.figure() plt.title(" \n ") plt.plot(tt,h1,'r',linewidth=1,label=' №1 ') plt.plot(tt,h2,'b',linewidth=1,label=' №2 ') plt.plot(tt,h3,'g',linewidth=1,label=' №3 ') plt.legend(loc='best') plt.grid(True) plt.show()
結論
ソフトウェアは、線形および二次表現の利点を組み合わせた積分基準を使用して、PIDコントローラーの最適な設定を決定するための検索方法の完全な実装のために開発されました。