特定のプロパティを設定できるようにしながら、テスト多極関数を簡単に構築できるいくつかの方法を検討してください:Feldbaumメソッド、双曲線ポテンシャルに基づく関数、指数ポテンシャルに基づく関数。 これらの方法に加えて、高調波マルチエクストリーム関数とそれらのさまざまな組み合わせがあります。
フェルドバウム法
この方法は、次の形式の単純な累乗単一極値関数に基づいています。
$$表示$$ I_i(x-c_i)= \ sum_ {j = 1} ^ n a_ {ij} | x_j-c_ {ij} | ^ {p_ {ij}} + b_i、p_ {ij}> 0 $ $ディスプレイ$$
上記の関数は、ある点で最小値を持ちます $インライン$ c_i $インライン$ 、この時点での値は等しくなります $インライン$ b_i $インライン$ 。
もし $インライン$ p_ {ij}> 0 $インライン$ (極値の領域における関数の滑らかさの程度)、最小点で関数は滑らかになり、 $インライン$ 0 <p_ {ij} \ le1 $インライン$ 、最小点で関数は角度付きになります(微分できません)。
係数 $インライン$ a $インライン$ 極値領域での関数のクールさの度合いを担当します。
複数の極値関数を作成するには、1つの極値関数のセットに最小演算子を適用する必要があります。 一般的なビューは次のとおりです。
$$ display $$ I(x)= min \ {\ sum_ {j = 1} ^ m a_ {ij} | x_j-c_ {ij} | ^ {p_ {ij}} + b_i、i = \オーバーライン{1 、N} \} $$表示$$
例:
$$表示$$ I_1(x-c_1)= 7 | x_1 | ^ 2 + 7 | x_2 | ^ 2、$$表示$$
$$表示$$ I_2(x-c_2)= 5 | x_1 + 2 | ^ {0.5} +5 | x_2 | ^ {0.5} +6、$$表示$$
$$表示$$ I_3(x-c_3)= 5 | x_1 | ^ {1.3} +5 | x_2 + 2 | ^ {1.3} +5、$$表示$$
$$表示$$ I_4(x-c_4)= 5 | x_1 | ^ {1} +5 | x_2-4 | ^ {1} +8、$$表示$$
$$表示$$ I_5(x-c_5)= 4 | x_1-2 | ^ {1.5} +4 | x_2-2 | ^ {1.5} +7、$$表示$$
$$表示$$ I_6(x-c_6)= 5 | x_1-4 | ^ {1.8} +5 | x_2 | ^ {1.8} +9、$$表示$$
$$表示$$ I_7(x-c_7)= 6 | x_1-4 | ^ {0.6} +6 | x_2-4 | ^ {0.6} +4、$$表示$$
$$表示$$ I_8(x-c_8)= 6 | x_1 + 4 | ^ {0.6} +6 | x_2-4 | ^ {1.6} +3、$$表示$$
$$表示$$ I_9(x-c_9)= 3 | x_1 + 4 | ^ {1.2} +3 | x_2 + 4 | ^ {0.5} +7.5、$$表示$$
$$表示$$ I_ {10}(x-c_ {10})= 2 | x_1-3 | ^ {0.9} +4 | x_2 + 5 | ^ {0.3} +8.5、$$表示$$
$$ display $$ I(x)= min \ {I_i(x-c_i)、i = \ overline {1、N} \}。$$ display $$
指定された関数の等しいレベルの線のグラフは次のようになります。

スライス機能 $インライン$ x_1 = x_2 $インライン$ :
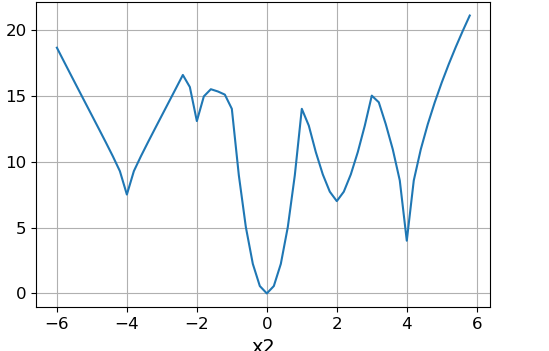
スライス機能 $インライン$ x_2 = 4 $インライン$ :
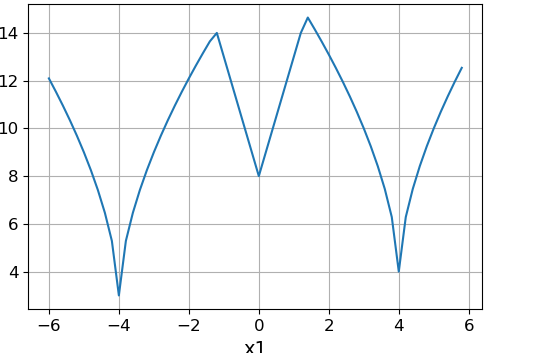
上記の関数は、ポイントで最小値を持ちます:(0、0)、(-2、0)、(0、-2)、(0、4)、(2、2)、(4、0)、(4、4 )、(-4、4)、(-4、-4)、(3、-5)。 グローバルはポイント(0、0)での最小値です。
テスト関数を生成するためのコード:
def get_test_function_method_min(n: int, a: List[List[float]], c: List[List[float]], p: List[List[float]], b: List[float]): """ :param n: :param a: , , / :param c: :param p: :param b: :return: , , """ def func(x): l = [] for i in range(n): res = 0 for j in range(len(x)): res = res + a[i][j] * np.abs(x[j] - c[i][j]) ** p[i][j] res = res + b[i] l.append(res) res = np.array(l) return np.min(res) return func
双曲線ポテンシャル関数
1つの極値関数の形式は次のとおりです。
$$表示$$ I_ {D、i}(x-c_i)=-\ frac {1} {b_i * \ sum_ {j = 1} ^ m a_ {ij} | x_j-c {ij} | ^ {p_ {ij}} + d_i}、b_i> 0、d_i> 0 $$表示$$
この関数には、ある点で最小値があります $インライン$ c_i $インライン$ 、その深さは $インライン$ d_i $インライン$ 。 勾配の程度は、係数を使用して設定されます $インライン$ b_i $インライン$ 、大きければ大きいほど極値領域は狭くなり、関数はより急勾配になります。
複数の極値関数を取得するには、加算演算子を適用する必要があります。
$$ディスプレイ$$ I(x)= \ sum_ {i = 1} ^ N I_ {D、i}(x-c_i)$$ディスプレイ$$
例:
$$表示$$ I_1(x-c_1)=-\ frac {1} {| x_1 + 4 | ^ 1 + | x_2 | ^ 1 + 0.25}、$$表示$$
$$表示$$ I_2(x-c_2)=-\ frac {1} {2 | x_1 | ^ 1 + 2 | x_2 | ^ 1 + 0.2}、$$表示$$
$$表示$$ I_3(x-c_3)=-\ frac {1} {0.5 | x_1 + 3 | ^ {0.6} +0.5 | x_2-3 | ^ {0.6} +0.1}、$$表示$$
$$表示$$ I_4(x-c_4)=-\ frac {1} {1.5 | x_1-2 | ^ 1 + 1.5 | x_2-2 | ^ 1 + 0.3}、$$表示$$
$$表示$$ I_5(x-c_5)=-\ frac {1} {0.8 | x_1 + 3 | ^ 1 + 0.8 | x_2 + 4 | ^ 1 + 0.35}、$$表示$$
$$表示$$ I(x_1、x_2)= \ sum_ {i = 1} ^ 5 I_ {D、i}(x-c_i)$$表示$$
指定された関数の等しいレベルの線のグラフは次のようになります。
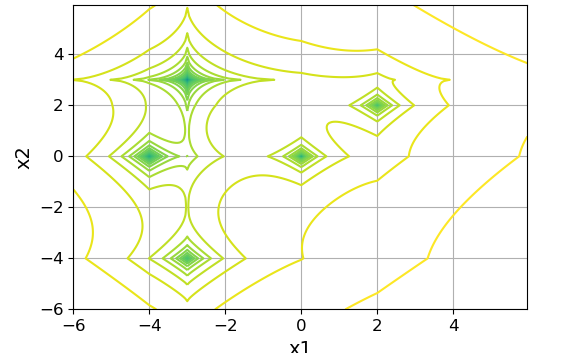
スライス機能 $インライン$ x_1 = x_2 $インライン$ :
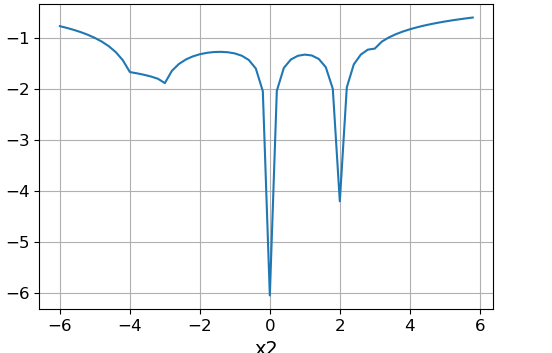
スライス機能 $インライン$ x_2 = x_1 + 3 $インライン$ :
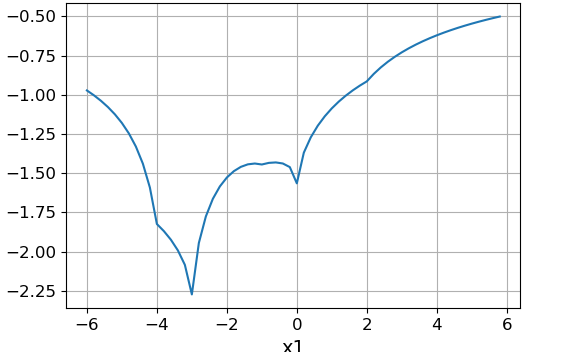
上記の関数は、ポイント(-4、0)、(0、0)、(-3、3)、(2、2)、(-3、-4)に最小値を持ちます。 グローバルは、ポイント(-3、3)の最小値です。
ネタバレの下に、分母に加法モジュラー関数を持つテスト関数を生成するためのコードがあります。
def get_tf_hyperbolic_potential_abs(n: int, a: List[float], c: List[List[float]], p: List[List[float]], b: List[float]): """ :param n: :param a: , :param c: :param p: :param b: , """ def func(x): value = 0 for i in range(n): res = 0 for j in range(len(x)): res = res + np.abs(x[j] - c[i][j]) ** p[i][j] res = a[i] * res + b[i] res = -(1 / res) value = value + res return value return func
指数ポテンシャル関数
1つの極値関数の形式は次のとおりです。
$$表示$$ I_ {E、i}(x-c_i)=-d_i * exp \ {-b_i * \ sum_ {j = 1} ^ m a_ {ij} | x_j-c_ {ij} | ^ {p_ {ij}} \}、b_i> 0、d_i> 0 $$表示$$
ここで、すべての文字の指定は、前の方法と同じ意味を持ちます。
複数の極値関数を取得するには、加算演算子も使用します。
$$表示$$ I(x)= \ sum_ {i = 1} ^ N I_ {U、i}(x-c_i)$$表示$$
例:
$$ディスプレイ$$ I_ {U、1}(x-c_1)=-6 * exp \ {-1 * [| x_1 + 4 | ^ {0.3} + | x_2 | ^ 1] \}、$$ディスプレイ$ $
$$ display $$ I_ {E、2}(x-c_2)=-5 * exp \ {-2 * [| x_1 | ^ {1} + | x_2 | ^ 1] \}、$$ display $$
$$ディスプレイ$$ I_ {U、3}(x-c_3)=-7 * exp \ {-0.5 * [| x_1 + 3 | ^ {0.6} + | x_2-3 | ^ {1.1}] \} $$表示$$
$$ディスプレイ$$ I_ {E、4}(x-c_4)=-4 * exp \ {-1.5 * [| x_1-2 | ^ {1.3} + | x_2-2 | ^ {0.8}] \} $$表示$$
$$表示$$ I_ {E、5}(x-c_5)=-4.5 * exp \ {-0.8 * [| x_1 + 3 | ^ {1.5} + | x_2 + 4 | ^ 2] \}、$$表示$$
$$表示$$ I(x_1、x_2)= \ sum_ {i = 1} ^ 5 I_ {Uh、i}(x-c_i)$$表示$$
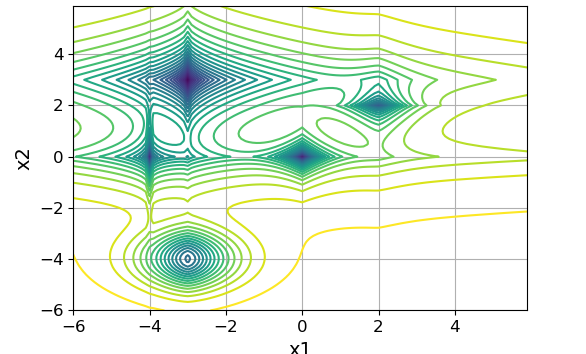
等しいレベルの線のグラフを以下に示します。
スライス機能 $インライン$ x_1 = x_2 $インライン$ :

スライス機能 $インライン$ x_2 = -x_1 $インライン$ :
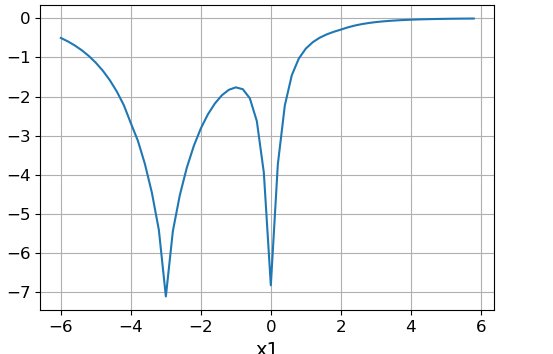
上記の関数は、ポイント(-4、0)、(0、0)、(-3、3)、(2、2)、(-3、-4)に最小値を持ちます。 グローバルは、ポイント(-3、3)の最小値です。
def get_tf_exponential_potential(n: int, a: List[float], c: List[List[float]], p: List[List[float]], b: List[float]): """ :param n: :param a: , :param c: :param p: :param b: """ def func(x): value = 0 for i in range(n): res = 0 for j in range(len(x)): res = res + np.abs(x[j] - c[i][j]) ** p[i][j] res = (-b[i]) * np.exp((-a[i]) * res) value = value + res return value return func
上記の方法に加えて、調和関数を使用できますが、その構成はより複雑なプロセスです。 そして主な欠点は、すべてのローカル低を制御できないことです。 これらのすべてのメソッドを組み合わせて、さらに複雑な機能を取得することもできます。
参照資料
Ruban A. I.多極関数の構築
ウィキペディア 最適化のためのテスト関数