ハスケル。 賢者と帽子の問題

三人の賢者は、どちらが最も賢いのかを議論しました。 真実を見つけるために、それぞれが彼の頭にランダムな色の帽子をかぶせました。 各セージは、相手の帽子の色を見ますが、自分の帽子の色は見ません。 勝者は彼の帽子の色を決定できる人です。



そのため、3つすべてが白いキャップを引き出しました。 通りすがりの通行人は、「あなたの一人が白い帽子をかぶっています」と言います。 しばらくして、賢い賢者たちは「白い帽子をかぶっています!!!」と叫びました。



彼はこれについてどう思いましたか？

私たちの賢者を正しい答えに導いた推論の特定のシーケンスがあります。 これらの考慮事項をモデル化しようとします。

彼はこれについてどう思いましたか？

このタスクは、任意の数の賢人向けに定式化できます。 最も単純なオプションを見てみましょう。



白い帽子をかぶった2人の賢者が座っています。 両方とも、少なくとも1つの白いキャップがあることを知っています。 そして、賢者の一人は次のように主張しています。 しかし、彼は沈黙しています。 白い帽子が私の上にある！」



3つの賢者がいるとき、そのうちの1人は次のように主張します。「私の帽子が白でない場合、2番目の賢者はそう思うでしょう。 ...（次は2人の賢者の問題からの推論です）...そのうちの1人は、白い帽子がかかっていると推測していました。 しかし、どちらも沈黙しています。 だから私の最初の推測は真実ではなく、私は白い帽子をかぶっています！」



帰納法により、この推論を任意の数の賢人に拡張できます。 さらにこの記事では、3人の賢者の状況をモデル化します。

タスクステートメント

元の定式化では、問題は完全に正しいわけではありません。 他の賢者が彼の帽子の色を推測しなかったと結論付けるためにどれくらいの時間を経過すべきかは明らかではありません。 問題をより正確に再定式化させてください。

3つの賢者がいます。 各キャップは黒または白です。 誰もが相手の色を知っていますが、自分の色を知りません。



初日には、少なくとも1つの白い帽子があることが通知されます。 彼らは一日中考え、一日の終わりに独立して投票します。 それらは、「私は自分の色を知っている」、「私は自分の色を知らない」という2つの可能な結果のうちの1つを与えます。



二日目に、彼らは各対戦相手の「投票結果」に精通します。 その後、彼らは一日中考え直し、一日の終わりに再び投票します。



などなど。



質問 異なる初期条件の下で、各セージは毎日どのように投票しますか？

コード

まず、作業に使用する主なタイプについて説明します。

data Color = Black | White deriving (Show, Eq) type State = [Color] fullState :: [State] fullState = do c1 <- [Black, White] c2 <- [Black, White] c3 <- [Black, White] return [c1, c2, c3] type StateInfo a = State -> a stateInfoColor :: Int -> StateInfo Color stateInfoColor i state = state !! i stateInfoAnyWhite :: StateInfo Bool stateInfoAnyWhite state = or $ map (\c -> c == White) state
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

（キャップ​​がオンになっている）世界の状態は、 Stateタイプを使用して記述されます。 fullState変数には、可能なすべての状態のリストを格納します。



StateInfoタイプは、世界の状態から計算できる情報を記述します。 たとえば、 stateInfoColorを使用して、特定のセージのキャップの色を分離できます。 また、 stateInfoAnyWhiteを使用して、特定の状態ですべてのキャップが白であるというステートメントが真であるかどうかを計算します。



次はより複雑な設計です。

 type Knowledge = State -> (State -> Bool) knowledgeAbout :: (Eq a) => StateInfo a -> Knowledge knowledgeAbout stateInfo state = let info = stateInfo state in \s -> stateInfo s == info knowledgeIsTrue :: StateInfo Bool -> Knowledge knowledgeIsTrue si _ state = si state knowledgeAboutColor1 :: Knowledge knowledgeAboutColor1 = knowledgeAbout $ stateInfoColor 0 knowledgeAboutColor2 :: Knowledge knowledgeAboutColor2 = knowledgeAbout $ stateInfoColor 1 knowledgeAboutColor3 :: Knowledge knowledgeAboutColor3 = knowledgeAbout $ stateInfoColor 2
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

知識の種類は、世界についての「知識」を表します。 後で見るように、 ナレッジタイプはStateInfoタイプとさまざまな方法で結合されます。 これは非常に重要なタイプです。 これについて詳しく説明します。



Knowledgeの定義からわかるように、これは世界の状態から何らかのフィルタリング関数を計算する関数です。 つまり 私たちは世界の「実際の」状態を送信し、私たちの知識に矛盾しない可能な状態のサブセットを提供します。



たとえば、 knowledgeAboutColor1関数は、最初のセージの色に関する知識を表します。 最初のセージの色が白である状態[White、Black、Black]を渡すと、最初のセージの色が異なるすべての状態を除外する関数を返します。



セージを指定する特別な構造はありません。 「知識」の観点から判断します。 そのような推論の例を次に示します。



= + + ,



= +









以下に、 KnowledgeとStateInfoの観点から見たヘルパー関数を示します。

 knowledgeAnd :: [Knowledge] -> Knowledge knowledgeAnd list stateTrue = \s -> and $ map (\f -> f stateTrue s) list stateInfoList :: [StateInfo a] -> StateInfo [a] stateInfoList sil state = map (\si-> si state) sil knowledgeImply :: Knowledge -> Knowledge -> StateInfo Bool knowledgeImply knowledge1 knowledge2 state = and $ map (\(b1, b2) -> not $ and [b1, not b2]) $ map (\s -> (knowledge1 state s, knowledge2 state s)) fullState
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

knowledgeAnd関数は、単に知識を1つに結合します。



stateInfoList関数のアクションは、そのタイプから明らかです。



3番目の機能は知識です。 これは、最初の知識から2番目の知識が続くという声明です。



次は、タスクに直接関係するコードです。

 type KnowledgeList = [(Knowledge, Knowledge)] insightList :: KnowledgeList -> StateInfo [Bool] insightList knowledgeList = stateInfoList $ map knowledgeInsight knowledgeList knowledgeInsight :: (Knowledge, Knowledge) -> StateInfo Bool knowledgeInsight (currentKnowledge, targetKnowledge) = knowledgeImply currentKnowledge targetKnowledge manStart_1 = knowledgeAnd [knowledgeAboutColor2, knowledgeAboutColor3, knowledgeAbout stateInfoAnyWhite] manStart_2 = knowledgeAnd [knowledgeAboutColor1, knowledgeAboutColor3, knowledgeAbout stateInfoAnyWhite] manStart_3 = knowledgeAnd [knowledgeAboutColor1, knowledgeAboutColor2, knowledgeAbout stateInfoAnyWhite] knowledgeList_1 :: KnowledgeList knowledgeList_1 = [(manStart_1, knowledgeAboutColor1), (manStart_2, knowledgeAboutColor2), (manStart_3, knowledgeAboutColor3)] insightList_1 :: StateInfo [Bool] insightList_1 = insightList knowledgeList_1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

KnowledgeListタイプは、賢者のリストのようなものです。 賢者ごとに、一対の知識があります。 最初の要素は彼の現在の知識です。 2番目の要素は、彼が把握しようとしているもの、つまり帽子の色です。



knowledgeInsight関数は、特定のセージが彼の色を判別できたかどうかを計算します。 言い換えれば、彼が求める知識は、彼が所有する知識から流れ出るのか。 魔法のknowledgeImply関数が使用されます。



変数manStart_1 、 manStart_2 、 manStart_3は、それぞれの賢者の初期知識です。



変数knowledgeList_1は、初日のすべての賢者のリストです（彼らの知識）。



変数insightList_1-これらは、初日の投票の結果です。



投票結果が得られたら、賢者の知識の新しいリストを作成できます。

 addNewKnowledge :: Knowledge -> KnowledgeList -> KnowledgeList addNewKnowledge newKnowledge knowledgeList = flip map knowledgeList $ \(oldKnowledge, targetKnowledge) -> (knowledgeAnd [oldKnowledge, newKnowledge], targetKnowledge) knowledgeList_2 :: KnowledgeList knowledgeList_2 = addNewKnowledge (knowledgeAbout insightList_1) knowledgeList_1 insightList_2 :: StateInfo [Bool] insightList_2 = insightList knowledgeList_2 knowledgeList_3 :: KnowledgeList knowledgeList_3 = addNewKnowledge (knowledgeAbout insightList_2) knowledgeList_2 insightList_3 :: StateInfo [Bool] insightList_3 = insightList knowledgeList_3
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

addNewKnowledge関数を使用して、すべての賢者を調べ、それらに新しい知識を追加します（前日の投票の結果）。



手順を数回繰り返して、変数insightList_1 、 insightList_2 、およびinsightList_3を取得します-3日間の投票の結果。



最後に、特定の初期状態の結果を表示します。

 startState = [White, White, White] main = do putStr $ "day 1 result: " ++ (show $ insightList_1 startState) ++ "\n" putStr $ "day 2 result: " ++ (show $ insightList_2 startState) ++ "\n" putStr $ "day 3 result: " ++ (show $ insightList_3 startState) ++ "\n"
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果

まず、すべてのキャップが白の場合、最も難しくて興味深いオプションを検討してください。

 startState = [White, White, White] {- result: day 1 result: [False,False,False] day 2 result: [False,False,False] day 3 result: [True,True,True] -}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

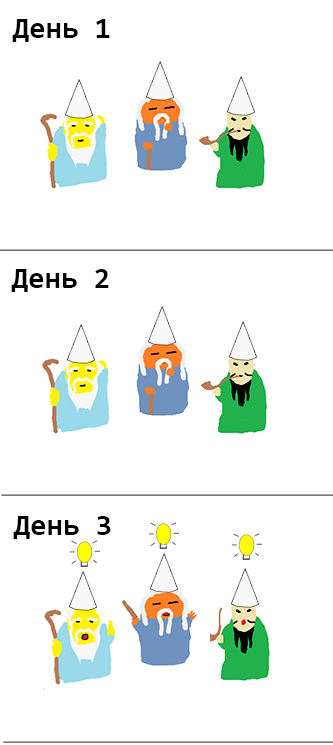
最初の2日間で、賢者は考えました。 そして3日目に、3人は自分の色を知っていると宣言しました。



残念ながら、「賢い」人を特定することはできませんでした。 すべての賢者は可能な限り賢く、利用可能なすべての情報を最大限に活用すると仮定します。 彼らの推論では、他の賢者も可能な限り賢いという事実を使用しています。



キャップの1つが黒の場合はどうなりますか？

 startState = [Black, White, White] {- result: day 1 result: [False,False,False] day 2 result: [False,True,True] day 3 result: [True,True,True] -}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

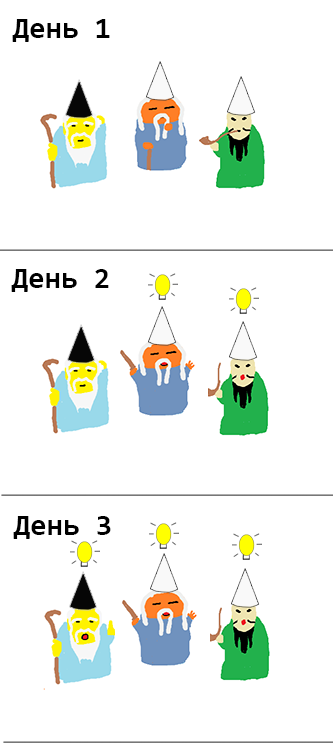
2日目にすでに白の2つのセージが色を決定できたことがわかります。 驚くことではありません。彼らにとっては、状況全体が二人の賢者の問題に帰着するからです。 彼らの反応を見て、残りの賢者は彼の色を決定することができました。



次に、2つの黒いキャップの例を示します。

 startState = [Black, Black, White] {- result: day 1 result: [False,False,True] day 2 result: [True,True,True] day 3 result: [True,True,True] -}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、初日の白い帽子のセージは彼の色を決定することができました。 そして、これは他の賢者に彼らが黒い帽子を持っているという明確なシグナルです。

おわりに

結果の例は、さらなる研究と実験のための良い出発点です。 それを使用すると、「彼は私が知っていることを知っていることを知っている..」というスタイルで他の問題を解決できます。



私のコードでは、セージと日数はハードコートされています。 明確にするために、NセージとN日間に一般化することは特に始めませんでした。 おそらく次の記事では、コマンドを使用して書き直します。