🙍 😹 🎷 線形動的システムの同定の周波数法：理論と実践 🖖🏽 ⏸️ 👩🏼‍🤝‍👨🏽

実際のTAUアプリケーションでは、制御オブジェクトを正確かつ正確に識別することが必要になることがよくあります。この記事では、周波数制御オブジェクトの識別に焦点を当てます。この方法は、広い範囲で周波数を変更することにより、正弦波入力の影響により制御オブジェクトを物理的にテストできる場合に適用できます。この条件が満たされている場合、結果として、原則として、最も楽観的な期待が正当化されます。

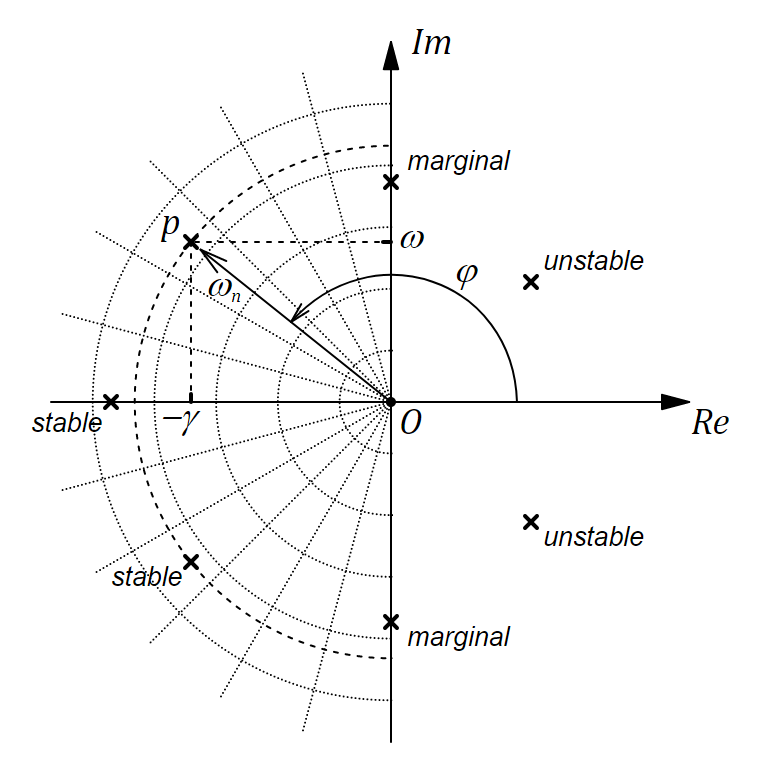
伝達関数の極

知っておくべきこと

簡単な理論的背景から始めましょう。記事の内容を理解するには、読者は次のことを理解している必要があります。

ラプラス変換
線形動的システム
特性方程式
伝達関数
離散フーリエ変換
ボード機能：LACHおよびLFCH

正弦波応答

ご存じのように、正弦波効果に対する動的システムの応答は、同じ周波数ですが優れた振幅と位相を持つ正弦波です。それは、これら2つの特性です。ボード線図を形成する振幅と位相、つまりLACHとLFCHです。実際、動的システムを識別するタスクは、これら2つのグラフの実験結果に限定されます。

例として、2次線形力学系の例として、右辺がゼロでない調和振動子の方程式を考えます

d d o t x （ t ） + 2 g a m m a d o t x （ t ） + o m e g a_{n}^{2} x （ t ） = u （ t ）

$\ ddot {x}（t）+ 2 \ gamma \ dot {x}（t）+ \ omega_n ^ 2 x（t）= u（t）$

任意の関数のラプラス変換を示します

f （ t ）

$f（t）$ を通して

h a t f （ s ） = m a t h c a l L l b r a c e f （ t ） r b r a c e

$\ hat {f}（s）= \ mathcal {L} \ lbrace f（t）\ rbrace$ 。ラプラス変換を方程式の両側に適用します

s^{2} \、 h a t x （ s ） + 2 g a m m a \、 s \、 h a t x （ s ） + o m e g a_{n}^{2} \、 h a t x （ s ） = h a t u （ s ）

$s ^ 2 \、\ hat {x}（s）+ 2 \ gamma \、s \、\ hat {x}（s）+ \ omega_n ^ 2 \、\ hat {x}（s）= \ hat { u}（s）$

そうすると、力学系の特性方程式は

l a m b d a^{2} + 2 g a m m a \、 l a m b d a + o m e g a_{n}^{2} = 0

$\ lambda ^ 2 + 2 \ gamma \、\ lambda + \ omega_n ^ 2 = 0$

伝達関数

H （ s ） = f r a c h a t x （ s ） h a t u （ s ） = f r a c 1 s^{2} + 2 g a m m a \、 s + o m e g a_{n}^{2}

$H（s）= \ frac {\ hat {x}（s）} {\ hat {u}（s）} = \ frac {1} {s ^ 2 + 2 \ gamma \、s + \ omega_n ^ 2}$

LACHおよびLPCHの望ましい特性は、

s \右 矢 印 j \オ メ ガ

$s \右矢印j \オメガ$ そして、モジュールと関数の引数を取ります

H （ j \オ メ ガ ）

$H（j \オメガ）$ それに応じて

b e g i n s p l i t a （ o m e g a ） ＆ = l e f t | H （ j o m e g a ） r i g h t | v a r p h i （ o m e g a ） ＆ = a r g H （ j o m e g a ） e n d s p l i t

$\ begin {split} a（\ omega）＆= \ left | H（j \ omega）\ right | \\ \ varphi（\ omega）＆= \ arg {H（j \ omega）} \ end {split}$

ここに

a （ \オ メ ガ ）

$a（\オメガ）$ -振幅（大きさ）、および

v a r p h i （ o m e g a ）

$\ varphi（\ omega）$ -周波数での対応するコンポーネントの位相（位相）

\オ メ ガ

$\オメガ$ 。結果はこれに似たものになります。

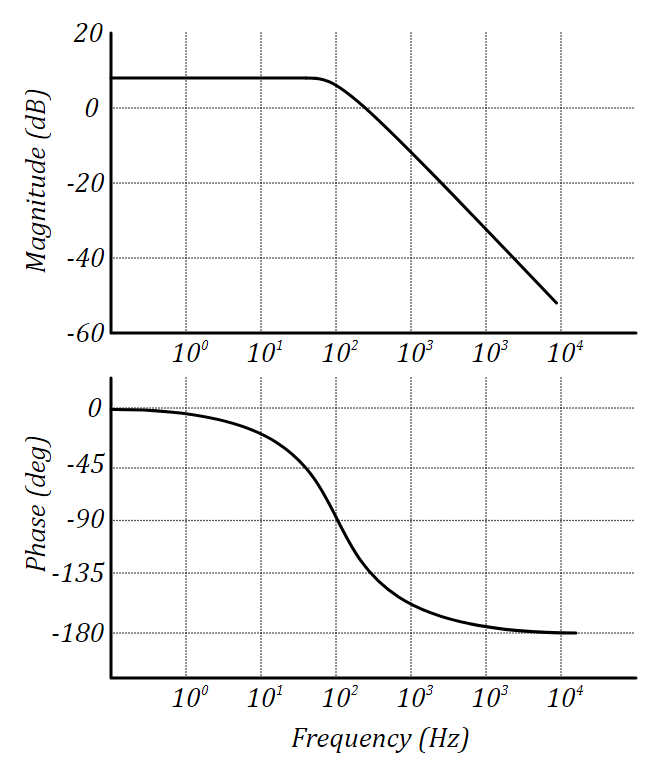
ボード機能：LACHおよびLFCH

これらの2つのグラフは、動的システムを一意に特徴付けます。逆もまた真であり、動的システムのLACHおよびLFC特性をある程度の精度で知っているため、このシステムをいくつかの信頼区間で完全に識別することができます。問題は、周波数応答を取得する方法です。これについては後で説明します。

入力に正弦波効果を適用することにより、次のようなものを観察します

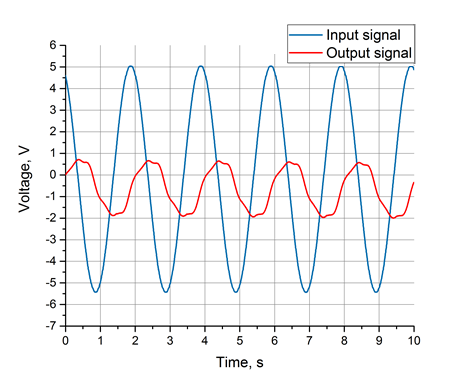
正弦波入力とシステム応答

グラフは実験で取得されます。グラフからわかるように、入力信号と同じ周波数の正弦波成分が出力信号に明確に存在します。ただし、これに加えて、高調波とノイズも高くなる場合があります。ただし、フーリエ変換は非常に優れた強力な分析ツールであるため、すべての外乱を除外して有用な信号を強調できるため、心配する必要はありません。

離散フーリエ変換

2つのグラフ、入力インパクトを測定したとしましょう

u （ t ）

$u（t）$ およびシステム応答

x （ t ）

$x（t）$ 、特定の入力露出周波数に対して

f

$f$ 。両方の測定は、同期して同じサンプリング周期で実行する必要があります。

T

$T$ 十分に正確に知られている必要があります。したがって、離散値の2つのセットがあります

u_{n} = u （ t_{n} ）

$u_n = u（t_n）$ そして

x_{n} = x （ t_{n} ）

$x_n = x（t_n）$ どこで

n = 0, 1 、 \ド ッ ト 、 N

$n = 0,1、\ドット、N$ 、そして

u_{n}

$u_n$ そして

x_{n}

$x_n$ -値

u （ t ）

$u（t）$ そして

x （ t ）

$x（t）$ 対応する個別の時点で

t_{n}

$t_n$ 。合計測定時間は、少なくとも数周期（3回以上を推奨）の振動を捕捉するのに十分な長さである必要があることに注意してください。

離散集合へ

l b r a c e u_{n} r b r a c e

$\ lbrace u_n \ rbrace$ そして

l b r a c e x_{n} r b r a c e

$\ lbrace x_n \ rbrace$ 離散フーリエ変換を適用できます。離散フーリエ変換は、上記の信号を時間領域から周波数領域に変換します。

b e g i n s p l i t l b r a c e u_{n} r b r a c e ＆ r i g h t a r r o w l b r a c e U_{k} r b r a c e l b r a c e x_{n} r b r a c e ＆ r i g h t a r r o w l b r a c e X_{k} r b r a c e e n d s p l i t

$\ begin {split} \ lbrace u_n \ rbrace＆\ rightarrow \ lbrace U_k \ rbrace \\ \ lbrace x_n \ rbrace＆\ rightarrow \ lbrace X_k \ rbrace \ end {split}$

どこで

k = 0, 1 、 \ド ッ ト 、 N / 2

$k = 0,1、\ドット、N / 2$ 、そして

U_{k}

$U_k$ そして

X_{k}

$X_k$ -対応する複素振幅

k

$k$ 高調波。

メソッド適用

次に、2つの信号に離散フーリエ変換を適用します。下の図は、振幅グラフを示しています。

| U_{k} |

$| U_k |$ そして

| X_{k} |

$| X_k |$

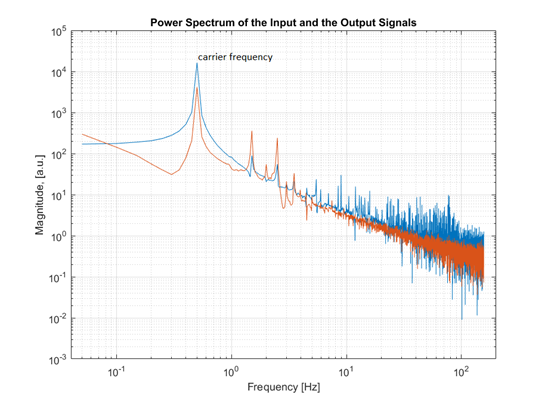
入力および出力信号の振幅スペクトル

グラフは、実験データを処理することでも取得されます。ご覧のように、周波数で鋭いピーク

f = 0.4

$f = 0.4$ Hz。これは、入力アクションの「キャリア」周波数、つまり制御オブジェクトが励起された周波数です。入力と出力の両方のグラフで、特定の高調波のピークが観察されます。複素振幅の2つの値のうち

U_{k}

$U_k$ そして

X_{k}

$X_k$ この周波数で、伝達関数の値を取得します

H_{k}

$H_k$ 。

覚えているように

H （ s ） = f r a c h a t x （ s ） h a t u （ s ）

$H（s）= \ frac {\ hat {x}（s）} {\ hat {u}（s）}$

離散の場合

u_{n}

$u_n$ そして

x_{n}

$x_n$ 私たちは持っています

H_{k} = f r a c X_{k} U_{k}

$H_k = \ frac {X_k} {U_k}$

次に、LACHおよびLFC曲線で、ポイントをプロットできます。

b e g i n s p l i t a_{k} ＆ = l e f t | H_{k} r i g h t | v a r p h i_{k} ＆ = a r g H_{k} e n d s p l i t

$\ begin {split} a_k＆= \ left | H_k \ right | \\ \ varphi_k＆= \ arg {H_k} \ end {split}$

数のある高調波にはどのような周波数がありますか？

k

$k$ ？私達は答えます：調和的な頻度は公式によって与えられます

f_{k} = f r a c k N T

$f_k = \ frac {k} {NT}$

記録することもできます

o m e g a_{k} = f r a c 2 p i k N T

$\ omega_k = \ frac {2 \ pi k} {NT}$

実際、高調波の表現は次のとおりです。

h_{k} （ t ） = a_{k} s i n l e f t （ o m e g a_{k} t + v a r p h i_{k} r i g h t ）

$h_k（t）= a_k \ sin \ left（\ omega_k t + \ varphi_k \ right）$

上記の手順は、周波数範囲全体をキャプチャするのに十分な回数繰り返す必要があります。原則として、低周波数と高周波数でより大きな周波数ステップを使用できます。逆に、中間周波数の領域、特に共振付近では、より細かいステップが必要です。

このような実験を行い、データを処理すると、周波数特性の表が得られます

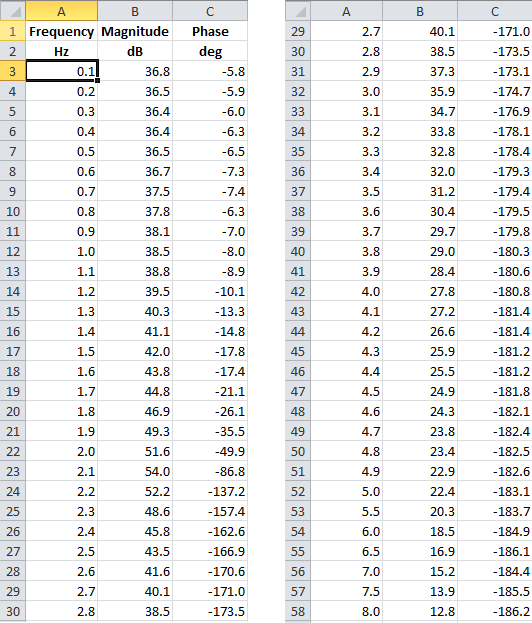
周波数応答表

LACHとLFCHの測定グラフをすぐに作成できます。こんな感じ

実験データに基づいて構築されたLACHおよびLPCH

離散メソッドを使用しましたが、これら2つのグラフは元の物理システム、つまり制御オブジェクトのダイナミクスを反映しており、離散化に関連する単純化は行われていません（もちろん、この周波数範囲で）。

次に、MATLAB、より具体的にはSystem Identification Toolboxを使用する必要があります。このツールボックスには、周波数データを使用してシステムを識別することができる対話型アプリケーションであるシステム識別アプリがあります。ところで、時間測定による直接識別など、他のオプションがあります。

正しい識別のために、システムの順序を知る必要があります。ここでは、LPFのスケジュールに助けられます。システムの次数を調べるには、LPF曲線を見て、高周波数での位相が90度遅れる回数を推定します。回数は90度で、システムの順序（分母）があります。

識別中に、レポートが自動的に生成されます。これは非常に便利です。こんな感じ

tf1 = From input "u1" to output "y1": -97.64 s + 1.063e04 --------------------- s^2 + 1.547 s + 176.7 Name: tf1 Continuous-time identified transfer function. Parameterization: Number of poles: 2 Number of zeros: 1 Number of free coefficients: 4 Use "tfdata", "getpvec", "getcov" for parameters and their uncertainties. Status: Estimated using TFEST on frequency response data "h". Fit to estimation data: 92.26% (stability enforced) FPE: 120.6, MSE: 112.3

識別レポートによると、入力データは見つかったモデルによって92.26％満たされています。物理システムの次の伝達関数があります

H （ s ） = f r a c - 97.64 \、 s + 1.063 t i m e s 10^{4} s^{2} + 1.547 \、 s + 176.7

$H（s）= \ frac {-97.64 \、s + 1.063 \ times10 ^ 4} {s ^ 2 + 1.547 \、s + 176.7}$

これで、tf1という名前のIDTF型のオブジェクトが作成されました。これを使用して、MATLABの他のLTIシステムと同じことができます。さらに、オブジェクトには内部パラメーターの不確実性に関する情報が含まれており、ボード線図を作成すると、チャート上で信頼区間を呼び出すことができます。設定では、標準偏差の数を指定できます。

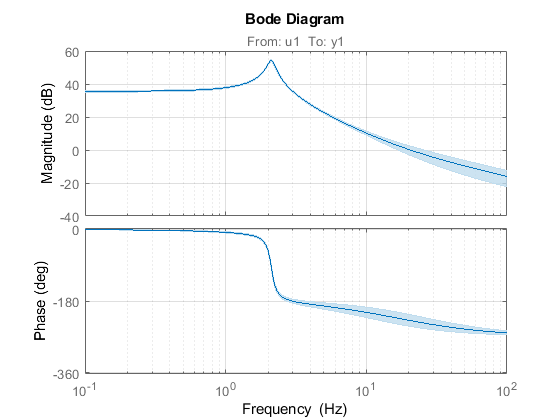
信頼区間をもつ識別されたシステムモデル

同定の正確性を検証するために、実験点を同定されたモデルの周波数特性のグラフと組み合わせることができます

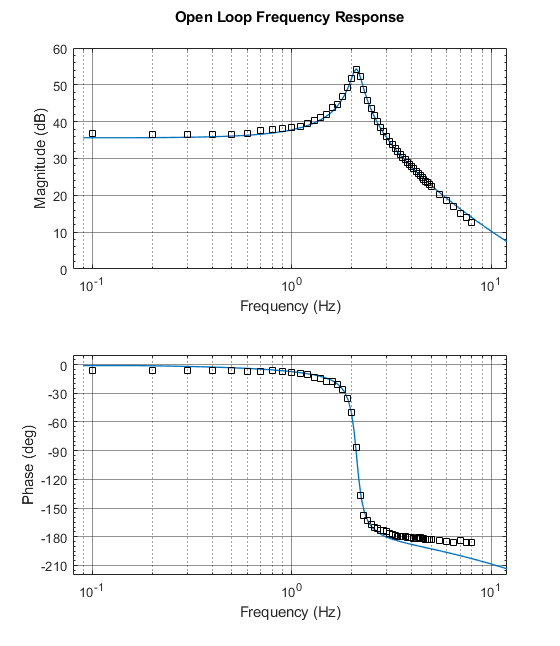
LACHとLFCHの組み合わせグラフ

おわりに

この方法を使用すると、制御システムの設計プロセスが大幅に容易になります。この記事の著者は、LQGに特殊用途の油圧回路用のコントローラーを開発して実装しました。さらに、この方法は、制御システムの有効性を評価するために使用できます。ただし、不要な外乱から制御オブジェクトへの入力の影響が物理的にアクセスできる場合に限ります。

線形動的システムの同定の周波数法：理論と実践

知っておくべきこと

正弦波応答

離散フーリエ変換

メソッド適用

おわりに

More articles: