距離の概念そのものが人工的なものであり、現実に固有のものではないことを想像してください。 距離のない世界を想像することはできますか? この記事では、いくつかの数学的概念、すなわち離散空間、シンプレックス、トーラスを使用してこれを行う1つの方法を提案しています。 これらの概念の議論から、多次元データの視覚化に関するいくつかの結論が導かれます。
ポイント間の距離が同じスペース
距離は、あるオブジェクトが他のオブジェクトからどれだけ近いか、または離れているかの尺度です。 おもちゃに手を伸ばそうとするとき、私たちは幼児期に距離のアイデアに出会います。 それから私たちは歩き始めて、私たちが今いる場所から遠く離れたオブジェクトに到達する能力を開発し始めます。 産業全体(輸送、郵便、通信)は、人や物を輸送したり情報を送信したりする必要がある一定の距離があるという事実に基づいて構築されています。 双眼鏡などのさまざまなデバイスは、少なくとも視覚的に距離を縮めることができます。
また、距離は間接的に使用できます。 データを視覚化するとき、ポイントと他のオブジェクト間の距離を使用して、他の値間の関係を示します。 計器では、「より近い」という考えは、「寒暖」(温度計の目盛り)、「軽く重い」(重量の目盛り)、「遅いほど速い」(速度計の目盛り)の類似物として機能します。 途中で、また変数の値を理解するために、彼自身のために距離を測定できます。
距離を考えるのは難しくありません。 さらに、これは自然な方法で取得されます。
数学では、距離は距離空間の概念に関連付けられています 。 距離空間の任意の2点(要素、オブジェクト)の間で、距離(距離)が定義されます。 メトリックは、より近い関係とより近い関係を定量的に表現したものです。つまり、どれだけ近いか、どれだけ遠いかという質問に答えます。 幾何学的および地理的に、メトリックは明らかな意味を持ち、キロメートル、マイルなどで表されます。 一般的な意味では、メトリックは、たとえば競争の参加者の評価など、あらゆる意味を持ちます。 この場合、メトリックは得点の数であり、開始点が最初の場所です。
これらの例はすべて、距離の概念が私たちの生活にとってどれほど重要であるかを示すために必要でした。 距離のない人生を想像できますか? インターネットの出現により、コミュニケーションの観点からはより簡単になりましたが、私たちの生活の他の多くの側面は依然として距離の概念と強く関連しています。 それにも関わらず、メトリックdが一定で、たとえばユニティに等しい数学的な抽象化を作成できます。 このような抽象化はすでに存在し、 離散空間 Xと呼ばれます :
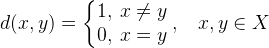
この定義では、 xとyは空間の2点(要素、オブジェクト)です。 定義は、すべてのポイントが互いに等しく遠くまたは等しく近いことを意味します。 どんな点でも、他の距離は同じであることがわかります。 点Aから点Bに移動するには、同じ時間かかります。 さらに、ポイントBでは状況は同じです-再び、他のポイントまでの距離はポイントAと同じになります。
離散空間は、カーアトラスで行われているように、 距離の表の形で簡単に想像できます。 このようなテーブルの行と列の交点には、テーブルのこの行と列に対応するポイントの距離が示されます。 定義によれば、このようなテーブルの対角線に沿った離散空間ではゼロが残り、他のすべての値は統一されます。 AからFまでの6点で構成されるスペースの例:

または都市(キロメートル単位)の場合:
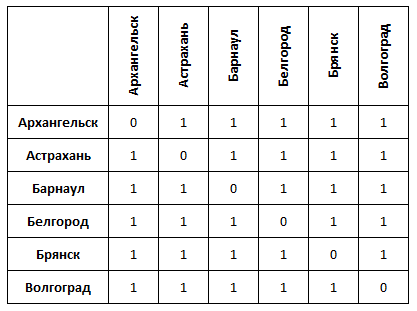
抽象点を含むマトリックスを想像するのは簡単ですが、特定の都市では、地理地図の安定したアイデアがあるため、すでにはるかに困難です。 ジオメトリの基本である距離と近距離関係の概念がない視覚化を作成するにはどうすればよいですか? ある点から開始し、他のすべての点から同じ距離に点を次々に追加して、離散的な空間を描いてみましょう。
シンプレックスを使用した離散空間の可視化
まず、離散空間が1つのポイントAのみで構成されていると想像してみましょう。たとえば、これはシステムのある状態かもしれません。 点は1つしかないため、システムは常に一定であり、常に点Aに対応する状態にあります。2次元平面上のこの点の画像は基本です(対応する距離の表は、離散空間の定義に従ってその隣に表示されます)。
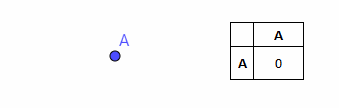
そのようなスペースでは、移動や変更はできません。 このようなスペースは、ある変数の定数値に対応していると言えます。
距離1で別のポイントを追加します。2つのポイントも平面に簡単に描画できます。 それらの間の距離とともに、セグメントABを形成します。
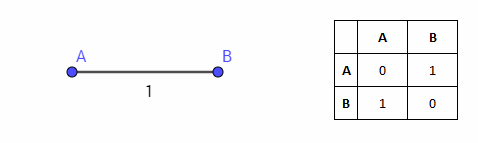
ここで、平面Cに別のポイントを描画してみましょう。ポイントAとBから1の距離に配置し、これらのポイント間の距離1を維持する必要があります。 特定のポイントから等距離にあるポイントのセットは円です。 単位半径と点AおよびBを中心とする2つの円を作成する場合、これらの円の交点は、点Aと点Bの両方から1単位離れた点のセットを与えます。
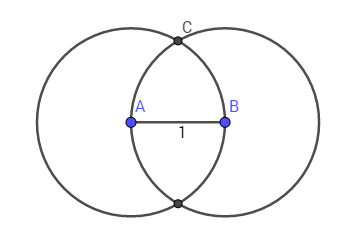
図では、円の2つの交差点の1つをCで示しています。点Cから点AおよびBまでの距離は1です。3つの点をすべて接続すると、正三角形ABCが得られます。
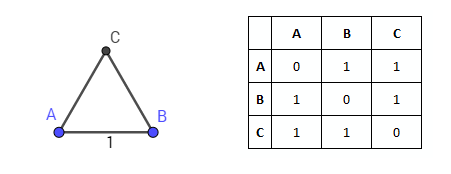
したがって、3点の離散空間は、三角形を使用して平面上に視覚化されます。 別の点Dを追加します。他の3つの点が1に等しい同じ距離に位置するように、この点を構成することは可能ですか? これを行うには、次の2つの条件を満たす必要があります。
- 3つのポイントA、B、Cは、ポイントDから描かれた円上になければなりません
- この円の半径は1に等しくなければなりません
最初の条件が満たされているのは、正三角形の周りに円を描くことができるからです:
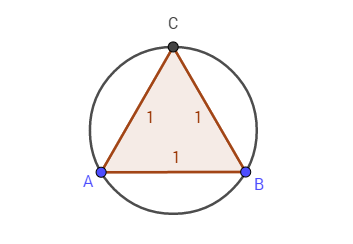
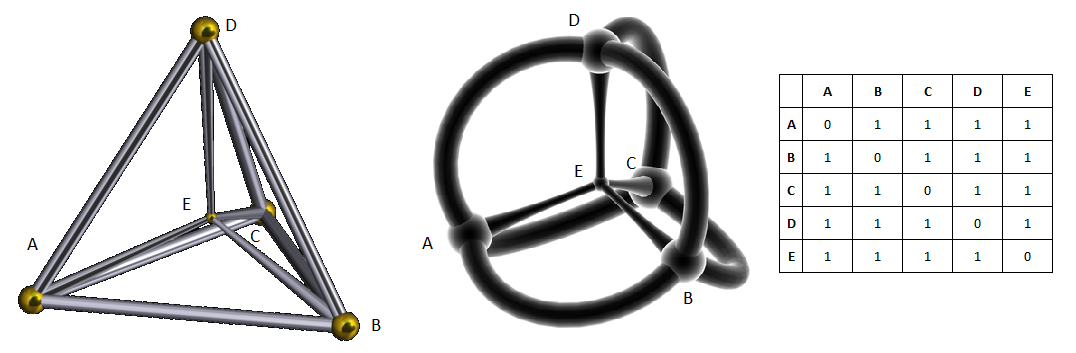
ただし、外接円の半径は次のとおりです。
 、
、
ここで、aは辺の長さです。 相互に等距離にある4つの点を平面上に描くことはできません。 2番目の条件を満たすには、点A、B、Cへの距離が1に増加するように平面から点Dを移動する必要があります。その結果、正しい四面体、つまり空間の3次元図形が得られます。
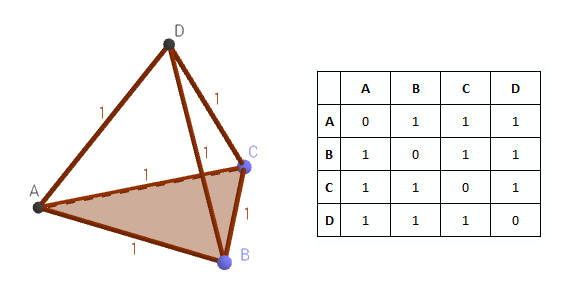
離散空間にもう1点追加すると、三角形に4番目の点を追加するのと同様の問題が再び発生します。 次に、中心に点Eを配置する4つの点A、B、C、Dが存在する単位球体を作成する必要があります。通常の四面体の周りに球体を記述することに成功しますが、その半径は単位とは異なります。
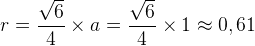
5つのポイントが互いに等距離にある図は、 5コア(五角形)と呼ばれます。 これはすでに4次元の図であり、3次元の投影は次のとおりです(左側のシュレーゲル図、右側の立体投影、Wikipedia):
点から開始して構築したすべての図の一般化は、 n-シンプレックス -n + 1頂点を持つ最も単純なn次元多面体です。
- ポイントA:1つの頂点を持つ0シンプレックス(ポイントはゼロ次元オブジェクトを持つオブジェクト)
- セグメントAB:2つの頂点を持つ1シンプレックス
- 正三角形ABC:互いに等距離にある3つの頂点を持つ2シンプレックス
- 正四面体ABCD:4つの頂点を持つ3シンプレックス
- ペンタゴンABCDE:5つの頂点を持つ4シンプレックス
- など
最初の3つのシンプレックスは、そのまま平面上に視覚化されます。 四面体を平面に投影したり、歪みのない3Dモデルにすることができます。 五角形は、コンビナトリアルプロパティを保持しながら平面に投影したり、歪みのある3Dモデルを作成したりできます。 6シンプレックスおよびより大きな次元のシンプレックスは、組み合わせ特性を保持する平面投影の形で表現できますが、より明確に達成することはできません。
したがって、視覚化が制限されている2次元または3次元の多数の点を持つ離散空間を直接視覚化することは困難です。 それにもかかわらず、少なくともある程度はその本質的な特性を維持したまま、離散空間のイメージのあるバージョンを見つけようとします。
離散空間の3D視覚化としてのThor
これまで、離散的な空間の視覚化は側面から見たものとして考えられてきました。たとえば、コンピューターの画面上など、目の前の空間のすべてのポイントを表しています。 同時に、空間を視覚化する際に最大4〜5ポイントの明瞭さを実現しました。 しかし、たとえばポイントAなど、空間内のいずれかのポイントにオブザーバーを配置するとどうなりますか? その後、他のすべてのポイントは、いくつあるかに関係なく、選択したポイントから等距離にあり、単位半径の円上に配置されます。
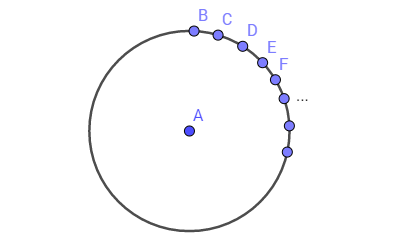
離散空間に無限に多くの点がある場合、この空間の選択された点からの視覚化は円になります。 離散空間の興味深い特徴を発見しました。 範囲外の場合、それを表すにはN-1個の測定値が必要です( Nはポイントの数です)。 しかし、離散空間内にいるとすぐに、その視覚化を2次元で構築できます。この視覚化は単位円です。
同様の円は、離散空間内の他の点に対して構築されます。 これがポイントAのままで行われ、他のポイントで別の観測者を表す場合、次の図が得られます。
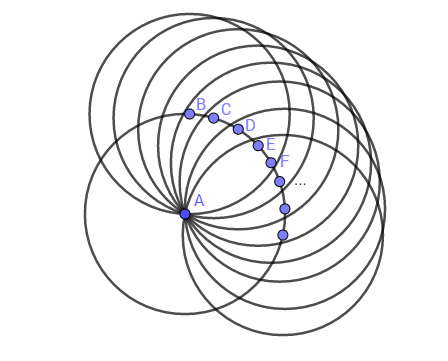
ポイントB、Cなどから構成されるすべての円は、ポイントAで交差します。つまり、これらのポイントでの観測者の離散空間の視覚化には、このポイントAが含まれます。
ただし、得られた視覚化は、多数のポイントではあまり明確ではありません。 3番目の次元を使用します。元の円を除くすべての円を次のように90度回転させます(点Aは原点にあります)。
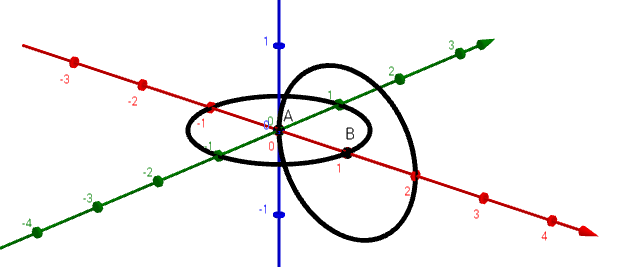
その結果、離散空間の3D視覚化として閉じた(自己触覚)トーラスが得られます。
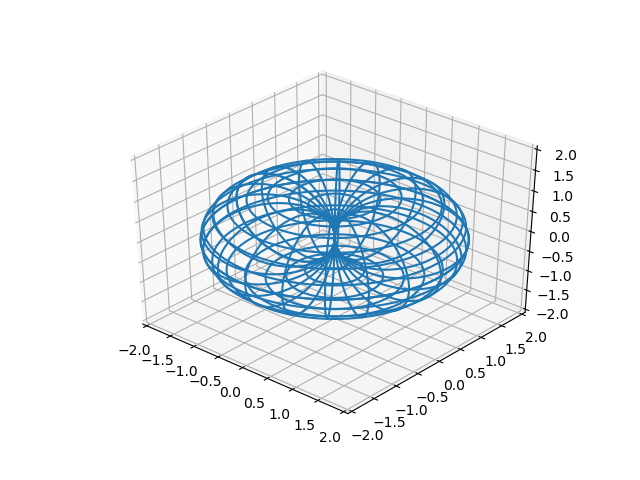
結果として得られる視覚化は、観測者がこの空間のいずれかのポイントにいて、空間の他のポイントにいる観測者を想像していることを意味します。 また、トーラスを使用した離散空間の可視化では、観測者が位置するポイントと他のポイントとの関係のみが考慮され、任意のポイント間の関係は考慮されません。
結論
- 視覚化の次元は、視覚化されたデータまたはオブジェクトの次元と常に一致するとは限りません(無次元空間および無限次元の視覚化)
- 3次元を超え、最大で無限のデータおよびその他のオブジェクトの3Dグラフィックスのフォームを見つけることができます
- 「側面から」(視覚化されたオブジェクトの外側)の視覚化の寸法は、内側(オブジェクトの任意の点から)の視覚化の寸法と異なる場合があります