こんにちは
これまで、高レベルプログラミング言語Pythonのツール群には、ACS要素の伝達関数を周波数領域から時間領域に数値変換するためのモジュールが含まれていませんでした。
逆ラプラス変換の関数は動的測定および制御システムの解析で広く使用されているため、これらの目的でPythonを使用することは非常に困難でした。精度の低い逆フーリエ変換を使用する必要があったためです[1]。
この問題は、Pythonの無料配布ライブラリ(BSDでライセンスされている)のmpmathモジュールによって解決されます。これは、浮動小数点と与えられた精度で実数および複素数算術の問題を解決するために設計されています。
2007年のモジュールの作業はFredrik Johanssonによって開始されました[2]。多くのプロジェクト参加者の助けのおかげで、mpmathは本格的な数学パッケージの機能を獲得しました。
ただし、1ステップのinvertlaplaceアルゴリズムを使用して実装された記事に記載されているトピックのみに関心があります。 例として、invertlaplaceと既知の遷移関数h(t)= e **-指定された伝達関数のtを使用して、伝達関数w(p)= 1 /(1 + p)** 2の逆ラプラス変換の結果の比較を考えます。
Invertlaplaceテスト
from mpmath import * import time mp.dps = 15# , mp.pretty = True start = time.time() def run_invertlaplace(tt,fp,ft): for i in range(0,len(tt)): print(' : %s'%ft(tt[i])) print(' : %s'%invertlaplace(fp,tt[i],method='talbot')) print(' h(t) : %s. :%s.'%(ft(tt[i]), ft(tt[i])-invertlaplace(fp,tt[i],method='talbot'))) stop = time.time() print (", : %s"%(stop-start)) tt = [0.001, 0.01, 0.1, 1, 10]# fp = lambda p: 1/(p+1)**2# ft = lambda t: t*exp(-t)# run_invertlaplace(tt,fp,ft)
テスト結果:
テスト関数値:0.000999000499833375
結果の関数値:0.000999000499833375
H(t)値:0.000999000499833375。 絶対エラー:8.57923043561212e-20。
テスト関数値:0.00990049833749168
結果の関数値:0.00990049833749168
H(t)値:0.00990049833749168 絶対エラー:3.27007646698047e-19。
テスト関数値:0.090483741803596
結果の関数値:0.090483741803596
H(t)値:0.090483741803596。 絶対エラー:-1.75215800052168e-18。
テスト関数値:0.367879441171442
結果の関数値:0.367879441171442
H(t):0.367879441171442 絶対エラー:1.2428864009344e-17。
テスト関数値:0.000453999297624849
結果の関数値:0.000453999297624849
H(t)値:0.000453999297624849 絶対エラー:4.04513489306658e-20。
逆ラプラス変換にかかった時間:0.18808794021606445
テスト例のボリュームは限られていますが、1ステップのinvertlaplaceアルゴリズムは、限られた数の時間値に対して高い精度と重要でないランタイムを持っていることも示しています。
考慮された例では、タルボット法が使用されました;他の方法の特徴は、ドキュメントで見つけることができます[3]。
ただし、逆ラプラス変換のすべての数値手法では、横座標が長時間、原点に近づく必要があることに注意してください。 横座標がラプラス領域の右端の座標の左側に移動した場合、答えは完全に間違っています。
したがって、特定の伝達関数に対する数値逆ラプラス変換の適用性を検討し、別の方法と比較して誤差を評価する必要があります。この出版物では、逆フーリエ変換法です。
1. invertlaplaceを使用した伝達関数による制御オブジェクトの遷移特性の構築
チャネルに沿って伝達関数を備えた水-水熱交換器があり、加熱水の温度が加熱水の消費量であると仮定すると、出力信号のラプラス変換は、遅延τ次のビュー:
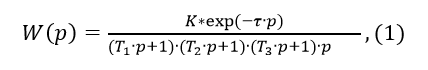
ここで、Tiはリンクの時定数です。 Kは静的なギア比です。 p¬ラプラス演算子。
伝達関数の逆ラプラス変換(1)
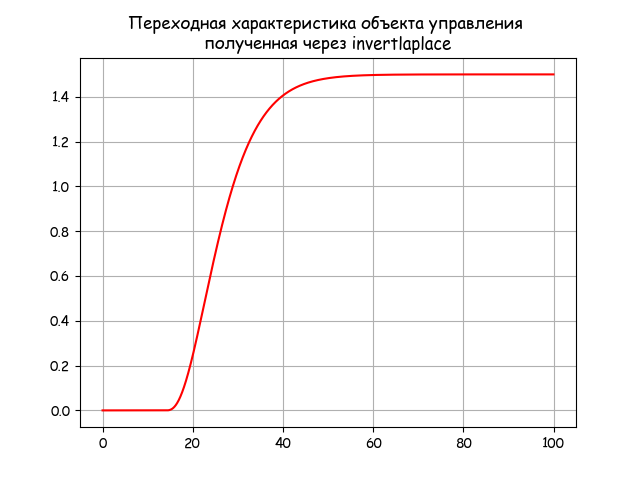
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' mp.dps = 5; mp.pretty = True def run_invertlaplace(tt,fp,tau): y=[] for i in np.arange(0,len(tt)): if tt[i]<=tau: y.append(0) else: y.append(invertlaplace(fp,tt[i],method='talbot')) return y tau=5 tt = np.arange(0,100,0.05) T1=5;T2=4;T3=4;K=1.5;tau=14 fp = lambda p: K*exp(-tau*p)/((T1*p+1)*(T2*p+1)*(T3*p+1)*p) y=run_invertlaplace(tt,fp,tau) plt.title(' \n, invertlaplace ') plt.plot(tt,y,'r') plt.grid(True) plt.show()
遅延とセルフアライメントを備えたオブジェクトの遷移特性を取得します。
2. invertlaplaceを使用した伝達関数によるPIDコントローラーの過渡応答の構築
PIDコントローラーの伝達関数のラプラスイメージは次のとおりです。
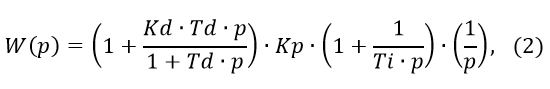
ここで、Td、Ti-時定数、リンクの差別化および統合。 Kp、Kd-比例および微分リンクの静的透過係数。
pはラプラス演算子です。
伝達関数の逆ラプラス変換(2)
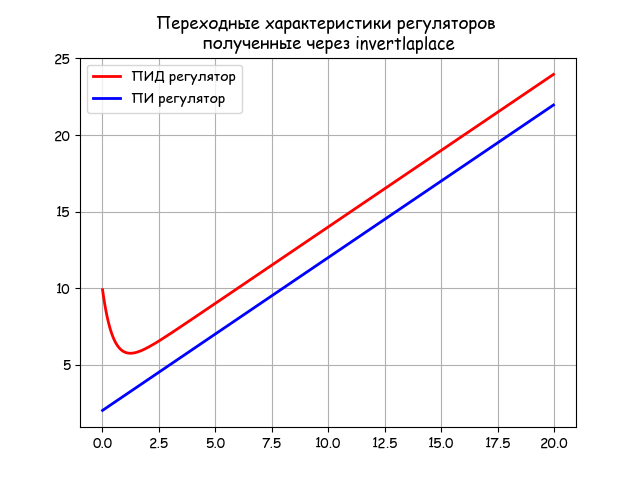
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' mp.dps = 5; mp.pretty = True tt = np.arange(0.01,20,0.05) Kp=2;Ti=2;Kd=4;Td=0.5 fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p) y=[invertlaplace(fp,tt[i],method='talbot') for i in np.arange(0,len(tt))] Kd=0 fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p) y1=[invertlaplace(fp,tt[i],method='talbot') for i in np.arange(0,len(tt))] plt.title(' \n, invertlaplace ') plt.plot(tt,y,'r', color='r',linewidth=2, label='-') plt.plot(tt,y1, color='b', linewidth=2, label='-') plt.grid(True) plt.legend(loc='best') plt.show()
リストによれば、Kd = 0を使用して、PIDコントローラーの過渡応答だけでなく、PIコントローラーも取得できます。
3.典型的なACSオブジェクトに適用される数値逆ラプラス逆位法の精度の評価
記事の冒頭に示したinvertlaplaceの適用可能性に関する警告を考慮に入れて、さらなるプレゼンテーションでは、遅延と自己整合を伴うオブジェクト、および規制当局へのメソッドの適用可能性が証明されました。
数値解の精度の問題は不明のままです。 明確にするために、伝達関数(2)と[1]で与えられた遷移関数への次の正確な変換を使用します。
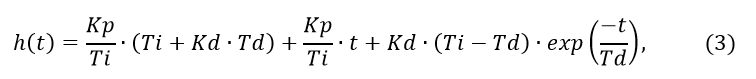
テスト関数を使用した逆変換精度(2)(3)
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' mp.dps = 15; mp.pretty = True tt = np.arange(0.01,20,0.01) Kp=2;Ti=2;Kd=4;Td=0.5 fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p) ft = lambda t:(Kp/Ti)*(Ti+Kd*Td)+(Kp/Ti)*t+Kd*(Ti-Td)*exp(-t/Td) y=np.array([invertlaplace(fp,tt[i],method='talbot') for i in np.arange(0,len(tt))]) y1=np.array([ft(tt[i]) for i in np.arange(0,len(tt))]) z=y-y1 plt.title(' invertlaplace ') plt.plot(tt,z,'r', color='r',linewidth=1, label=' ') plt.grid(True) plt.legend(loc='best') plt.show()
次のグラフが表示されます。
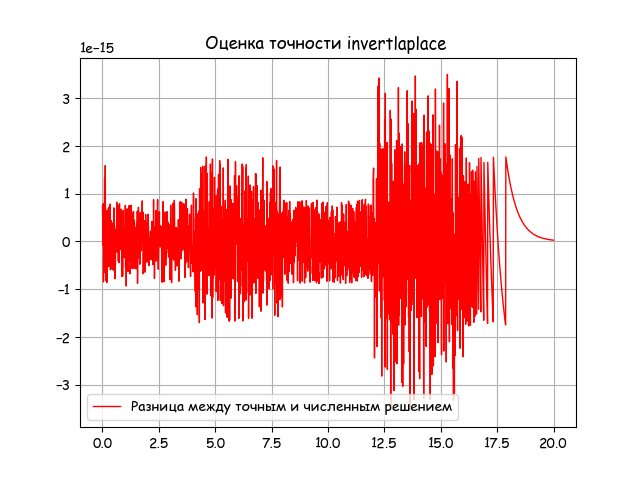
グラフは、伝達関数の縮小クラスの数値法の誤差が無視できることを示しています(3 * 10 ^ -15)。 さらに、数値メソッドのエラーは、値mp.dpsおよびステップtt [i + 1] -tt [i]を設定することで制御できます(リストを参照)。
4.典型的なACSオブジェクトに適用される逆ラプラス変換invertlaplaceの数値的手法と逆フーリエ変換の数値的手法の精度の比較評価
遷移特性の構築は、逆フーリエ変換式[1]に基づいて行うことができます。
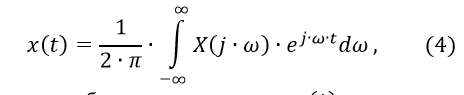
ここで、X(j∙ω)は元のx(t)のフーリエ画像です。
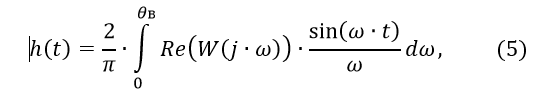
ここで、Re(W(j∙ω))は規制対象の実際の周波数特性です。
計算の積分の上限θとして、モジュラスRe(W(j∙ω))が小さな値(0.05 * Kなど)に減少し、ωがさらに増加してもこの値を超えない周波数ωの値を取ります。
最初に、関係(5)で積分の上限を定義します。 これを行うには、伝達関数(1)を使用します。まずユニットの影響を取り除き、右側に演算子pを掛けます。
関数Reのプロット(W(j∙ω))
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' ww= np.arange(0,0.6,0.005) T1=25;T2=21;T3=12;K=0.37;tau=14 def invertfure(w): j=(-1)**0.5 return ((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real) z=[invertfure(w) for w in ww] plt.title(' \n Re(W(j*w)) ') plt.plot(ww,z,'r') plt.grid(True) plt.show()
チャート:
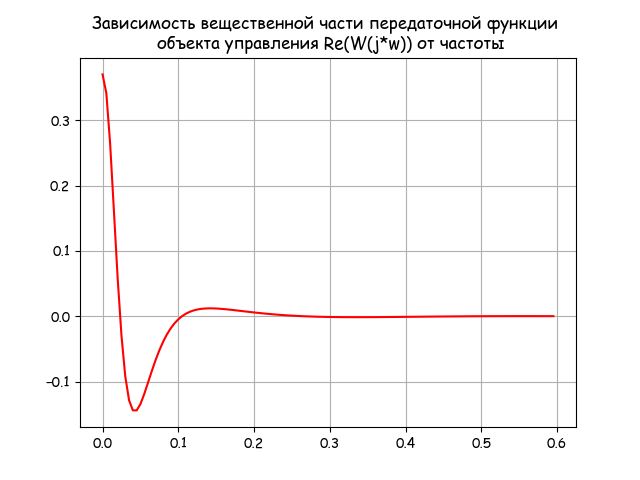
グラフからわかるように、関係(5)の上限積分値は0.6に等しくすることができます。これは、周波数がさらに増加すると、制御オブジェクトの伝達関数の実部がゼロ値を保持するためです。
(5)を使用して、逆フーリエ変換法により制御オブジェクトの遷移特性を取得します。
フーリエ過渡応答
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' from scipy.integrate import quad tt=np.arange(0,200,1) T1=25;T2=21;T3=12;K=0.37;tau=14 def invertfure(w,t): j=(-1)**0.5 return (2/np.pi)*((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real*(np.sin(w*t)/w)) z=[quad(lambda w: invertfure(w,t),0, 0.6)[0] for t in tt] plt.title(' , \n ') plt.plot(tt,z,'r') plt.grid(True) plt.show()
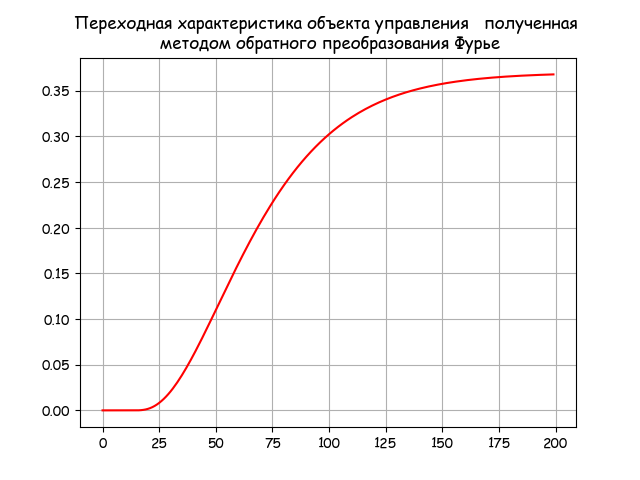
逆ラプラス変換とフーリエ変換の精度の比較評価のために、[1]で与えられる制御オブジェクトの伝達関数(1)の正確な変換を使用します。
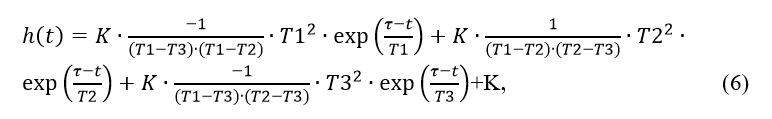
正確な変換(6)から、逆ラプラス変換(1)と逆フーリエ変換を順番に減算します。 両方の方法の精度の比較を特徴付けるグラフを作成するために、プログラムの次のリストをコンパイルします。
逆ラプラス法とフーリエ変換法の比較分析
# -*- coding: utf8 -*- import numpy as np from scipy.integrate import quad import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' tt = np.arange(0,100,0.01) T1=25;T2=21;T3=12;K=0.37;tau=14 def invertfure(w,t): j=(-1)**0.5 return (2/np.pi)*((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real*(np.sin(w*t)/w)) z=np.array([quad(lambda w: invertfure(w,t),0, 0.6)[0] for t in tt]) def h(t): if t<=tau: g=0 else: g=(-K*(T1**2)*np.exp((tau-t)/T1)/((T1-T3)*(T1-T2)))+(K*(T2**2)*np.exp((tau-t)/T2)/((T1-T2)*(T2-T3)))+(-K*(T3**2)*np.exp((tau-t)/T3)/((T1-T3)*(T2-T3)))+K return g q=np.array([h(t) for t in tt]) from mpmath import * mp.dps = 5; mp.pretty = True def run_invertlaplace(tt,fp,tau): y=[] for i in np.arange(0,len(tt)): if tt[i]<=tau: y.append(0) else: y.append(invertlaplace(fp,tt[i],method='talbot')) return y fp = lambda p: K*exp(-tau*p)/((T1*p+1)*(T2*p+1)*(T3*p+1)*p) y=np.array(run_invertlaplace(tt,fp,tau)) plt.title(' \n ') plt.plot(tt,qy,'b',linewidth=2, label= ' ') plt.plot(tt,qz,'r',linewidth=2, label=' ') plt.legend(loc='best') plt.grid(True) plt.show()
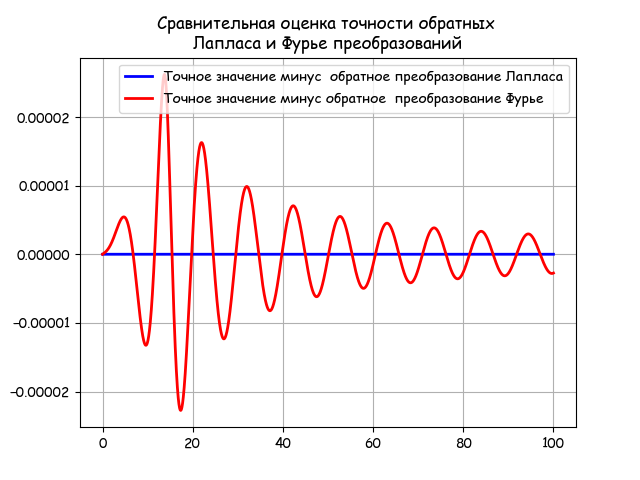
グラフから、数値逆ラプラス変換はフーリエ変換よりも安定であり、さらに、正確な解と一致することがわかります。
結論
1.逆ラプラス変換とフーリエ変換の数値的方法の比較分析が実行され、逆ラプラス変換の優れた精度と安定性が示されます。
2.オブジェクトの基本伝達関数と自走砲の要素の逆ラプラス変換にmpmath Pythonライブラリを使用する可能性が示されています。