
長い間、機械学習のトピックに興味がありました。 プログラミングなしでマシンがどのように学習および予測できるのか、驚きました。 私はいつもこれに魅了されましたが、このトピックを詳細に研究したことはありませんでした。 時間は貴重なリソースであり、機械学習について読み込もうとするたびに、情報に圧倒されました。 これらすべてをマスターすることは難しく、時間がかかるように見えました。 また、私は機械学習を掘り下げ始めても必要な数学的知識を持っていないと確信しました。
しかし、最終的に、私はこれに異なるアプローチをすることにしました。 少しずつ、基本的なことから始めて徐々に複雑なものに移り、できるだけ多くの基本的なことをカバーしようとして、コードのさまざまな概念を再現しようとします。 言語としてGoを選択しました。これは私のお気に入りの言語の1つです。さらに、RやPythonのような従来の機械学習言語にも精通していません。
はじめに
主な学習プロセスがどの段階であるかを理解するための簡単なモデルを作成することから始めましょう。
ワシントン州キング郡の住宅価格を予測するとします。
最初に、実際の統計を含むデータセットを見つける必要があります。 それに基づいて、モデルを作成します。
次の構造を持つcsvファイルの形式で提供されます。
kc_house_data.csv
id,date,price,bedrooms,bathrooms,sqft_living,sqft_lot,floors,waterfront,view,condition,grade,sqft_above,sqft_basement,yr_built,yr_renovated,zipcode,lat,long,sqft_living15,sqft_lot15 "7129300520","20141013T000000",221900,3,1,1180,5650,"1",0,0,3,7,1180,0,1955,0,"98178",47.5112,-122.257,1340,5650 "6414100192","20141209T000000",538000,3,2.25,2570,7242,"2",0,0,3,7,2170,400,1951,1991,"98125",47.721,-122.319,1690,7639 "5631500400","20150225T000000",180000,2,1,770,10000,"1",0,0,3,6,770,0,1933,0,"98028",47.7379,-122.233,2720,8062
ファイル内には必要なものがすべてあります。 各行には多くの情報が含まれており、住宅価格の予測に正確に役立つものを把握する必要があります。
必要なもの:
- モデルを選択してください。
- データを理解する。
- 仕事のためにデータを準備します。
- モデルをトレーニングします。
- モデルをテストします。
- モデルを視覚化します。
1.モデルの選択
最も一般的なモデルの1つである線形回帰を使用します。
このモデルは他の多くのモデルの根底にあり、新しいデータ分析を開始するのに適しています。 結果のモデルが十分に予測できる場合は、より複雑なモデルに進む必要はありません。
線形回帰を詳しく見てみましょう。

このグラフは、2つの変数間の関係を示しています。
縦軸(Y)は、従属変数(この場合は住宅価格)を反映しています。 水平軸(X)は、いわゆる独立変数を反映しています。この場合、 寝室、浴室、sqft_livingなど、データセットの他のデータを使用できます。
グラフ上の円は、特定のx値の y 値です (y は xに 依存します)。 赤い線は線形回帰です。 この行はすべての値を通過し、特定のxの可能なy値を予測するために使用できます。
私たちの目標は、モデルを訓練して、タスクの赤い線を構築することです。
線形関数の形式はy = ax + b
ことを思い出してください。 彼女を見つける必要があります。 より正確には、データに最適なb
とb
値を見つける必要があります。
2.データを理解する
どのモデルが必要で、どのアプローチを使用するかがわかっています。 データを分析し、それらが私たちのタスクに適しているかどうかを理解することは残っています。
線形回帰モデルのデータは正規分布する必要があります 。 つまり、データヒストグラムはベルの形である必要があります。
データに基づいてグラフを作成し、必要に応じて分布しているかどうかを確認しましょう。 これを行うには、最後にコードを書きます!
便利なパッケージ:
- 標準ライブラリのencoding / csvは、データセットをダウンロードしてその内容を解析するのに役立ちます。
- github.com/gonum/plotは、チャートの作成に役立ちます。
このコードはCSVを開き、IDと日付を除くすべての列のヒストグラムを描画します。 したがって、モデルトレーニングに使用する列を選択できます。
// we open the csv file from the disk f, err := os.Open("./datasets/kc_house_data.csv") if err != nil { log.Fatal(err) } defer f.Close() // we create a new csv reader specifying // the number of columns it has salesData := csv.NewReader(f) salesData.FieldsPerRecord = 21 // we read all the records records, err := salesData.ReadAll() if err != nil { log.Fatal(err) } // by slicing the records we skip the header records = records[1:] // we iterate over all the records // and keep track of all the gathered values // for each column columnsValues := map[int]plotter.Values{} for i, record := range records { // we want one histogram per column, // so we will iterate over all the columns we have // and gather the date for each in a separate value set // in columnsValues // we are skipping the ID column and the Date, // so we start on index 2 for c := 2; c < salesData.FieldsPerRecord; c++ { if _, found := columnsValues[c]; !found { columnsValues[c] = make(plotter.Values, len(records)) } // we parse each close value and add it to our set floatVal, err := strconv.ParseFloat(record[c], 64) if err != nil { log.Fatal(err) } columnsValues[c][i] = floatVal } } // once we have all the data, we draw each graph for c, values := range columnsValues { // create a new plot p, err := plot.New() if err != nil { log.Fatal(err) } p.Title.Text = fmt.Sprintf("Histogram of %s", records[0][c]) // create a new normalized histogram // and add it to the plot h, err := plotter.NewHist(values, 16) if err != nil { log.Fatal(err) } h.Normalize(1) p.Add(h) // save the plot to a PNG file. if err := p.Save( 10*vg.Centimeter, 10*vg.Centimeter, fmt.Sprintf("./graphs/%s_hist.png", records[0][c]), ); err != nil { log.Fatal(err) } }
このコードは一連のグラフを生成します。 これらのうち、正規分布の条件を最もよく満たすものを選択する必要があります(ベル型の曲線)。
ここに私が選んだチャートがあります( すべてのヒストグラム ):

これは、グレード列のグラフです。 正規分布の観点からは理想的ではありませんが、これで十分です。 すべてのヒストグラムを見ると、使用できるものがさらにいくつか見つかります。 結果のモデルの予測が不十分な場合は、データセットの別の列を基準として選択します。
その場合:Gradは、建物の品質レベルの評価です。 建物のBUILDING GRADE
のセクションで、建物の品質レベルの詳細をご覧ください。
3.データを準備します
そのため、モデルトレーニングには、ダウンロードしたデータセットを使用します。 しかし、モデルが十分に正確であるかどうかをどのようにして知るのでしょうか?
テストしてみましょう。これには同じデータセットを使用します。 1つのデータセットがトレーニングとテストに役立つように、2つの部分に分けます。1つはトレーニング用、もう1つはテスト用です。 これは通常のアプローチです。
データの80%についてトレーニングし、残りの20%をテストに使用します。 他にも十分に確立された関係がありますが、適切なオプションを選択するには、ほとんどの場合、試行錯誤して行動する必要があります。
モデルを再トレーニングしないように、適切なトレーニングとテストのためにデータの十分性のバランスを取る必要があります。
// we open the csv file from the disk f, err := os.Open("./datasets/kc_house_data.csv") if err != nil { log.Fatal(err) } defer f.Close() // we create a new csv reader specifying // the number of columns it has salesData := csv.NewReader(f) salesData.FieldsPerRecord = 21 // we read all the records records, err := salesData.ReadAll() if err != nil { log.Fatal(err) } // save the header header := records[0] // we have to shuffle the dataset before splitting // to avoid having ordered data // if the data is ordered, the data in the train set // and the one in the test set, can have different // behavior shuffled := make([][]string, len(records)-1) perm := rand.Perm(len(records) - 1) for i, v := range perm { shuffled[v] = records[i+1] } // split the training set trainingIdx := (len(shuffled)) * 4 / 5 trainingSet := shuffled[1 : trainingIdx+1] // split the testing set testingSet := shuffled[trainingIdx+1:] // we write the splitted sets in separate files sets := map[string][][]string{ "./datasets/training.csv": trainingSet, "./datasets/testing.csv": testingSet, } for fn, dataset := range sets { f, err := os.Create(fn) if err != nil { log.Fatal(err) } defer f.Close() out := csv.NewWriter(f) if err := out.Write(header); err != nil { log.Fatal(err) } if err := out.WriteAll(dataset); err != nil { log.Fatal(err) } out.Flush() }
上記のコードは2つのファイルを生成します。
- training.csv-モデルをトレーニングするためのレコードが含まれています。
- testing.csv-テスト用のレコードが含まれています。
4.モデルのトレーニング
それでは、学習を始めましょう。 これにはさまざまなパッケージが適しています。github.com/ sajari / regressionを使用し 、すべてが実装されます。
もちろん、すべてをゼロから書くこともできますが、今のところは複雑にしません。
最初に、 training.csv
からレコードをダウンロードし、それらを調べて、 Price
列とGrade
列のデータをモデルに入れます。
次に、線形関数を見つけるためにモデルをトレーニングしましょう。
// we open the csv file from the disk f, err := os.Open("./datasets/training.csv") if err != nil { log.Fatal(err) } defer f.Close() // we create a new csv reader specifying // the number of columns it has salesData := csv.NewReader(f) salesData.FieldsPerRecord = 21 // we read all the records records, err := salesData.ReadAll() if err != nil { log.Fatal(err) } // In this case we are going to try and model our house price (y) // by the grade feature. var r regression.Regression r.SetObserved("Price") r.SetVar(0, "Grade") // Loop of records in the CSV, adding the training data to the regression value. for i, record := range records { // Skip the header. if i == 0 { continue } // Parse the house price, "y". price, err := strconv.ParseFloat(records[i][2], 64) if err != nil { log.Fatal(err) } // Parse the grade value. grade, err := strconv.ParseFloat(record[11], 64) if err != nil { log.Fatal(err) } // Add these points to the regression value. r.Train(regression.DataPoint(price, []float64{grade})) } // Train/fit the regression model. r.Run() // Output the trained model parameters. fmt.Printf("\nRegression Formula:\n%v\n\n", r.Formula)
実行の完了後、式を取得します。
Regression Formula: Predicted = -1065201.67 + Grade*209786.29
5.モデルのテスト
生成された数式では、グレード列に基づいて販売価格を予測できると想定されています。
数式をテストします。 これを行うには、前に作成したtesting.csv
ファイルを使用します。
テストデータはありますが、出力にはまだデータが必要です。これにより、式の正確さを理解できます。 これを行うには、決定係数の値を使用します。
決定係数は、独立変数を予測できる従属変数の量を示します。 この場合、グレード列のデータに基づいて予測できる住宅価格の数。
生成された係数値は、0〜1の範囲にあります(値が大きいほど良い)。
決定係数を生成するコードは次のとおりです。
func main() { // we open the csv file from the disk f, err := os.Open("./datasets/testing.csv") if err != nil { log.Fatal(err) } defer f.Close() // we create a new csv reader specifying // the number of columns it has salesData := csv.NewReader(f) salesData.FieldsPerRecord = 21 // we read all the records records, err := salesData.ReadAll() if err != nil { log.Fatal(err) } // by slicing the records we skip the header records = records[1:] // Loop over the test data predicting y observed := make([]float64, len(records)) predicted := make([]float64, len(records)) var sumObserved float64 for i, record := range records { // Parse the house price, "y". price, err := strconv.ParseFloat(records[i][2], 64) if err != nil { log.Fatal(err) } observed[i] = price sumObserved += price // Parse the grade value. grade, err := strconv.ParseFloat(record[11], 64) if err != nil { log.Fatal(err) } // Predict y with our trained model. predicted[i] = predict(grade) } mean := sumObserved / float64(len(observed)) var observedCoefficient, predictedCoefficient float64 for i := 0; i < len(observed); i++ { observedCoefficient += math.Pow((observed[i] - mean), 2) predictedCoefficient += math.Pow((predicted[i] - mean), 2) } rsquared := predictedCoefficient / observedCoefficient // Output the R-squared to standard out. fmt.Printf("R-squared = %0.2f\n\n", rsquared) } func predict(grade float64) float64 { return -1065201.67 + grade*209786.29 }
predict
関数は、テストデータセットを使用して生成した線形方程式であることに注意してください。
取得したものは次のとおりです。
R-squared = 0.46
不完全です。
回帰を視覚化し、改善を試みましょう。
6.モデルを視覚化する
視覚化のために、さらにコードを記述します 。
// we open the csv file from the disk f, err := os.Open("kc_house_data.csv") if err != nil { log.Fatal(err) } defer f.Close() df := dataframe.ReadCSV(f) // pts will hold the values for plotting. pts := make(plotter.XYs, df.Nrow()) // ptsPred will hold the predicted values for plotting. ptsPred := make(plotter.XYs, df.Nrow()) yVals := df.Col("price").Float() for i, floatVal := range df.Col("grade").Float() { pts[i].X = floatVal pts[i].Y = yVals[i] ptsPred[i].X = floatVal ptsPred[i].Y = predict(floatVal) } // Create the plot. p, err := plot.New() if err != nil { log.Fatal(err) } pXLabel.Text = "grade" pYLabel.Text = "house price" p.Add(plotter.NewGrid()) // Add the scatter plot points for the observations. s, err := plotter.NewScatter(pts) if err != nil { log.Fatal(err) } s.GlyphStyle.Radius = vg.Points(2) s.GlyphStyle.Color = color.RGBA{R: 0, G: 0, B: 255, A: 255} // Add the line plot points for the predictions. l, err := plotter.NewLine(ptsPred) if err != nil { log.Fatal(err) } l.LineStyle.Width = vg.Points(0.5) l.LineStyle.Dashes = []vg.Length{vg.Points(2), vg.Points(2)} l.LineStyle.Color = color.RGBA{R: 255, G: 0, B: 0, A: 255} // Save the plot to a PNG file. p.Add(s, l) if err := p.Save(10*vg.Centimeter, 10*vg.Centimeter, "./graphs/first_regression.png"); err != nil { log.Fatal(err) }
そして最後に、最初の線形回帰を取得しました。

よく見ると、青い円は直線ではなく曲線に配置するのが最適であることが明らかになります。
結果を改善するために、現在の線形式を放物線式y = ax + bx^2 + c
置き換えることができます。
また、Grade列を使用してx変数を表します 。新しい数式は次のようになります。
price = a * grade + b * grade^2 + c
トレーニング機能のコードを更新します 。
// ... everything is the same up to here r.SetVar(1, "Grade2") // now we add one more variable, Grade^2 // ... everything is the same also here // except we are now addin the new variable r.Train(regression.DataPoint(price, []float64{grade, math.Pow(grade, 2)})) // ...
新しい数式を取得します。
Regression Formula: Predicted = 1639674.31 + Grade*-473161.41 + Grade2*42070.46
これで再び決定係数を計算できます:
R-squared = 0.52
より良い! できるだけ1に近い値を取得する必要があることに注意してください。
// ... we open the file etc // pts will hold the values for plotting. pts := make(plotter.XYs, df.Nrow()) yVals := df.Col("price").Float() for i, floatVal := range df.Col("grade").Float() { pts[i].X = floatVal pts[i].Y = yVals[i] } // Create the plot. p, err := plot.New() if err != nil { log.Fatal(err) } pXLabel.Text = "grade" pYLabel.Text = "house price" p.Add(plotter.NewGrid()) // Add the scatter plot points for the observations. s, err := plotter.NewScatter(pts) if err != nil { log.Fatal(err) } s.GlyphStyle.Radius = vg.Points(2) s.GlyphStyle.Color = color.RGBA{R: 0, G: 0, B: 255, A: 255} curve := plotter.NewFunction(predict) curve.LineStyle.Width = vg.Points(3) curve.LineStyle.Dashes = []vg.Length{vg.Points(3), vg.Points(3)} curve.LineStyle.Color = color.RGBA{R: 255, G: 0, B: 0, A: 255} // Save the plot to a PNG file. p.Add(s, curve) if err := p.Save(10*vg.Centimeter, 10*vg.Centimeter, "./graphs/second_regression.png"); err != nil { log.Fatal(err) }
更新されたスケジュール:
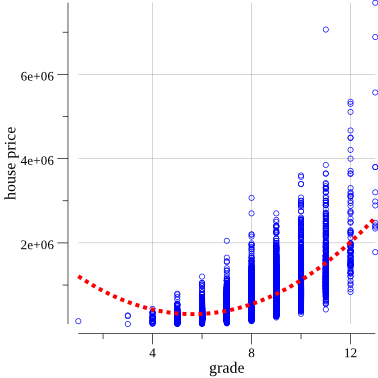
良くなった。
必要に応じて、決定係数を1に近づけるためにいくつかの改善を行うことができます-実験。 異なる変数を変更または組み合わせて、モデルの改善を試みることもできます。
予測式に満足していると仮定して、それを使い始めましょう。 キング郡のグレード3の家を売却することで稼ぐことができる金額を調べたいとします。 式にグレード値を挿入し、価格を取得します。
598824.2200000001 USD
線形回帰モデルとGoパッケージの使用に関するこの入門書がお役に立てば幸いです。機械学習を学び始めることができます。