バイナリグラフ検索

バイナリ検索は、私が知っている最も基本的なアルゴリズムの1つです。 比較可能なアイテムとターゲットアイテムのソートされたリストがある場合、バイナリ検索はリストの中央を検索し、値をターゲットアイテムと比較します。 目標が大きい場合、リストの半分未満で繰り返します。逆も同様です。



各比較で、バイナリ検索アルゴリズムは検索スペースを半分に分割します。 これのおかげで、これ以上はありません $$$\ log（n）$ ランタイム比較 $$$O（\ log n）$ 。 美しい、効果的、便利。



ただし、常に別の角度から見ることができます。



グラフでバイナリ検索を実行しようとするとどうなりますか？ 幅優先検索や深さ検索など、ほとんどのグラフ検索アルゴリズムは線形時間を必要とし、かなり賢い人によって発明されました。 したがって、グラフ内のバイナリ検索が意味をなす場合、従来の検索アルゴリズムがアクセスできる情報よりも多くの情報を使用する必要があります。



リスト内のバイナリ検索の場合、この情報はリストがソートされているという事実であり、検索を制御するために、数値を検索対象の要素と比較できます。 しかし、実際には、最も重要な情報は要素の比較可能性に関係していません。 それは、各段階で探索空間の半分を取り除くことができるという事実にあります。 「目標値との比較」の段階は、「これは私が探していた値ですか？」などのクエリに応答するブラックボックスとして認識できます。答えは「はい」または「いいえ、ここでは良く見えます」









クエリに対する回答が非常に有用な場合、つまり、各段階で大量の検索スペースを分離できる場合、適切なアルゴリズムが得られたようです。 実際、Emanjome-Zade、Kempe、Singalによる 2015年の記事で定義されている自然なグラフモデルは次のとおりです。



入力として無向の重み付きグラフを取得します $$$G =（V、E）$ 重み付き $$$w_e$ で $$$e \ in E$ 。 グラフ全体が表示され、「Is the top」の形式で質問できます $$$v$ ”答えは2つの選択肢があります。

• はい（勝ちました！）
• いいえ $$$e =（v、w）$ の端です $$$v$ からの最短経路上 $$$v$ 目的のピークに。

私たちの目標は、クエリの最小数に対して適切なピークを見つけることです。



明らかに、これは次の場合にのみ機能します $$$G$ は接続されたグラフですが、記事に記載されているもののわずかなバリエーションは、無関係のグラフに対して機能します。 （一般に、これは有向グラフには当てはまりません。）



グラフが線の場合、タスクはバイナリ検索と同じ基本概念が使用されるという意味で、バイナリ検索に「縮小」されます。グラフの中央から開始し、クエリに応答して得られるエッジは、グラフの半分で検索を続行します。









そして、この例をもう少し複雑にすると、一般化が明らかになります。









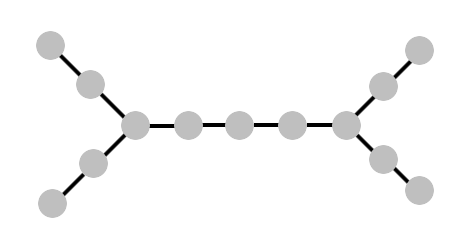
ここで、再び「中央のピーク」から始めます。要求に対する答えは、2つの半分のいずれかから私たちを救います。 しかし、次はどのようにして次の頂点を選択できるのでしょうか？ それは明らかなはずです-私たちが自分自身を見つける任意の半分の「中央ピーク」を選択してください。 この選択は、明白な対称性がなくても機能するルールに形式化することができ、結局のところ、この選択は常に正しいでしょう。



定義：加重グラフの中央値 $$$G$ 頂点のサブセットに関連 $$$S \サブセットV$ トップです $$$v \ in V$ （オプションであります $$$S$ ）、頂点間の距離の合計を最小化します $$$S$ >。 より正式には、最小化

$$

$$\ Phi_S（v）= \ sum_ {u \ in S} d（v、u）$$

どこで $$$d（u、v）$ -からの最短経路に沿ったエッジの重みの合計 $$$v$ 前に $$$u$ 。



グラフ上のクエリを使用してこのようなモデルにバイナリ検索を一般化すると、次のアルゴリズムにつながり、各ステップで中央値を求めることで検索スペースが制限されます。



アルゴリズム：グラフ内のバイナリ検索。 グラフは入力として使用されます $$$G =（V、E）$ 。

• 多くの候補者から始めます $$$S = V$ 。
• 適切なピークが見つかるまで $$$| S | > 1$ ：
  
  
  • メディを頼む $$$v$ 多くの $$$S$ 正しい頂点が見つかったら停止します。
  • そうでなければ $$$e =（v、w）$ リクエストに応じて受信したエッジになります。 すべての頂点のセットを計算する $$ そのために $$$e$ からの最短経路です $$$v$ で $$$x$ 。 このセットを呼び出す $$$T$ 。
  • 交換 $$$S$ に $$$S \キャップT$ 。
• 残りの唯一の頂点を印刷する $$$S$

実際、すぐにわかるように、Pythonの実装はほとんど同じくらい簡単です。 ジョブの最も重要な部分は、中央値とセットを計算することです $$$T$ 。 これらの操作は両方とも、最短経路を計算するためのダイクストラのアルゴリズムの小さな種類です 。



Emamjome-Zadehと彼の同僚（5ページのページの約半分） によって単純で適切に定式化された定理は、アルゴリズムが必要とするのは $$$O（\ log（n））$ バイナリ検索と同じ数のクエリがあります。



実装を掘り下げる前に、1つのトリックを検討する価値があります。 もはやないことが保証されているにもかかわらず $$$\ log（n）$ クエリ、ダイクストラのアルゴリズムの実装のため、対数アルゴリズムは絶対に取得しません。 そのような状況で私たちにとって何が役立つでしょうか？



ここでは、「理論」を使用します-後でアプリケーションを見つけるための架空のタスクを作成します（コンピューターサイエンスで非常にうまく使用されます）。 この場合、クエリメカニズムをブラックボックスとして扱います。 要求は時間がかかり、最適化が必要なリソースであると想像するのは自然です。 たとえば、著者が追加の記事で書いたように、グラフはデータセットのグループのセットである場合があり、リクエストにはデータを見て、どのクラスターを分割するか、または2つのクラスターを結合するかを伝える人の介入が必要です。 もちろん、グループ化時にグラフが大きすぎて処理できないため、中央値検索アルゴリズムを暗黙的に定義する必要があります。 しかし、最も重要なことは明らかです。クエリがアルゴリズムの中で最も高価な部分である場合があります。



さて、これをすべて実現しましょう！ 常にGithubにある完全なコード。

アルゴリズムを実装します

ダイクストラのアルゴリズムの小さなバリエーションから始めます。 ここでは、入力として「開始」ポイントが与えられ、出力として、可能なすべての終了頂点へのすべての最短パスのリストが作成されます。



裸のグラフデータ構造から始めます。

from collections import defaultdict from collections import namedtuple Edge = namedtuple('Edge', ('source', 'target', 'weight')) class Graph: #      def __init__(self, vertices, edges=tuple()): self.vertices = vertices self.incident_edges = defaultdict(list) for edge in edges: self.add_edge( edge[0], edge[1], 1 if len(edge) == 2 else edge[2] #   ) def add_edge(self, u, v, weight=1): self.incident_edges[u].append(Edge(u, v, weight)) self.incident_edges[v].append(Edge(v, u, weight)) def edge(self, u, v): return [e for e in self.incident_edges[u] if e.target == v][0]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、ダイクストラのアルゴリズムのほとんどの作業はグラフ検索中に蓄積された情報を追跡することなので、「出力」データ構造を決定します。検出された最短パスへのバックポインターとエッジウェイトを持つ辞書です。

 class DijkstraOutput: def __init__(self, graph, start): self.start = start self.graph = graph #        v self.distance_from_start = {v: math.inf for v in graph.vertices} self.distance_from_start[start] = 0 #        #        self.predecessor_edges = {v: [] for v in graph.vertices} def found_shorter_path(self, vertex, edge, new_distance): #        self.distance_from_start[vertex] = new_distance if new_distance < self.distance_from_start[vertex]: self.predecessor_edges[vertex] = [edge] else: # ""     self.predecessor_edges[vertex].append(edge) def path_to_destination_contains_edge(self, destination, edge): predecessors = self.predecessor_edges[destination] if edge in predecessors: return True return any(self.path_to_destination_contains_edge(e.source, edge) for e in predecessors) def sum_of_distances(self, subset=None): subset = subset or self.graph.vertices return sum(self.distance_from_start[x] for x in subset)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、実際のダイクストラアルゴリズムは、幅優先検索（優先度キューによって駆動）を実行します。 $$$G$ 短いパスを見つけたときにメタデータを更新します。

 def single_source_shortest_paths(graph, start): '''             .   DijkstraOutput. ''' output = DijkstraOutput(graph, start) visit_queue = [(0, start)] while len(visit_queue) > 0: priority, current = heapq.heappop(visit_queue) for incident_edge in graph.incident_edges[current]: v = incident_edge.target weight = incident_edge.weight distance_from_current = output.distance_from_start[current] + weight if distance_from_current <= output.distance_from_start[v]: output.found_shorter_path(v, incident_edge, distance_from_current) heapq.heappush(visit_queue, (distance_from_current, v)) return output
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最後に、中央値を見つけて計算するルーチンを実装します $$$T$ ：

 def possible_targets(graph, start, edge): '''     G = (V,E),   v  V   e,  v,    w, ,  e      v  w. ''' dijkstra_output = dijkstra.single_source_shortest_paths(graph, start) return set(v for v in graph.vertices if dijkstra_output.path_to_destination_contains_edge(v, edge)) def find_median(graph, vertices): '''    output    ,         ''' best_dijkstra_run = min( (single_source_shortest_paths(graph, v) for v in graph.vertices), key=lambda run: run.sum_of_distances(vertices) ) return best_dijkstra_run.start
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして今、アルゴリズムの中核

 QueryResult = namedtuple('QueryResult', ('found_target', 'feedback_edge')) def binary_search(graph, query): '''          "  x  ?"    -  "   !",  "       ". ''' candidate_nodes = set(x for x in graph.vertices) #  while len(candidate_nodes) > 1: median = find_median(graph, candidate_nodes) query_result = query(median) if query_result.found_target: return median else: edge = query_result.feedback_edge legal_targets = possible_targets(graph, median, edge) candidate_nodes = candidate_nodes.intersection(legal_targets) return candidate_nodes.pop()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

以下は、上記の投稿で使用したサンプルグラフでのスクリプト実行の例です。

 '''        ak bj cfghi dl em ''' G = Graph(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm'], [ ('a', 'b'), ('b', 'c'), ('c', 'd'), ('d', 'e'), ('c', 'f'), ('f', 'g'), ('g', 'h'), ('h', 'i'), ('i', 'j'), ('j', 'k'), ('i', 'l'), ('l', 'm'), ]) def simple_query(v): ans = input("  '%s'  ? [y/N] " % v) if ans and ans.lower()[0] == 'y': return QueryResult(True, None) else: print("     " " '%s'   . : " % v) for w in G.incident_edges: print("%s: %s" % (w, G.incident_edges[w])) target = None while target not in G.vertices: target = input("   '%s': " % v) return QueryResult( False, G.edge(v, target) ) output = binary_search(G, simple_query) print("  : %s" % output)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

クエリ関数は、グラフ構造のリマインダーを表示するだけで、ユーザーに回答（yes / no）を求め、否定的な回答の場合は対応するエッジを報告します。



実行例：



'g' ? [y/N] n

'g' . :

e: [Edge(source='e', target='d', weight=1)]

i: [Edge(source='i', target='h', weight=1), Edge(source='i', target='j', weight=1), Edge(source='i', target='l', weight=1)]

g: [Edge(source='g', target='f', weight=1), Edge(source='g', target='h', weight=1)]

l: [Edge(source='l', target='i', weight=1), Edge(source='l', target='m', weight=1)]

k: [Edge(source='k', target='j', weight=1)]

j: [Edge(source='j', target='i', weight=1), Edge(source='j', target='k', weight=1)]

c: [Edge(source='c', target='b', weight=1), Edge(source='c', target='d', weight=1), Edge(source='c', target='f', weight=1)]

f: [Edge(source='f', target='c', weight=1), Edge(source='f', target='g', weight=1)]

m: [Edge(source='m', target='l', weight=1)]

d: [Edge(source='d', target='c', weight=1), Edge(source='d', target='e', weight=1)]

h: [Edge(source='h', target='g', weight=1), Edge(source='h', target='i', weight=1)]

b: [Edge(source='b', target='a', weight=1), Edge(source='b', target='c', weight=1)]

a: [Edge(source='a', target='b', weight=1)]

'g': f

'c' ? [y/N] n

'c' . :

[...]

'c': d

'd' ? [y/N] n

'd' . :

[...]

'd': e

: e

確率的ストーリー

この投稿で実装したバイナリ検索は非常に最小限です。 実際、同僚とのEmamjome-Zadeの仕事のより興味深い部分は、未知の確率で要求に対する答えが間違っている可能性がある部分です。



この場合、すべての誤った回答に加えて、リクエストに対する正しい回答である多くの最短パスが存在する可能性があります。 特に、これは同じリクエストを数回送信し、最も人気のある回答を選択する戦略を除外します。 エラー率が1/3であり、目的の頂点への最短パスが2つある場合、等しい頻度で3つの回答が表示され、どちらが間違っているかがわからない状況になります。



代わりに、Emamjome-Zade et al。は、乗法の重みを更新するためのアルゴリズムに基づいた手法を使用しています（ 彼は戻ってきました！ ）。 各要求は、要求に対する答えが正しい場合、必要な一定の頂点である多くのノードに対して乗法的増加（または減少）を与えます。 信じられないほどの結果を避けるために、いくつかの詳細と後処理がありますが、一般的には、基本的な考え方は次のとおりです。 この実装は、この最近の記事を深く研究する（または数学の筋肉を伸ばす）ことに興味のある読者にとって、優れた演習となります。



しかし、さらに詳しく見ると、この「結果の改善方法に関するアドバイスの要求と受信」のモデルは、 最初に Dana Engluin によって正式に研究された古典的なトレーニングモデルです。 彼女のモデルでは、分類器を訓練するためのアルゴリズムが設計されています。 有効なクエリは、 所属クエリと等価クエリです。 本質的には、所属は「この要素のラベルは何ですか？」という質問です。また、同等リクエストは「これは有効な分類子ですか？」という形式です。答えが「いいえ」の場合、間違ったラベルの例を送信します。



これは、機械学習の通常の仮定とは異なります。学習アルゴリズムは、ランダムに生成されたデータのサブセットに依存するだけでなく、より多くの情報を取得するサンプルを作成する必要があるためです。 目標は、アルゴリズムが目的の仮説を正確に学習するまで、クエリの数を最小限にすることです。 実際、この投稿で見たように、タスクスペースを調べる時間が少しあれば、多くの情報を受け取るクエリを作成できます。



ここに示されているバイナリグラフ検索モデルは、検索問題における等価クエリの自然な類似物です。間違ったラベルの反例の代わりに、ターゲットに対して正しい方向に「プッシュ」を取得します。 いいね！



ここでは、さまざまな方法で進むことができます：（1）乗法の重みを持つアルゴリズムのバージョンを実装する、（2）この手法をランキングまたはグループ化の問題に適用する、（3）メンバーシップや同等性などの学習の理論モデルをより詳細に検討する