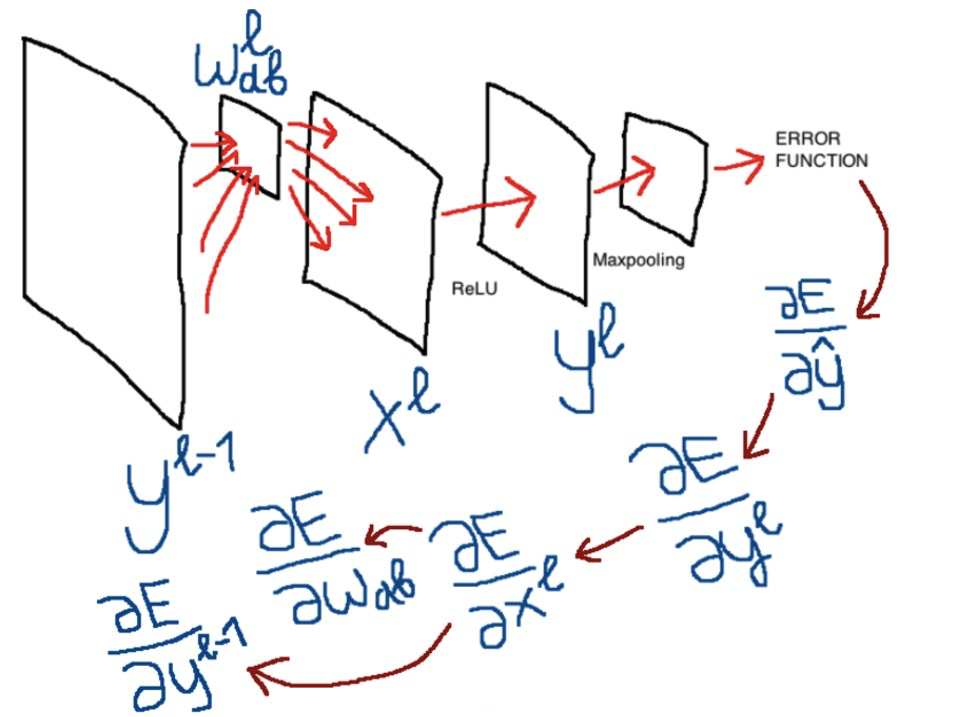
👩🏼‍🤝‍👨🏾 👨‍👨‍👧‍👧 👨🏿‍🎓 Pythonのたたみ込みネットワーク。パート1.モデルの主なパラメーターの決定 😋 🚊 🌉

たたみ込みネットワークでのエラーの逆伝播の方法の原理を説明する記事（1、2、3、4、5、さらには「直感的な」理解-6さえ）を見つけることができるという事実にもかかわらず、私は成功しませんでしたこのトピックを完全に理解します。著者は普通の例に十分な注意を払わないか、または彼らによってよく理解されているが他の人には明らかではないいくつかの機能を省略しており、この理由のすべての資料は耐え難いものになります私は自分のために棚にすべてのものを置きたかったので、その結果、メモは記事になりました。私は既存の説明のすべての欠点を排除しようとしましたが、この記事が質問や誤解を引き起こさないことを願っています。そして、私のように、それを理解したい次の新人は、より少ない時間を費やすでしょう。

この最初の記事では、将来のネットワークのアーキテクチャと、このネットワークを直接通過するためのすべての公式を検討します。 2番目の記事では、エラーの逆伝播について詳しく説明し、式を導き出して分析します。このパートのために、すべてはタスク次第であり、モデルと特に畳み込み層を教えることは私にとって最も難しいと思われました。最後の記事では、Pythonでのネットワーク実装の概観を示し、実際のデータセットでネットワークをトレーニングし、結果を類似の実装と比較しますが、すでにテンソルフローライブラリを使用しています。マテリアル全体を通して、Pythonコードを部分的に投稿して、数式の実装をすぐに確認できるようにします。コードを書くときは、数式を行単位で読みやすくすることに重点を置き、最適化と美しさにかける時間を減らしました。一般的に、最終的な目標は、読者が畳み込みネットワークと完全に接続されたネットワークのパラメーターを更新するすべての複雑さを理解し、このネットワークの作業コードがどのように見えるかを想像できるようにすることです。

これらの記事に含まれないものは何ですか？数学と偏導関数の基礎の説明、逆伝播の本質の「直感的な」理解の詳細（最初にこの優れた記事を読むことができます）、または畳み込みを含む一般的なネットワークの仕組み。素材をよりよく理解するには、これらのこと、特にニューラルネットワークの動作の基礎を知ることが望ましいです。

だから、最初の記事。

畳み込み

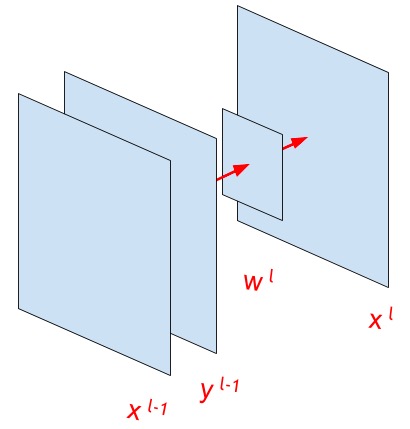
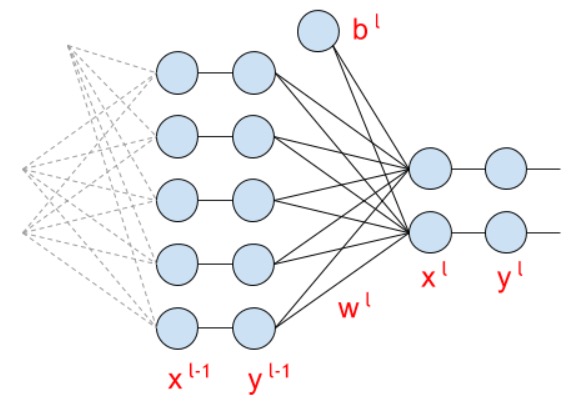
上の図は、これ以降の説明で使用される主な変数を示しています。

畳み込み式を見てみましょう。しかし、最初に、式で何を見たいですか、それは何を反映すべきですか？ウィキペディアを見てみましょう：

「畳み込みニューラルネットワークでは、畳み込み演算は、処理されたレイヤー全体（最初から入力イメージ内で直接）に移動する小さな重量スケールの限られたマトリックスのみを使用し、各シフト後に同じ位置の次のレイヤーニューロンの活性化信号を形成します。つまり、出力層の異なるニューロンに対して、同じ重み行列が使用されます。これは畳み込みカーネルとも呼ばれます...次に、そのような重み行列による畳み込み演算の結果としての次の層は、処理された層とその座標にこの特徴の存在を示し、いわゆる特徴マップを形成します（eng。機能マップ）。」

したがって、畳み込み式はコアの「動き」を示す必要があります

$w ^ l$ 入力画像または特徴マップによる

$y ^ {l-1}$ 。これは、次の式が示すとおりです。

（ ） （ ） （ 、 、 ） （ 、 。 、 ）

$x ^ l_ {ij} = \ sum_ {a =-\ infty} ^ {+ \ infty} \ sum_ {b =-\ infty} ^ {+ \ infty} w ^ l_ {ab} \ cdot y ^ {l -1} _ {（i \ cdot sb）（j \ cdot sb）} + b ^ l \ qquad \ forall i \ in（0、...、N）\ enspace \ forall j \ in（0、.. 。、M）$

下付き文字はこちら

$i$ 、

$j$ 、

$a$ 、

$b$ 行列の要素のインデックスであり、

$s$ -畳み込みステップの値（ストライド）。

上付き

$l$ そして

$l-1$ ネットワーク層のインデックスです。

$x ^ {l-1}$ -以前の機能の出力、またはネットワークの入力画像

$y ^ {l-1}$ あれですか

$x ^ {l-1}$ アクティベーション関数を渡した後（たとえば、reluまたはSigmoid。アクティベーション関数に関する項目は少し後です）

$w ^ l$ -畳み込みコア

$b ^ l$ -バイアスまたはオフセット（上の画像から欠落）

$x ^ l$ 畳み込み演算の結果です。つまり、操作は要素ごとに個別に実行されます

$ij$ 行列

$x ^ l$ その次元

$（N、M）$ 。

以下は、畳み込み式の動作の優れた例です。青で表示

$y ^ {l-1}$ 緑-

$x ^ l$ 、および3×3の灰色の移動行列が畳み込みの中心です

$w ^ l$ ：

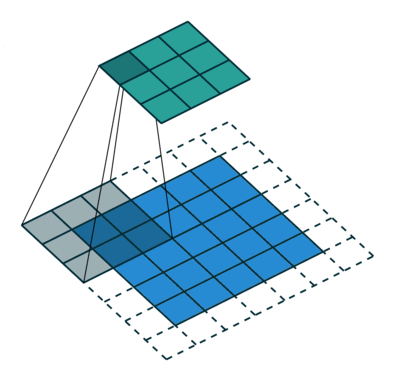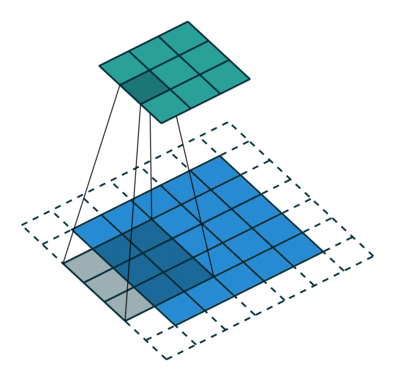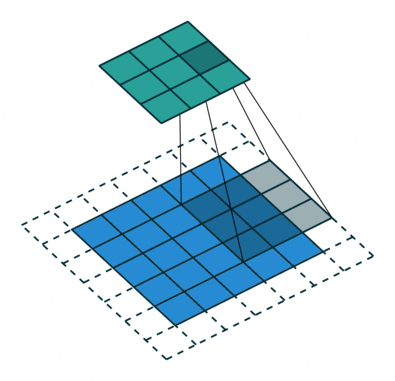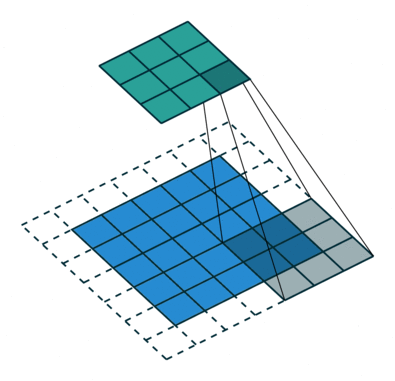
パラメーターの指定を処理し、畳み込み演算の基本原理を理解したら（畳み込み式の詳細は記事の終わりに明らかになるので、後で戻る必要があるかもしれません）、この式と演算自体の重要なニュアンスに進みます：コアには中心的な要素があります。さらに、中心要素は必ずしも中心にあるとは限りません（マトリックスの中心は2 x 2ピクセルですか？）が、一般的にはカーネルの任意のセルで-どんなものでも構いません。たとえば、上記のアニメーションの中心的なコア要素は位置（1,1）にあり、この要素に対して畳み込み演算が発生します。では、中心的な要素は何ですか？

コアコア要素

そのため、カーネルの要素のインデックスは、中心要素の場所に応じて発生します。実際、中心要素は、畳み込みカーネルの「座標軸」の始まりを定義します。下の図を見てください。左側の中央の要素はゼロ行とゼロ列にあり、右側の最初の行と最初の列にはコアがあります。

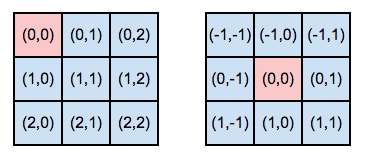
アイテムのインデックス作成がどのように変更されたかをご覧くださいそして、はい、これは最初のコアの番号付けに関して発生したことを念頭に置いて、2番目のコアで中央要素が最初の列の最初の行に「移動」したと言います。実際、中心要素のインデックスは常に等しく（0,0）であり、さらに説明を簡単にするために、左上隅の中心要素の位置と、「新しい」座標-任意の中心要素の位置について、「古い」座標と言います。「古い」座標グリッドの番号付けを使用して、カーネル内の別の場所（たとえば、上の図の右側の畳み込みカーネルの（1,1））。

しかし、畳み込み式に戻ると、それはどういう意味ですか-負の無限大から正の無限大までの合計？結局のところ、コア自体のサイズは非常に明確であり、要素の数は無限ではありません。数式を書くさまざまな方法を見つけました。たとえば、

$\ sum_ {u = -a} ^ {a} \ sum_ {v = -b} ^ {b}$ （あちこちで）。また、記事の冒頭のバージョンのように、無限のオプションを見つけました（こことそこ）。しかし、後者は私にとってより「一般的な」事例のように思えました。

畳み込みカーネルの公式のマイナスは、中心要素の位置の結果です。存在する可能性のあるすべての要素を「整理」する必要があり、マイナスの無限大から始めることができます。またはマイナスから

$a$ そして

$b$ 。これらのインデックスの要素が特定のカーネルに対して定義されていない場合、乗算はゼロで行われ、実際、操作はマイナス無限大からではなく、中央要素の位置からマイナス1を掛けたもの（「古い」座標の番号付け）から始まります。そして、操作は正の無限大ではなく、検討中の軸に沿ったコア要素の数から中心要素のインデックスを引いた差で終了します（再び、「古い」座標軸の番号付けで）。さらに、取得した範囲の最後の値は含まれません（インデックス付けがゼロから行われるため）。

言葉では難しいかもしれませんが、おそらくPythonでどのように実装できるかを確認するのが最善です。以下は、選択した中心要素に応じて、カーネルの「新しい」軸のインデックスを計算するためのコードです。

code_demo_indexes.py

gitリンク

import numpy as np size_axis = (3,3) center_w_l = (1,1) def create_axis_indexes(size_axis, center_w_l): coordinates = [] for i in range(-center_w_l, size_axis-center_w_l): coordinates.append(i) return coordinates def create_indexes(size_axis, center_w_l): #              coordinates_a = create_axis_indexes(size_axis=size_axis[0], center_w_l=center_w_l[0]) coordinates_b = create_axis_indexes(size_axis=size_axis[1], center_w_l=center_w_l[1]) return coordinates_a, coordinates_b print(create_indexes(size_axis, center_w_l))

次の図では、位置（1,1）にある要素のコアの中心を宣言しました。

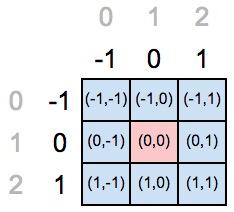
しかし、「古い」座標は、中心要素の位置がインデックス（0,0）にある必要があることを示しています。つまり、中心要素の新しい位置の座標軸を再定義する必要があります。

上記のコードで値を代入すると、範囲（-1、2）の値で満たされたPythonリストが取得されます。つまり、シートには[-1,0,1]が含まれます。もう一度、なぜ範囲（-1、2）ですか？操作は中心要素のマイナスインデックスから始まり、軸の長さ（3に等しい）から古い座標の中心要素のインデックス（つまり1）を引いた値として「2」が取得されるため、「マイナス1」。最後の範囲要素は含まれません。

相互相関

畳み込み式をもう一度説明します。

以下は相互相関式です。

$x ^ l_ {ij} = \ sum_ {a =-\ infty} ^ {+ \ infty} \ sum_ {b =-\ infty} ^ {+ \ infty} w ^ l_ {ab} \ cdot y ^ {l -1} _ {（i \ cdot s + a）（j \ cdot s + b）} + b ^ l$

はい、唯一の違いは下付き文字を計算することの短所です

$y ^ {l-1}$ プラスに置き換えられます。実際には、畳み込み式を使用すると、コアは畳み込み中に「反転」します（さらに、中心要素に対して反転します！）。相互相関の間、コア要素は畳み込み中にその位置を保持します。ここでの意味をよりよく理解するには、図を参照してください。

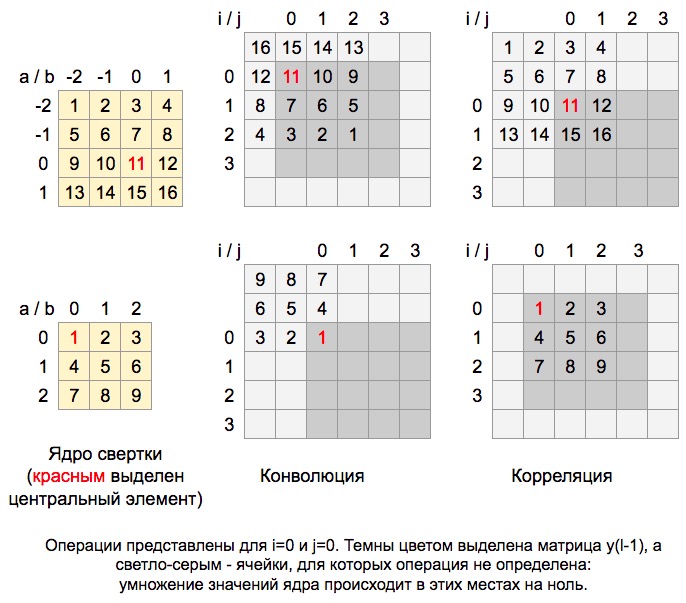
ここで、コアの位置、行列に対する畳み込み中の位置を見ることができます

$y ^ {l-1}$ 。以下は、上の図のデモに似たデモも表示するコードです。

$i$ そして

$j$

code_demo_convolution_feed_x_l.py

gitリンク

 import numpy as np # w_l = np.array([ # [1,2,3,4], # [5,6,7,8], # [9,10,11,12], # [13,14,15,16]]) w_l = np.array([ [1,2], [3,4]]) y_l_minus_1 = np.zeros((3,3)) other_parameters={ 'convolution':True, 'stride':1, 'center_w_l':(0,0) } def convolution_feed_x_l(y_l_minus_1, w_l, conv_params): indexes_a, indexes_b = create_indexes(size_axis=w_l.shape, center_w_l=conv_params['center_w_l']) stride = conv_params['stride'] #          x_l = np.zeros((1,1)) #          if conv_params['convolution']: g = 1 #   else: g = -1 #   #   i  j   y_l_minus_1  ,     x_l    for i in range(y_l_minus_1.shape[0]): for j in range(y_l_minus_1.shape[1]): demo = np.zeros([y_l_minus_1.shape[0], y_l_minus_1.shape[1]]) #     result = 0 element_exists = False for a in indexes_a: for b in indexes_b: # ,        if i*stride - g*a >= 0 and j*stride - g*b >= 0 \ and i*stride - g*a < y_l_minus_1.shape[0] and j*stride - g*b < y_l_minus_1.shape[1]: result += y_l_minus_1[i*stride - g*a][j*stride - g*b] * w_l[indexes_a.index(a)][indexes_b.index(b)] #    ""      w_l demo[i*stride - g*a][j*stride - g*b] = w_l[indexes_a.index(a)][indexes_b.index(b)] element_exists = True #       ,    i  j    if element_exists: if i >= x_l.shape[0]: #  ,    x_l = np.vstack((x_l, np.zeros(x_l.shape[1]))) if j >= x_l.shape[1]: #  ,    x_l = np.hstack((x_l, np.zeros((x_l.shape[0],1)))) x_l[i][j] = result #   demo     print('i=' + str(i) + '; j=' + str(j) + '\n', demo) return x_l def create_axis_indexes(size_axis, center_w_l): coordinates = [] for i in range(-center_w_l, size_axis-center_w_l): coordinates.append(i) return coordinates def create_indexes(size_axis, center_w_l): #              coordinates_a = create_axis_indexes(size_axis=size_axis[0], center_w_l=center_w_l[0]) coordinates_b = create_axis_indexes(size_axis=size_axis[1], center_w_l=center_w_l[1]) return coordinates_a, coordinates_b print(convolution_feed_x_l(y_l_minus_1, w_l, other_parameters))

スクリプト出力の例

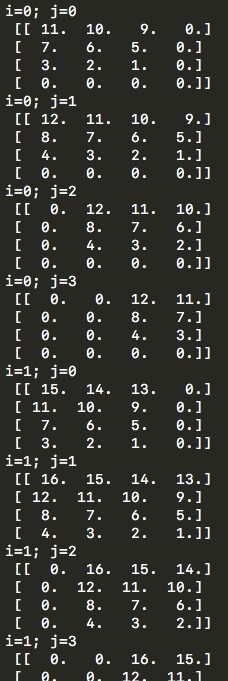
そしてすぐに、中心要素の選択または畳み込みステップの値、カーネル行列の次元、相関または畳み込み式はすべて、これらのニュアンスがエラー伝播式に直接反映されているため、選択されたパラメーターに関係なくトレーニングが正しく実行されることに注意してください。コードでは、これらすべてを実装しようとしました。それらを構成して、すべてを自分で開始してみてください。

畳み込み法（畳み込みまたは相互相関、異なるステップサイズ、中心コア要素の選択）に応じて、出力行列の次元

$x ^ l$ 異なる場合があります。最も単純な場合、ステップが1に等しい場合、行列の次元

$x ^ l$ 行列のそれと等しくなります

$y ^ {l-1}$ 。この次元を見つけるための一般的な式、つまり正確に値

$（N、M）$ 、リストされたすべての機能を考慮して存在します（たとえば、テンソルフローのドキュメントを参照してくださいが、異なるステップサイズの可能性のみが考慮されます）が、上記のPython関数では、行列の次元は最初は

$x ^ l$ 指定されておらず、計算が実行されると行と列がこのマトリックスに追加されますが、これはもちろん最適なソリューションではありません。

アクティベーション機能

以下は、将来のモデルで使用できるアクティベーション関数の公式です。実際、それは単なる「変換」です

$x ^ l$ で

$y ^ l$ このように：

$y ^ l = f（x ^ l）$ 。アクティベーション関数を使用すると、ネットワークを非線形にすることができ、アクティベーション関数を使用しなかった場合（その後、

$y ^ l = x ^ l$ ）または線形関数を使用した場合、ネットワーク内にいくつの層があるかは関係ありません。それらはすべて、線形活性化関数を持つ単一の層に置き換えることができます。

だから、ReLU：

$f_ {ReLU} = max（0、x）$

シグモイド：

$f_ {sigmoid} = \ frac {1} {1 + e ^ {-x}}$

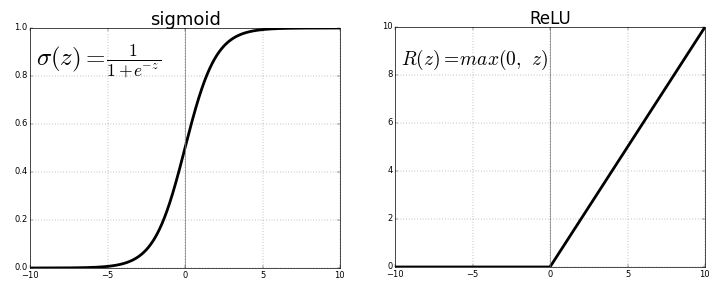
シグモイドは、クラスが2つ以下の場合にのみ使用されます（分類問題の場合）。モデルの出力は、ゼロ（最初のクラス）から1（2番目のクラス）までの数値になります。多数のクラスの場合、モデル出力がこれらのクラスの確率を反映するように（およびネットワーク出力の確率の合計が1に等しくなるように）、softmaxが使用されます。関数は単純に見えますが、backpropの式を計算するのは困難です。

$f_ {softmax} = y ^ l_i = f（x ^ l_i）= \ frac {e ^ {x ^ l_i}} {\ sum_ {k = 0} ^ {n} e ^ {x ^ l_k}}$

どこで

$n$ クラスの数です。

マックスプーリング層

このレイヤーを使用すると、機能マップで重要な機能を強調表示したり、カード上のオブジェクトの検出に不変性を与えたり、カードの寸法を縮小したりしてネットワーク時間を短縮できます。

Python maxpoolingの実装：

code_demo_maxpool.py

gitリンク

 import numpy as np y_l = np.array([ [1,0,2,3], [4,6,6,8], [3,1,1,0], [1,2,2,4]]) other_parameters={ 'convolution':False, 'stride':2, 'center_window':(0,0), 'window_shape':(2,2) } def maxpool(y_l, conv_params): indexes_a, indexes_b = create_indexes(size_axis=conv_params['window_shape'], center_w_l=conv_params['center_window']) stride = conv_params['stride'] #          y_l_mp = np.zeros((1,1)) #  y_l    y_l_mp_to_y_l = np.zeros((1,1), dtype='<U32') #   backprop    (    ) #          if conv_params['convolution']: g = 1 #   else: g = -1 #   #   i  j   y_l  ,        for i in range(y_l.shape[0]): for j in range(y_l.shape[1]): result = -np.inf element_exists = False for a in indexes_a: for b in indexes_b: # ,        if i*stride - g*a >= 0 and j*stride - g*b >= 0 \ and i*stride - g*a < y_l.shape[0] and j*stride - g*b < y_l.shape[1]: if y_l[i*stride - g*a][j*stride - g*b] > result: result = y_l[i*stride - g*a][j*stride - g*b] i_back = i*stride - g*a j_back = j*stride - g*b element_exists = True #       ,    i  j    if element_exists: if i >= y_l_mp.shape[0]: #  ,    y_l_mp = np.vstack((y_l_mp, np.zeros(y_l_mp.shape[1]))) #  y_l_mp_to_y_l    y_l_mp y_l_mp_to_y_l = np.vstack((y_l_mp_to_y_l, np.zeros(y_l_mp_to_y_l.shape[1]))) if j >= y_l_mp.shape[1]: #  ,    y_l_mp = np.hstack((y_l_mp, np.zeros((y_l_mp.shape[0],1)))) y_l_mp_to_y_l = np.hstack((y_l_mp_to_y_l, np.zeros((y_l_mp_to_y_l.shape[0],1)))) y_l_mp[i][j] = result #   y_l_mp_to_y_l   , #          y_l y_l_mp_to_y_l[i][j] = str(i_back) + ',' + str(j_back) return y_l_mp, y_l_mp_to_y_l def create_axis_indexes(size_axis, center_w_l): coordinates = [] for i in range(-center_w_l, size_axis-center_w_l): coordinates.append(i) return coordinates def create_indexes(size_axis, center_w_l): #              coordinates_a = create_axis_indexes(size_axis=size_axis[0], center_w_l=center_w_l[0]) coordinates_b = create_axis_indexes(size_axis=size_axis[1], center_w_l=center_w_l[1]) return coordinates_a, coordinates_b out_maxpooling = maxpool(y_l, other_parameters) print(' :', '\n', out_maxpooling[0]) print('\n', '    backprop:', '\n', out_maxpooling[1])

スクリプト出力の例

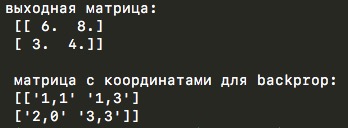
コードは上記の畳み込み関数に非常に似ており、同じパラメーターでさえ保存されています：ストライドの選択、畳み込みのフラグまたは相互相関演算（この関数のロジックに従って、maxpoolウィンドウは畳み込みコアと同一であるため）および中央要素の選択。しかし、もちろん、行列の要素ごとの乗算はありませんが、実際には、特定のウィンドウから最大値を選択するだけです。畳み込みパラメータの最大スプールパラメータの「古典的な」値は、相互相関と左上隅の中央要素の位置です。

デモコードの関数は、2つの行列を返します-小さい次元の出力行列と、最大スプール操作中に元の行列から最大として選択された要素の座標を持つ別の行列です。 2番目のマトリックスは、エラーの逆伝播中に役立ちます。

完全に接続されたネットワーク層

畳み込みの層の後、多くの特徴マップを取得します。それらを1つのベクトルに接続し、このベクトルを完全に接続されたネットワークの入力に送ります。

fcレイヤー（完全に接続された）の式は次のようになります。

$x ^ l_i = \ sum_ {k = 0} ^ {m} w ^ l_ {ki} y ^ {l-1} _k + b ^ l_i \ qquad \ forall i \ in（0、...、n）$

そして、マトリックス形式で（行の下にマトリックスの次元を書きました）：

$X ^ l = Y ^ {l-1} W ^ l + B ^ l_i \\ \ tiny（1 \ times n）\ quad（1 \ times m）（m \ times n）\ quad（1 \ times n ）$

そして、これらの行列が計算中にどのように見えるかは次のとおりです。

$\ begin {aligned} \ begin {bmatrix}＆x ^ {l} _0＆x ^ {l} _1＆x ^ {l} _2＆...＆x ^ {l} _n \ end {bmatrix} = \ begin {bmatrix}＆y ^ {l-1} _0＆y ^ {l-1} _1＆...＆y ^ {l-1} _m \ end {bmatrix} \ begin {bmatrix}＆w ^ {l } _ {00}＆w ^ {l} _ {01}＆...＆w ^ {l} _ {0n} \\＆w ^ {l} _ {10}＆w ^ {l} _ {11 }＆...＆w ^ {l} _ {1n} \\＆...＆...＆...＆... \\＆w ^ {l} _ {m0}＆w ^ {l } _ {m1}＆...＆w ^ {l} _ {mn} \ end {bmatrix} \\ \\ + \ begin {bmatrix}＆b ^ {l} _0＆b ^ {l} _1＆。 ..＆b ^ {l} _n \ end {bmatrix} \ end {aligned}$

損失関数

ネットワークの最終段階は、モデル全体の品質を評価する機能です。損失関数は、ネットワークのすべてのレイヤーの最後にあります。次のようになります。

$E = \ sum_ {i = 0} ^ {n} \ frac {1} {2}（y ^ {truth} _i-y ^ l_i）^ 2$

どこで

$n$ クラスの数です

$y ^ l$ -モデル出力、および

$y ^ {真実}$ -正解。

$\ frac {1} {2}$ ここでは、ネットワークを介したエラーの逆伝播中に式を減らすだけです。取り外せます

$\ frac {1} {2}$ 基本的には何も変わりません。

この記事を読んだ後、クロスエントロピーを使用することにしました。

$E =-\ sum_ {i = 0} ^ {n} y ^ {truth} _iln（y ^ l_i）$

将来のモデルの構造

ネットワークの主要な層を分析したので、将来のモデルの概観を提示できます。

トレーニングのためにデータセットから次の画像/バッチを抽出する機能。
入力で画像を受け取る畳み込みネットワークの最初の層は、出力で機能カードを提供します。
フィーチャマップの次元を削減するmaxpoolingレイヤー。
畳み込みネットワークの2番目の層は、前の手順で取得したカードを受け取り、出力で他の特徴的なカードを提供します。
前の手順で取得したカードを1つのベクターに追加します。
完全に接続されたネットワークの最初のレイヤーはベクトルを取得し、非表示の完全に接続されたレイヤーに値を与える計算を実行します。
完全に接続されたネットワークの2番目の層。その出力ニューロンの数は、使用されるデータセット内のクラスの数と同じです。
モデル全体の出力は損失関数に送られ、予測値と真の値が比較され、これらの値の差が計算されます。

最終損失関数は、定量的な「ペナルティ」の一種であり、予測モデルの品質の尺度と見なすことができます。この値を使用して、backpropagation-エラーの逆伝播を使用してモデルをトレーニングします。このエラーを使用し、すべてのレイヤーで「プル」してパラメーターを更新し、モデルをトレーニングする公式については、記事の次のパートで説明します。

Pythonのたたみ込みネットワーク。 パート1.モデルの主なパラメーターの決定

畳み込み

コアコア要素

相互相関

アクティベーション機能

マックスプーリング層

完全に接続されたネットワーク層

損失関数

将来のモデルの構造

More articles:

Pythonのたたみ込みネットワーク。パート1.モデルの主なパラメーターの決定