任意の関数の補間多項式

はじめに

読者の皆さん、ご挨拶！ 今日、私は次のタスクを検討することを提案します。



与えられた $$$n$ 平面上の点のペア $$$（x_1; y_1）、...、（x_n; y_n）$ 。 全部 $$$x_i$ 違います。 多項式を見つける必要がある $$$M（x）$ そのような $$$M（x_i）= y_i$ どこで $$$i \ in \ {1、...、n \}$



ロシア語への翻訳：Ivan made $$$n$ 平面上のポイント、およびこの情報を持っているメアリーは、（少なくとも）これらすべてのポイントを通過する関数を考え出す必要があります。 現在の記事の枠組みの中で、私たちの仕事はメアリーを回り道で助けることです。



「なぜラウンドアバウトの方法で？」あなたは尋ねます。 答えは伝統的です。この記事は数学に関する一連のアマチュアの記事の続きであり、その目的は数学の世界を普及させることです。

プロセス

そもそも、特定の数の補間多項式が既に存在していることは注目に値します。 これらの多項式は、目的の問題を解決するために設計されたものです。 それらの中で、特にラグランジュおよびニュートン多項式などが知られています。



「任意の関数」とは何かを明確にすることも必要です（この用語は、現在の記事のタイトルに由来します）。 それらは、結果が引数の全単射マッピングである単項関数を意味します。



記事のフレームワークでは、このような関数の10進対数を取ることを提案します $$$\ lg$ そして、次のポイント：

$$

$$（0; 0）\\（1; 1）\\（2; 3）\\（3; 0）$$

飛行機でそれらを表現すると、次のようになります。





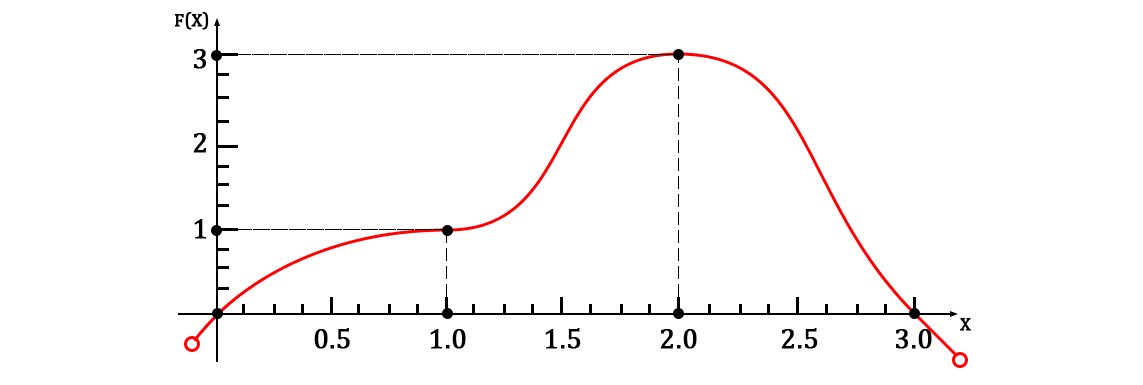
ポイントのペアの数が等しくなったことは簡単にわかります $$$n = 4$ 。



この問題を解決するとき、特定の方程式系が思い浮かびます。ここで、 線形独立線の数は $$$n$ 。 これはどのような連立方程式ですか？



関数を係数付きの10進数の対数の合計として書き込もう（係数の数が $$$n$ ）：

$$

$$f（x）= a \ log（x + 3）+ b \ log（x + 2）+ c \ log（x + 1）+ d$$

の引数 $$$\ lg$ 将来的には文字列の線形依存を避けるために異なります（他のことを考えることができます）。 また、関数の定義の領域が少なくとも $$ （条件で指定されたポイントに基づいて）、関数の値の範囲の存在を確認します $$$\ lg$ この定義の領域で。



知っているから $$$n$ ポイントのペア、次に次の些細なシステムを構築するためにそれらに向かいます：

$$

$$\ begin {cases} \ displaystyle {f（0）= 0 \右矢印a \ lg（3）+ b \ lg（2）+ c \ lg（1）+ d = 0 \\ f（1）= 1 \右矢印a \ lg（4）+ b \ log（3）+ c \ lg（2）+ d = 1 \\ f（2）= 3 \右矢印a \ log（5）+ b \ log（4）+ c \ lg（3）+ d = 3 \\ f（3）= 0 \右矢印a \ lg（6）+ b \ lg（5）+ c \ lg（4）+ d = 0} \ end {cases}$$

システムの自明性は、単にそのようなものを見つけることです $$$a、b、c、d$ 条件のセット全体を満たします。



実際にこのシステムを比較的解く $$$a、b、c、d$ 次の解決策が得られます。

$$

$$\ begin {cases} \ displaystyle {a = \ frac {（5 \ lg ^ 2（2）-5 \ lg（2）\ lg（3）+ \ lg（8/3）\ lg（5））\ log（10）} {3 \ log ^ 3（2）-\ log（9/5）\ log ^ 2（2）+ \ log ^ 2（3）\ log（20）-\ log（2）\ log （5）\ lg（243/5）} \\ b = \ frac {\ lg（675/512）\ lg（2）\ lg（10）} {-3 \ lg ^ 3（2）+ \ lg（ 9/5）\ log ^ 2（2）-\ log ^ 2（3）\ log（20）+ \ log（2）\ log（5）\ log（243/5）} \\ c = \ frac { \ log（10）（2 \ log ^ 2（2）+ \ log（2）（\ log（3）-7 \ log（5））+ \ log（5）\ log（45））} {3 \ log ^ 3（2）-\ log（9/5）\ log ^ 2（2）+ \ log ^ 2（3）\ log（20）-\ log（2）\ log（5）\ log（243 / 5）} \\ d = \ frac {-9 \ log ^ 3（2）+ \ log ^ 2（2）\ log（25/9）+ \ log ^ 2（3）\ log（5）+ \ log （243/125）\ log（2）\ log（3）} {3 \ log ^ 3（2）-\ log（9/5）\ log ^ 2（2）+ \ log ^ 2（3）\ log （20）-\ lg（2）\ lg（5）\ lg（243/5）}} \ end {cases}$$

これで、タスクは自然に終了します。単一の関数に書き込むだけです。

$$

$$f（x）= \ frac {（5 \ log ^ 2（2）-5 \ log（2）\ log（3）+ \ log（8/3）\ log（5））\ log（10）} {3 \ log ^ 3（2）-\ log（9/5）\ log ^ 2（2）+ \ log ^ 2（3）\ log（20）-\ log（2）\ log（5）\ log （243/5）} \ lg（x + 3）\\ + \ frac {\ lg（675/512）\ lg（2）\ lg（10）} {-3 \ lg ^ 3（2）+ \ lg （9/5）\ log ^ 2（2）-\ log ^ 2（3）\ log（20）+ \ log（2）\ log（5）\ log（243/5）} \ log（x + 2 ）\\ + \ frac {\ log（10）（2 \ log ^ 2（2）+ \ log（2）（\ log（3）-7 \ log（5））+ \ log（5）\ log（ 45））} {3 \ log ^ 3（2）-\ log（9/5）\ log ^ 2（2）+ \ log ^ 2（3）\ log（20）-\ log（2）\ log（ 5）\ lg（243/5）} \ log（x + 1）\\ + \ frac {-9 \ log ^ 3（2）+ \ log ^ 2（2）\ log（25/9）+ \ log ^ 2（3）\ log（5）+ \ log（243/125）\ log（2）\ log（3）} {3 \ log ^ 3（2）-\ log（9/5）\ log ^ 2 （2）+ \ log ^ 2（3）\ log（20）-\ log（2）\ log（5）\ log（243/5）}$$

彼女は、もちろん、与えられた一連のポイントを経験します。 関数グラフは次のようになります。





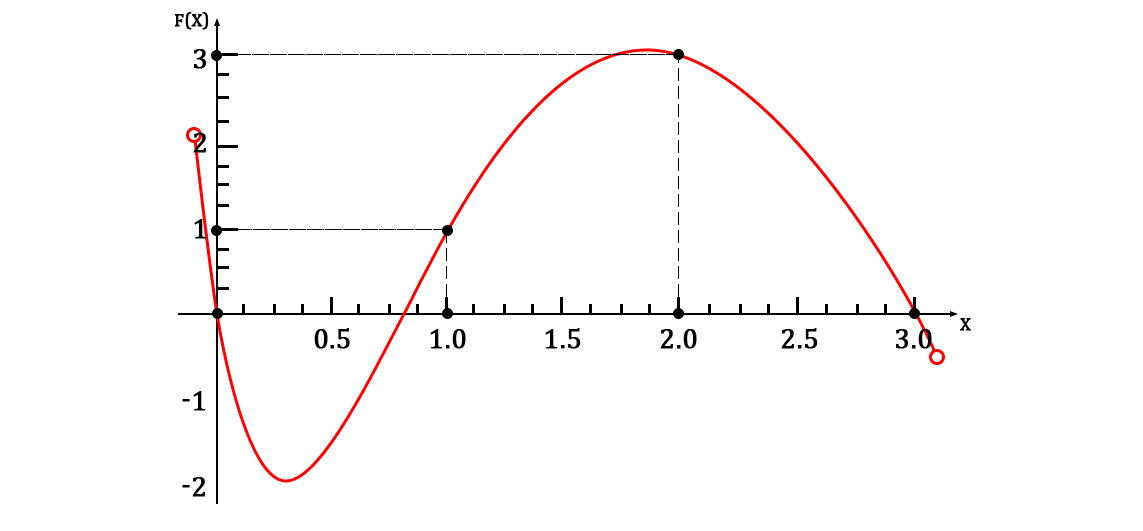
また、明確にするために、近似システムのソリューションを提供できます。

$$

$$\ begin {cases} \ displaystyle {a \およそ-3428.6 \\ b \およそ3789.2 \\ c \およそ-790.20 \\ d \およそ495.22} \ end {cases}$$

その場合、関数の近似形式は次のようになります。

$$

$$f（x）=-3428.6 \ lg（x + 3）+3789.2 \ lg（x + 2）-790.20 \ lg（x + 1）+ 495.22$$

もちろん、結果の関数が最小になるとは誰も言いません（同じラグランジュ多項式はより短い形式を与えます）。 ただし、このメソッドを使用すると、任意の関数のセットを使用して関数を表現できます（ただし、上記の記事で指定された制限に留意してください）。

さまざまな例

デザートについても、同様にラジカルで関数を構築します：

$$

$$f（x）= ax ^ 3 + bx ^ 2 + cx + d$$

係数を見つけるための方程式系を構成します。

$$

$$\ begin {cases} \ displaystyle {f（0）= 0 \ Rightarrow d = 0 \\ f（1）= 1 \ Rightarrow a + b + c + d = 1 \\ f（2）= 3 \ Rightarrow 8a + 4b + 2c + d = 3 \\ f（3）= 0 \ Rightarrow 27a + 9b + 3c + d = 0} \ end {cases}$$

彼女のソリューションはユニークで、次のように見えます。

$$

$$\ begin {cases} \ displaystyle {a = -1 \\ b = \ frac {7} {2} \\ c =-\ frac {3} {2} \\ d = 0} \ end {cases}$$

完成した関数は次のとおりです。

$$

$$f（x）=-x ^ 3 + \ frac {7} {2} x ^ 2- \ frac {3} {2} x$$

組み合わせて、与えられたポイントのセットのラグランジュ多項式です（記事のアルゴリズムのラジカル形式を暗黙的に実装しているため）。 与えられた点の面積のグラフは次のようになります。







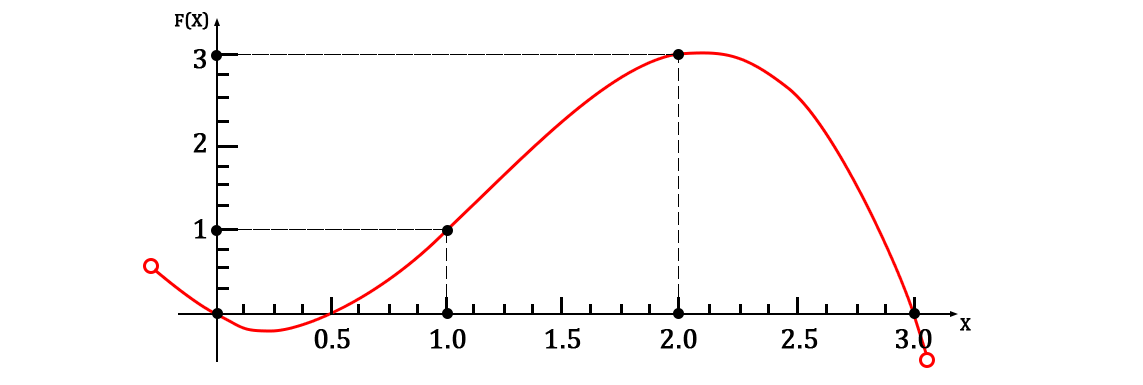
このストーリーで最も興味深いのは、有限関数を構築するための任意の関数を組み合わせることができることです。 言い換えると、関数は、ラジカルと対数、または他の何か（指数関数、階乗など）ですぐに構築できます。 取得した関数のセットのみが、係数の選択において行の線形独立性を提供した場合。 一般的な形式で $$$n$ 次のようなポイントのペア：

$$

$$f（x）= a_1 * g_1（x）+ ... + a_n * g_n（x）$$

どこで $$$a_1、..、a_n$ -連立方程式（SLAE）で求められる係数、および $$$g_1、...、g_n$ -係数を見つける際に線形独立性を提供するいくつかの関数。



そして-上記のアルゴリズムによれば、すべてがまったく同じです。 忘れないで $$$g_1、...、g_n$ 条件付きで指定されたポイントで定義する必要があります。



たとえば、まったく異なる基本関数で構成される関数を表示できます。

$$

$$f（x）= ax ^ 2 + b2 ^ x + cx + d$$

与えられたポイントのセットを満たすために、係数は次のようになります（記事のアルゴリズムに従って厳密に見つけられます）。

$$

$$\ begin {cases} \ displaystyle {a = \ frac {7} {2} \\ b = -6 \\ c = \ frac {7} {2} \\ d = 6} \ end {cases}$$

そして、関数自体は次のようになります。

$$

$$f（x）= \ frac {7} {2} x ^ 2-6 * 2 ^ x + \ frac {7} {2} x + 6$$

グラフは、前のグラフとほぼ同じように見えます（指定されたポイントの領域）。

より「スムーズな」スケジュールが必要な場合は、次のように階乗形式の方向を見ることができます。

$$

$$f（x）= a（x + 2）！+ b（x + 1）！+ cx！+ d$$

係数を見つける：

$$ $$ display $$ \ begin {cases} \ displaystyle {2a + b + c + d = 0 \\ 6a + 2b + c + d = 1 \\ 24a + 6b + 2c + d = 3 \\ 120a + 24b + 6c + d = 0} \ end {cases} \ Rightarrow \ begin {cases} \ displaystyle {a = -13/16 \\ b = 17/4 \\ c = -3/8 \\ d = -9/4 } \ end {cases} $$ディスプレイ$$

完成した関数でこれらを置き換えます：

$$

$$f（x）=-\ frac {13} {16}（x + 2）！+ \ frac {17} {4}（x + 1）！-\ frac {3} {8} x！-\ frac {9} {4}$$

また、非常に良いスケジュールをお楽しみください：

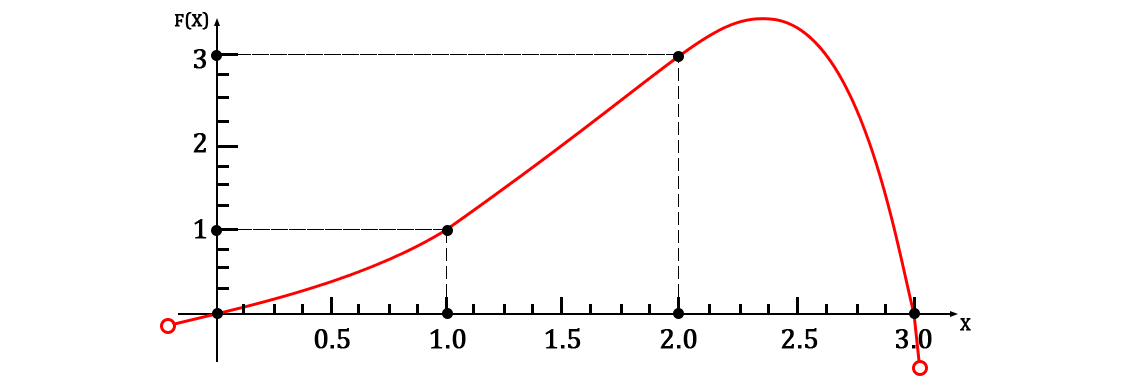
なぜこれが必要なのですか？

はい、少なくともプラスチック製のクランプで引っ張られたロープの束を想像するために:)



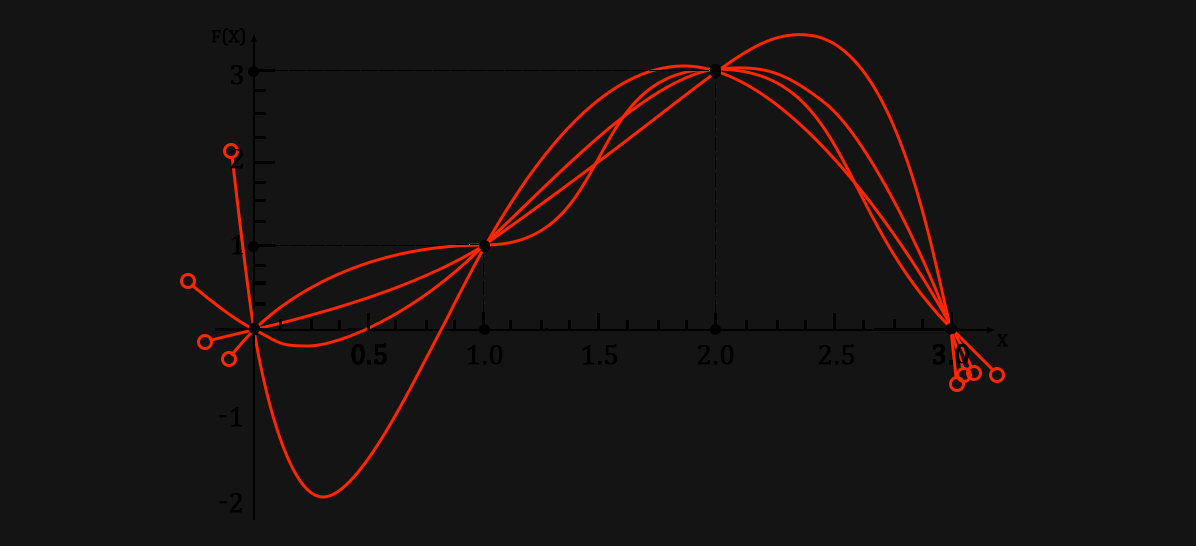
（ *ここでは、すべてのチャートを重ねて表示しています ）



これがすべて現在の記事にあります。自分でプレイすることをお勧めします。



最高の

ピーターはあなたと一緒でした。